PCL：从法线计算到曲率计算并可视化

----------------法线求解原理--------------

表面法线是几何体表面的重要属性，在很多领域都有大量应用，例如：在进行光照渲染时产生符合可视习惯的效果时需要表面法线信息才能正常进行，对于一个已知的几何体表面，根据垂直于点表面的矢量，因此推断表面某一点的法线方向通常比较简单。然而，由于我们获取的点云数据集在真实物体的表面表现为一组定点样本，这样就会有两种解决方法：

（1）使用曲面重建技术，从获取的点云数据集中得到采样点对应的曲面，然后从曲面模型中计算表面法线；曲面方程f(x,y,z)=0的一个法向量可以表示为n={e(df/dx), e(df/dy), e(df/dz)}.）

（2）直接从点云数据集中近似推断表面法线。

下面以已知一个点云数据集，在其中的每个点处直接近似计算表面法线。为例进行展开：

确定表面一点法线的问题近似于估计表面的一个相切面法线的问题，因此转换过来以后就变成一个最小二乘法平面拟合估计问题。

最小二乘法（又称最小平方法）是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据，并使得这些求得的数据与实际数据之间误差的平方和为最小。最小二乘法还可用于曲线拟合。其他一些优化问题也可通过最小化能量或最大化熵用最小二乘法来表达。

对空间中的一系列散点，寻求一个近似平面：（按最小原则选择的拟合平面为最小二乘拟合平面）

上述使用最小二乘我们已经可以根据某点的临近点阈，可以拟合出一个平面。接下来就是求平面的法线。表面法线是几何体面的重要属性。而点云数据集在真实物体的表面表现为一组定点样本。对点云数据集的每个点的法线估计，可以看作是对表面法线的近似推断。在PCL库中有专门针对法向量计算的库，但是必须了解计算原理才能记得更加深刻。

确定表面一点法线的问题近似于估计表面的一个相切面法线的问题，因此转换过来以后就变成一个最小二乘法平面拟合估计问题。

下一张图说明怎么是由求法线转换到求最小特征值对应的特征向量就是代表法线。

类似于上图中的平面方程求解，只是换了一种平面表示方法。（由一般式转换为法线式方程）

  

由上述推导过程可知，求法线就是求最小特征值对应的特征向量。

----

还可以观察上述右边图片中的A矩阵其实是个协方差矩阵；

在PCL内估计一点集对应的协方差矩阵，可以使用以下函数调用实现：

//定义每个表面小块的3x3协方差矩阵的存储对象
Eigen::Matrix3fcovariance_matrix;
//定义一个表面小块的质心坐标16-字节对齐存储对象
Eigen::Vector4fxyz_centroid;
//估计质心坐标
compute3DCentroid(cloud,xyz_centroid);
//计算3x3协方差矩阵
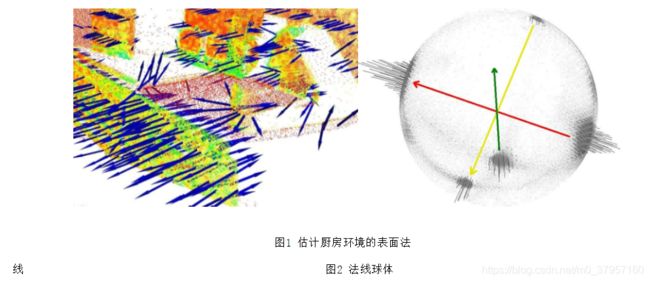
computeCovarianceMatrix(cloud,xyz_centroid,covariance_matrix);

通常，没有数学方法能解决法线的正负向问题，如上所示，通过主成分分析法（PCA）来计算它的方向也具有二义性，无法对整个点云数据集的法线方向进行一致性定向。图1显示出对一个更大数据集的两部分产生的影响，此数据集来自于厨房环境的一部分，很明显估计的法线方向并非完全一致，图2展现了其对应扩展的高斯图像（EGI），也称为法线球体（normal sphere），它描述了点云中所有法线的方向。由于数据集是2.5维，其只从一个单一的视角获得，因此法线应该仅呈现出一半球体的扩展高斯图像（EGI）。然而，由于定向的不一致性，它们遍布整个球体，如图2所示。

如果实际知道视点，那么这个问题的解决是非常简单的。对所有法线定向只需要使它们一致朝向视点方向，满足下面的方程式：

                                             

下面的图3展现了上面图1中的数据集的所有法线被一致定向到视点后的结果演示。

在PCL中对一个已知点的法线进行手动重新定向，你可以使用：

flipNormalTowardsViewpoint (const PointT &point, float vp_x, float vp_y, float vp_z, Eigen::Vector4f &normal);

注意：如果数据集是从多个捕获视点中配准后集成的，那么上述法线的一致性定向方法就不适用了。需要使用更复杂的算法。更详细的信息见：http://pointclouds.org/documentation/tutorials/how_features_work.php#id1

选择合适的尺度

如之前介绍的，在估计一个点的表面法线时，我们需要从周围支持这个点的邻近点着手（也称作k邻域）。最近邻估计问题的具体内容又提出了另一个问题“合适的尺度”：已知一个取样点云数据集，k的正确取值是多少（k通过pcl::Feature::setKSearch给出）或者确定一个点r为半径的圆内的最近邻元素集时使用的半径r应该取什么值（r通过pcl::Feature::setRadiusSearch给出）。这个问题非常重要，并且在一个点特征算子的自动估计时（例如：用户没有给定阈值）是一个限制因素。为了更好地说明这个问题，以下图示表现了选择更小尺度（如：r值或k取相对小）与选择更大尺度（如：r值或k值比较大）时的两种不同效果。图4和图5分别为近视图和远视图，两图中左边部分展示选择了一个合理的比例因子，估计的表面法线近似垂直于两个平面，即使在互相垂直的边沿部分，可明显看到边沿。如果这个尺度取的太大（右边部分），这样邻近点集将更大范围地覆盖邻近表面的点，估计的点特征表现就会扭曲失真，在两个平面边缘处出现旋转表面法线，以及模糊不清的边界，这样就隐藏了一些细节信息。

无法深入探究更多讨论，现在可粗略假设，以应用程序所需的细节需求为参考，选择确定点的邻域所用的尺度。简言之，如果杯子手柄和圆柱体部分之间边缘的曲率是重要的，那么需要足够小的尺度来捕获这些细节信息，而在其他不需要细节信息的应用中可选择大的尺度。

估计法线实例详解：http://pointclouds.org/documentation/tutorials/index.php#features-tutorial

法线估计类NormalEstimation的实际计算调用程序内部执行以下操作：

对点云P中的每个点p
  1.得到p点的最近邻元素
  2.计算p点的表面法线n
  3.检查n的方向是否一致指向视点，如果不是则翻转

视点坐标默认为（0,0,0），可以使用以下代码进行更换：

setViewPoint (float vpx, float vpy, float vpz);

计算单个点的法线，使用：

computePointNormal (const pcl::PointCloud&cloud, const std::vector&indices, Eigen::Vector4f &plane_parameters, float&curvature);

此处，cloud是包含点的输入点云，indices是点的k-最近邻元素集索引，plane_parameters和curvature是法线估计的输出，plane_parameters前三个坐标中，以(nx, ny, nz)来表示法线，第四个坐标D = nc . p_plane (centroid here) + p。输出表面曲率curvature通过协方差矩阵的特征值之间的运算估计得到，如：

                                    

使用OpenMP加速法线估计

对于对运算速度有要求的用户，PCL点云库提供了一个表面法线的附加实现程序，它使用多核/多线程开发规范，利用OpenMP来提高计算速度。它的类命名为pcl::NormaleEstimationOMP，并且它的应用程序接口（API）100%兼容单线程pcl::NormalEstimation，这使它适合作为一个可选提速方法。在8核系统中，可以轻松提速6-8倍。

-------------------曲率求解-----------------

曲率大小反映模型表面的凹凸程度。

利用上面法向量估计的PCA方法，在法向量估算的基础上进行数据点的曲率估算，曲率的估算方法如上式：

入描述了曲面沿法向量的变化，而和表示数据点在切平面上的分布情况。定义下式为数据点，在k邻域内的曲面变分。

                                            

点云模型在数据点的曲率可近似为在该点的曲面变分,即。

该式的基本思想实际上是使用曲面变分来近似曲率信息[1]。

曲率基础知识：
平均曲率、主曲率和高斯曲率是曲率的三个基本要素。
法曲率：曲面在一点沿着不同方向的弯曲程度不同。或者说曲面离开切平面的速度不同。这个弯曲属性可以用这一点的沿着这个方法的法曲率刻画
主曲率：过曲面上某个点上具有无穷个正交曲率，其中存在一条曲线使得该曲线的曲率为极大，这个曲率为极大值Kmax，垂直于极大曲率面的曲率为极小值Kmin。这两个曲率属性为主曲率。他们代表着法曲率的极值。
平均曲率：是空间上曲面上某一点任意两个相互垂直的正交曲率的平均值。如果一组相互垂直的正交曲率可表示为K1,K2,那么平均曲率则为：K = (K1 +K2 ) / 2。
高斯曲率：两个主曲率的乘积即为高斯曲率，又称总曲率，反映某点上总的完全程度。

#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;

int main (int argc, char** argv){

  pcl::PointCloud::Ptr cloud (new pcl::PointCloud);
  pcl::io::loadPCDFile("A3  - Cloud.pcd", *cloud); //读取点云
  cout << "Loaded " << cloud->points.size() << " points." << std::endl;//显示读取点云的点数
  // 计算点云的法线
  pcl::NormalEstimation normalEstimation;
  normalEstimation.setInputCloud (cloud);
  //设置邻域点搜索方式
  pcl::search::KdTree::Ptr tree (new pcl::search::KdTree);
  normalEstimation.setSearchMethod (tree);
  //定义一个新的点云储存含有法线的值
  pcl::PointCloud::Ptr cloudWithNormals (new pcl::PointCloud);
  //设置KD树搜索半径
 // normalEstimation.setRadiusSearch (0.03);
  normalEstimation.setKSearch(10);
  //计算出来法线的值
  normalEstimation.compute (*cloudWithNormals);
  // 建立主曲率计算
  pcl::PrincipalCurvaturesEstimation principalCurvaturesEstimation;
  // 提供原始点云(没有法线)
  principalCurvaturesEstimation.setInputCloud (cloud);
  // 为点云提供法线
  principalCurvaturesEstimation.setInputNormals(cloudWithNormals);
  // 使用与法线估算相同的KdTree
  principalCurvaturesEstimation.setSearchMethod (tree);
  //principalCurvaturesEstimation.setRadiusSearch(1.0);
  principalCurvaturesEstimation.setKSearch(10);
  // 计算主曲率
  pcl::PointCloud::Ptr principalCurvatures (new pcl::PointCloud ());
  principalCurvaturesEstimation.compute (*principalCurvatures);
  std::cout << "output points.size: " << principalCurvatures->points.size () << std::endl;
  // 显示和检索第0点的主曲率。
  cout << "最大曲率;"<< principalCurvatures->points[0].pc1 << endl;//输出最大曲率
  cout << "最小曲率:"<< principalCurvatures->points[0].pc2 << endl;//输出最小曲率
  //输出主曲率方向（最大特征值对应的特征向量）
  cout << "主曲率方向;" << endl;
  cout << principalCurvatures->points[0].principal_curvature_x << endl;
  cout << principalCurvatures->points[0].principal_curvature_y << endl;
  cout << principalCurvatures->points[0].principal_curvature_z << endl;

  return 0;
}

[1]