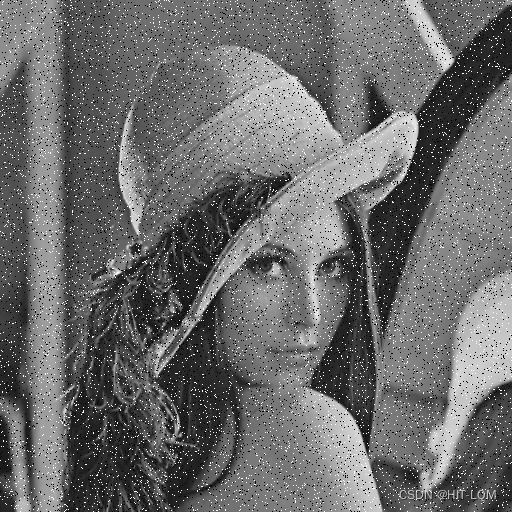计算机视觉 基础算法之噪声、滤波
作为CV初学者,日常记录一些学到的小知识
一、噪声
什么是噪声呢?
图像噪声是图像在摄取或传输时所受的随机信号干扰,是图像中各种妨碍人们对其信息接受的因素。很多时候将图像噪声看成是多维随机过程,因而描述噪声的方法完全可以借用随机过程的描述,即用其概率分布函数和概率密度分布函数。图像噪声是多种多样的,其性质也千差万别,所以了解噪声的分类是很有必要的。
常见的噪声包括椒盐噪声、高斯噪声等等。
1.椒盐噪声
椒盐噪声,即在图片中的像素随机出现一些白色或者黑色点,对图片的信息造成了干扰。
当图像中出现椒盐噪声时,可使用中值滤波处理。
void addSaltNoise(const cv::Mat &srcImage, cv::Mat &dstImage, int n) {
dstImage = srcImage.clone();
//拷贝一个原始图像的副本
for (int k = 0; k < n; k++) {
// 随机取值行列产生椒盐
int i = rand() % dstImage.rows;
int j = rand() % dstImage.cols;
if (dstImage.channels() == 1)
{
// 图像通道判定
dstImage.at(i, j) = 255;
} else {
// 访问三个通道
dstImage.at(i, j)[0] = 255;
dstImage.at(i, j)[1] = 255;
dstImage.at(i, j)[2] = 255;
}
}
for (int k = 0; k < n; k++) {
int i = rand() % dstImage.rows;
int j = rand() % dstImage.cols;
if (dstImage.channels() == 1) {
dstImage.at(i, j) = 0;
} else {
dstImage.at(i, j)[0] = 0;
dstImage.at(i, j)[1] = 0;
dstImage.at(i, j)[2] = 0;
}
}
//保存到文件夹
cv::imwrite("../img-1 and img-2/Salt_and_pepper_noise.jpeg", dstImage);
} 效果如下
2.高斯噪声
高斯噪声是指它的概率密度函数服从高斯分布(即正态分布)的一类噪声。
与椒盐噪声相似(Salt And Pepper Noise),高斯噪声(gauss noise)也是数字图像的一个常见噪声。
椒盐噪声是出现在随机位置、噪点深度基本固定的噪声,高斯噪声与其相反,是几乎每个点上都出现噪声、噪点深度随机的噪声。
通过概率论里关于正态分布的有关知识可以很简单的得到其计算方法,高斯噪声的概率密度服从高斯分布(正态分布)其中有means(平均值)和sigma(标准方差)两个参数。
对于每个输入像素,我们可以通过与符合高斯分布的随机数相加, 得到输出像素:
/**
* @brief 生成高斯随机变量
* @param[in] mean 均值
* @param[in] variance 方差
* @return double 生成的随机变量
* @author HITSteven ([email protected])
*/
double addGaussianNoiseParameter(double mean, double variance) {
const double epsilon = std::numeric_limits::min();
static double z0, z1;
static bool flag = false;
flag = !flag;
// 构造高斯随机变量
if (!flag) return z1 * variance + mean;
double u1, u2;
do {
u1 = rand() * (1.0 / RAND_MAX);
u2 = rand() * (1.0 / RAND_MAX);
} while (u1 <= epsilon);
z0 = sqrt(-2.0 * log(u1)) * cos(2 * CV_PI * u2);
z1 = sqrt(-2.0 * log(u1)) * sin(2 * CV_PI * u2);
return z0 * variance + mean;
} 随后可以利用上述函数对图片添加高斯噪声
/**
* @brief 添加高斯噪声
* @param[in] srcImage 原始图片
* @param[in] dstImage 生成图片
* @param[in] mean 均值
* @param[in] variance 方差
* @author HITSteven ([email protected])
*/
void addGaussianNoise(cv::Mat &srcImage, cv::Mat &dstImage, double mean, double variance) {
//拷贝图片副本
dstImage = srcImage.clone();
//获取通道数,行数,列数
int channels = dstImage.channels();
int rowsNumber = dstImage.rows;
int colsNumber = dstImage.cols * channels;
// 判断图像的连续性
if (dstImage.isContinuous()) {
colsNumber *= rowsNumber;
rowsNumber = 1;
}
for (int i = 0; i < rowsNumber; i++) {
for (int j = 0; j < colsNumber; j++) {
// 加入高斯噪声
int val = dstImage.ptr(i)[j] + addGaussianNoiseParameter(mean, variance) * 32;//利用上述的高斯随机变量函数
if (val < 0) val = 0;
if (val > 255) val = 255;
dstImage.ptr(i)[j] = (uchar)val;
}
}
//将文件写入文件夹
cv::imwrite("../img-1 and img-2/Gaussian_Noise.jpeg", dstImage);
} 效果如下
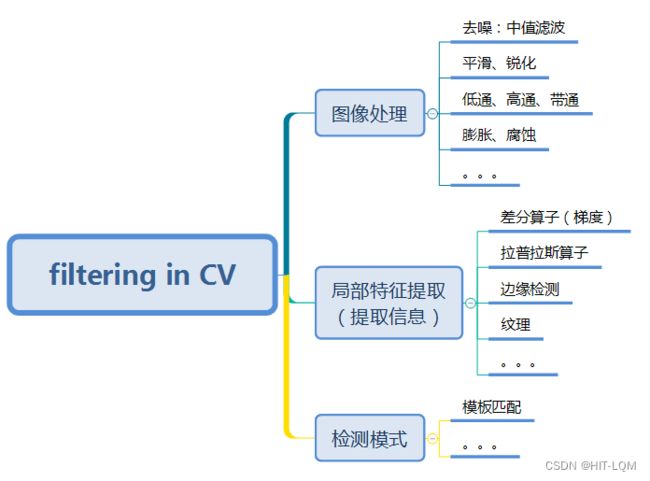
二、常见的滤波
在计算机视觉中,滤波(filtering)是指一种特殊的函数,其作用在图像的每个位置,通过定义的计算方式得到输出,输出的值用于替换图像当前位置(滤波器中心)的值。
令滤波函数为g ( x ; w ) ,其中x 为图像的局部邻域,w 为滤波器的权重,滤波器可以分成如下3类,
线性滤波器(Linear filter):线性滤波的输出为输入的线性组合,即g = w ⋅ x ,线性滤波器最为常见;
非线性滤波器(Non-Linear Filter):不满足上条性质的为非线性滤波,典型的非线性滤波如最大值/最小值/中值滤波、膨胀/腐蚀等;
自适应滤波器(Adaptive filter):线性滤波中的w在滑动过程中固定不变(与图像内容独立无关),自适应滤波的w在滑动过程中会随着窗口内像素的性质和结构发生变化。直觉上,自适应滤波器在某些复杂情况下可能取得更好的效果,但相对线性滤波器,其计算代价更高也更难优化加速。
从滤波目的或者解决的问题上,也可分成3类:
Padding
滤波操作不可避免的一个问题是边界如何处理,当滤波器的中心压在图像边界处时,滤波器会有一部分落在图像外,但图像外并没有像素,该如何处理?通常需要对图像进行填充(padding),填充需要解决2个问题,填充的元素取什么值以及填充多少个元素。
对于延拓元素的取值,通常有4种方式,
常数填充(0填充):填充的元素取相同的常数值
周期填充(circular):认为图像的上下左右被与自身相同的图像包围着
复制填充(replicate):复制图像边界的元素
对称填充(symmetric):填充的元素与图像关于边界对称
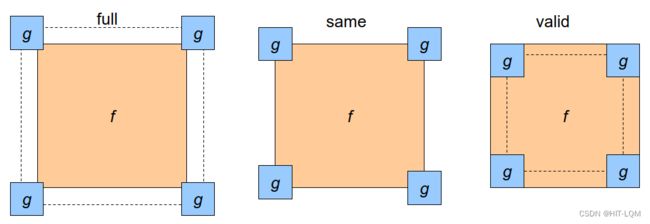
4种填充方式依次如下图所示,
对于填充多少个元素,通常有3种方式,令滤波器的大小为g*g,图像大小为f × f 。
滤波杂谈
1.基本假设:局部相关性(远处无关)、局部相似(edge处不满足)、噪声随机2.静止图像的去噪,若能获得图像序列,可以在时域上滤波(均值、中值等);单张图像在空域上滤波。
3.椒盐噪声用中值滤波。椒盐噪声会随机地将像素置为黑或白,在实践中,会大幅改变像素值的噪声一般采用中值滤波都是有效的。
4.非椒盐噪声,均值为0的随机噪声(高斯噪声),可通过moving average滤波。
5.与图像内容耦合的噪声,可能需要依赖先验知识,采用合适的自适应滤波器,更多内容可以查看参考链接。
6.平滑相当于低通、锐化相当于高通、不同平滑半径的差相当于带通。
7.滤波的加速可以考虑:滤波器是否行列可分离、缓存不必要的重复计算、近似计算、SIMD等。
8.差分算子对噪声敏感,所以差分前通常要先平滑。考虑到噪声,求梯度前通常要先(高斯)平滑再使用差分算子,sobel算子可以看成是DoG(Derivative of Gaussian)的近似,可以拆分成平滑和差分。
9.模式检测需要根据期望探测的模式来定义filter,因为不同场景需要检测的模式不同,所以filter也多种多样。反映模式的filter可以根据领域知识来人工定义、可以通过SOM(Self Organizing Map)无监督生成、也可以像CNN那样通过数据驱动有监督学习得到。比如,模板匹配中的模板为filter,相似度函数为滤波的计算方法;稀疏表示中字典的每一列都是filter,像gabor小波字典,通过相关运算计算与每个filter的相似程度,从而知道每个图像局部“长什么样子”。
常见的几种滤波的代码实现
1.中值滤波
/**
* @brief 添加中值滤波处理
* @param[in] srcImage 原始图片
* @param[in] dstImage 处理后得到的图片
* @author HITSteven ([email protected])
*/
void MedianFilter(const cv::Mat &srcImage, cv::Mat &dstImage) {
std::vector grayv(9);
cv::Mat grayImage;
// 生成灰度图,将RGB转换为灰度图片
cv::cvtColor(srcImage, grayImage, cv::COLOR_RGB2GRAY);
dstImage = grayImage.clone();//拷贝图片
for (int i = 1; i < grayImage.rows - 1; i++) {
uchar *preptr = grayImage.ptr(i - 1); // 改变像坐标点像素
uchar *ptr = grayImage.ptr(i);
uchar *nextptr = grayImage.ptr(i + 1);
uchar *imgptr = dstImage.ptr(i);
for (int j = 1; j < grayImage.cols - 1; j++) {
// 遍历邻域像素
grayv[0] = (preptr[j - 1]);
grayv[1] = (preptr[j]);
grayv[2] = (preptr[j + 1]);
grayv[3] = (ptr[j - 1]);
grayv[4] = (ptr[j]);
grayv[5] = (ptr[j + 1]);
grayv[6] = (nextptr[j - 1]);
grayv[7] = (nextptr[j]);
grayv[8] = (nextptr[j + 1]);
// 排序并选取中值
std::sort(grayv.begin(), grayv.end());
imgptr[j] = int(grayv[4]);
}
}
} 效果如下
分别处理椒盐噪声和高斯噪声
2.均值滤波
/**
* @brief 添加均值滤波
* @param[in] src 原始图像
* @param[in] dst 处理后图像
* @author HITSteven ([email protected])
*/
void MeanFilter(const cv::Mat &src, cv::Mat &dst, cv::Size wsize) {
// 判断原图像是否为空
if (src.empty()) {
return;
}
//判断矩阵的行列数为奇数
if (wsize.height % 2 == 0 || wsize.width % 2 == 0) {
fprintf(stderr, "Please enter odd size!");
exit(-1);
}
int hh = (wsize.height - 1) / 2;
int hw = (wsize.width - 1) / 2;
cv::Mat Newsrc;
copyMakeBorder(src, Newsrc, hh, hh, hw, hw, cv::BORDER_REFLECT_101);//以边缘为轴,对称
dst = cv::Mat::zeros(src.size(), src.type());
// 三通道彩色图片处理
if (Newsrc.channels() == 3) {
//int q = 0;//test
// 定义每个通道的核的总数和平均值,并置0
int sumR = 0, sumG = 0, sumB = 0;
int averageR = 0, averageG = 0, averageB = 0;
for (int i = hh; i < src.rows + hh; i++)
for (int j = hw; j < src.cols + hw; j++) {
for (int r = i - hh; r <= i + hh; r++) {
cv::Vec3b * data_New = Newsrc.ptr(r);
// 求核的总数
for (int k = j - hh; k <= j + hh; k++) {
sumR += data_New[k][0];
sumG += data_New[k][1];
sumB += data_New[k][2];
}
}
// 求平均数
averageR = sumR / (wsize.area());
averageG = sumG / (wsize.area());
averageB = sumB / (wsize.area());
// 写入目标图像
cv::Vec3b* dataDst = dst.ptr(i - hh);
dataDst[j - hw][0] = averageR;
dataDst[j - hw][1] = averageG;
dataDst[j - hw][2] = averageB;
// 总和和平均数置0
sumR = 0; sumG = 0; sumB = 0;
averageR = 0; averageG = 0; averageB = 0;
}
}
// 单通道图片处理
else if (Newsrc.channels() == 1) {
int sum = 0;
int average = 0;
for (int i = hh; i < src.rows + hh; i++) {
for (int j = hw; j < src.cols + hw; j++) {
for (int r = i - hh; r <= i + hh; r++) {
uchar* data = Newsrc.ptr(r);
for (int k = j - hh; k <= j + hh; k++) {
sum += data[k];
}
}
average = sum / (wsize.area());
uchar* data_dst = dst.ptr(i - hh);
data_dst[j - hw] = average;
sum = 0;
average = 0;
}
}
}
else
{
return;
}
}
效果如下
分别处理椒盐噪声和高斯噪声
3.高斯滤波
生成高斯核
double **GetGaussianKernel(int size, double sigma) {
double sum = 0.0;
int center = size / 2; // 用于计算中心点的坐标
double **arr = new double *[size];
for (int i = 0; i < size; ++i) {
arr[i] = new double[size];
}
for (int i = 0; i < size; ++i) {
for (int j = 0; j < size; ++j) {
arr[i][j] =
exp(-((i - center) * (i - center) + (j - center) * (j - center)) / (2 * sigma * sigma));
sum += arr[i][j];
}
}
for (int i = 0; i < size; ++i) {
for (int j = 0; j < size; ++j) {
// 得到权重二维数组
arr[i][j] /= sum;
}
}
return arr;
}高斯滤波
void GaussianBlur(const cv::Mat &srcImage, cv::Mat &dstImage, int size, double sigma) {
cv::Mat img = srcImage.clone();
cv::Mat dst(img.size(), img.type(), cv::Scalar::all(0));
double **gaus = GetGaussianKernel(size, sigma);
int center = size / 2;
// 扩展边界
cv::copyMakeBorder(img, img, center, center, center, center, cv::BORDER_REPLICATE);
for (int i = center; i < img.rows - center; ++i) {
for (int j = center; j < img.cols - center; ++j) {
for (int x = -center; x <= center; ++x) {
for (int y = -center; y <= center; ++y) {
// 卷积权重改变像素
dst.at(i - center, j - center)[0] +=
img.at(i + x, j + y)[0] * gaus[x + center][y + center];
dst.at(i - center, j - center)[1] +=
img.at(i + x, j + y)[1] * gaus[x + center][center];
dst.at(i - center, j - center)[2] +=
img.at(i + x, j + y)[2] * gaus[x + center][center];
}
}
}
}
dst.copyTo(dstImage);
cv::imwrite("../img-1and2/GaussianBlur.jpeg", dstImage);
}