CS224斯坦福nlp课程学习笔记2-词向量
one hot encoder（词袋模型）
每个词表示为一个向量，向量长度为语料库中词的个数，每个向量值只有一个编码为1其余是0
杭州 [0,0,0,0,0,0,0,1,0,……，0,0,0,0,0,0,0]
上海 [0,0,0,0,1,0,0,0,0,……，0,0,0,0,0,0,0]
宁波 [0,0,0,1,0,0,0,0,0,……，0,0,0,0,0,0,0]
北京 [0,0,0,0,0,0,0,0,0,……，1,0,0,0,0,0,0]
缺点：
- 这种方式编码比较随机，向量之间是相互独立的，很难看出向量之间的语义关系。
- 存在数据稀疏问题。向量维度过大，容易造成维度灾难。
word embedding（词向量）
将词转化成一种分布式表示，又称词向量。分布式表示将词表示成一个定长的连续的稠密向量。
- 分布式表示优点:
1、词之间存在相似关系： 是词之间存在“距离”概念，这对很多自然语言处理的任务非常有帮助。
2、包含更多信息： 词向量能够包含更多信息，并且每一维都有特定的含义。在采用one-hot特征时，可以对特征向量进行删减，词向量则不能
- 较著名的采用neural network language
model生成词向量的方法有：Skip-gram、CBOW、LBL、NNLM、C&W、GloVe等。
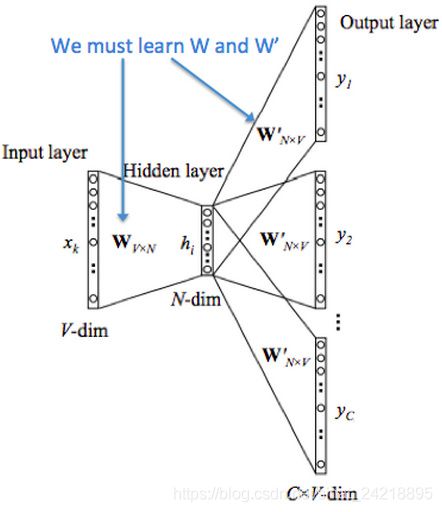
word2vec
通过单词和上下文彼此预测。
- 两个算法：
Skip-grams (SG)：预测上下文
Continuous Bag of Words (CBOW)：预测目标单词 - 两种稍微高效一些的训练方法：
Hierarchical softmax
Negative sampling
其中w(t)代表当前词语位于句子的位置t，同理定义其他记号。在窗口内（上图为窗口大小为5），除了当前词语之外的其他词语共同构成上下文。
skip-gram
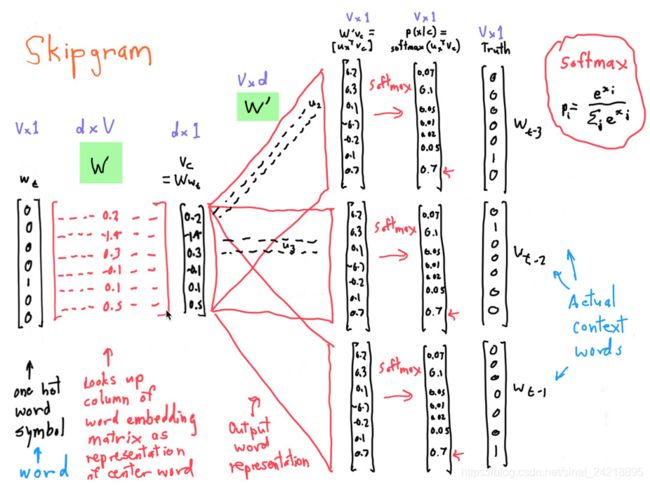
v表示one-hot编码长度，d表示设定的输出向量的维度
1v Vd->1d dv ->1v
最后softmax之前1v向量的多少跟窗口大小有关。if窗口大小n=3最后预测的结果（t-3,t-2,t-1,t+1,t+2,t+3)。
- softmax()结果和truth值比较，前反馈进行参数修正
最后的W和W’都是V*d维的向量（有V个d维的词向量），也就是说同一个词有两个词向量，最终的embedding选择有两种策略：相加、拼接
CBOW
Skip-gram是给定词语预测上下文
cbow是给定上下文预测词语
其他类似于skip-gram
word2vec缺点：
- 每个曾词只有一个向量表示，一词多意的情况没有考虑
- 滑动窗口的局限，只考虑的局部上下文信息，没有考虑全局信息
共现矩阵
例如，有语料如下：
I like deep learning.
I like NLP.
I enjoy flying.
则其共现矩阵如下：
矩阵定义的词向量在一定程度上缓解了one-hot向量相似度为0的问题，但没有解决数据稀疏性和维度灾难的问题。
SVD(奇异值分解)
既然基于co-occurrence矩阵得到的离散词向量存在着高维和稀疏性的问
题，一个自然而然的解决思路是对原始词向量进行降维，从而得到一个稠密的连续词向量。
SVD矩阵分解的方式就能够得到两组向量，分别表示文档的向量（可以用来做文本距离）和单词的向量。
有上面的矩阵进行SVD分解，得到矩阵正交矩阵U，对U进行归一化得到矩阵如下：
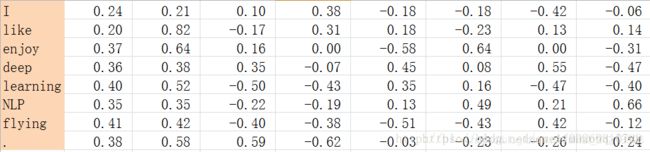
SVD得到了word的稠密（dense）矩阵，该矩阵具有很多良好的性质：语义相近的词在向量空间相近，甚至可以一定程度反映word间的线性关系。
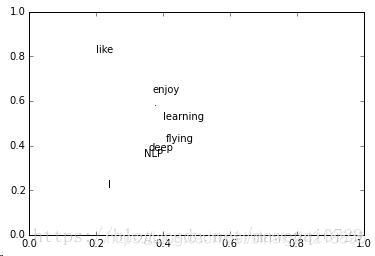
word2vector考虑局部上下文关系
共现矩阵考虑到了全局的信息
结合二者的优点提出了一种glove算法
glove算法`
P(j|i)=Xij/Xi
推导过程参考glove学习笔记``
（ps:自己也有点晕，不想误导大家。。。学会的可以在这个上面补充哦！
学的不好，请大家批评指正）