Transformer中数据维度的变化和mask

会用到的一些函数

nn.Embedding()和padding_idx

a = torch.LongTensor([0,1,2,3,4])
emb = nn.Embedding(10,5,padding_idx=0)
emb(a)

## output:
# tensor([[ 0.0000,  0.0000,  0.0000,  0.0000,  0.0000],
#         [ 1.2378,  0.2666,  0.3143, -0.4785, -0.0261],
#         [ 0.9385,  1.8889, -2.1237,  0.9485, -0.5656],
#         [-0.6171,  0.3276, -0.5347,  0.1167, -0.7167],
#         [-0.5722,  1.7916, -2.8614,  0.1669,  1.2874]],
#        grad_fn=)

在这个句子中，0是所对应的索引，padding_idx=0时，这里不做embedding处理。

unsqueeze(1) 增加维度

a = torch.LongTensor([1,2,3])
print(a.shape)
a = a.unsqueeze(1)
print(a.shape)

# torch.Size([3])
# torch.Size([3, 1])

np.triu创建一个上三角矩阵，右上角为1，左下角为0

print(np.triu(np.ones((1, 8, 8)), k=1).astype('uint8'))
# k=1即从第二列（索引为1）开始；
# [[[0 1 1 1 1 1 1 1]
#   [0 0 1 1 1 1 1 1]
#   [0 0 0 1 1 1 1 1]
#   [0 0 0 0 1 1 1 1]
#   [0 0 0 0 0 1 1 1]
#   [0 0 0 0 0 0 1 1]
#   [0 0 0 0 0 0 0 1]
#   [0 0 0 0 0 0 0 0]]]

在torch.Tensor中查找某个特定值的所有位置

value = 1
print((test_tensor==1).nonzero())

masked_fill用法

a = torch.LongTensor([[1,2,3],[4,5,6]])
masking = torch.LongTensor([[1,1,1],[0,0,0]])
masking = (masking==0) #get the booling value, if equal to 0, then set it to True
a.masked_fill(masking,value=8)
# tensor([[1, 2, 3],
#         [8, 8, 8]])

Layernorm

a = torch.rand((2,50,1,64))
###layernorm的形状即是输入张量的除第一位以外的形状
layer_norm = nn.LayerNorm(a.size()[1:],eps=1e-6)
layer_norm(a)

torch.eq

>>> torch.eq(torch.tensor([[1, 2], [3, 4]]), torch.tensor([[1, 1], [4, 4]]))
tensor([[ True, False],
        [False, True]])

Encoder

Input: batch of sentences with max length = 50

embedding_layer + positional_embedding

[batch_size,max_len,1,embed_size]

在词向量层中，我们需要把对应的index设置为0。在第一次传入Multi-head attention之前，我们可以直接在词向量层中将其设置为0；

Encoder block(xN stacks)

Input size: [batch_size,max_length,1,embed_size]

Multi-head attention

将输入的输入做了上述操作之后，得到Q,K,V三个矩阵，在进行softmax()之前，由于我们不希望看到位置上对应的内容，用masked_fill，将所有原位置的数设置为-inf. 这样softmax()对应的结果就会是0.

接下来详细说明Multi_head中的维度变化：

假设我们一共有num_heads个head, 每个单词对应词向量的大小为embed_size。由于我们希望做了attention之后的输出，维度与输入相同，所以我们把head_size设置为head_size=embed_size\\num_heads，且embed_size % num_heads==0。

因此，$W^Q,W^K,W^V$ 三个矩阵的维度为：

[embed_size, num_heads*head_size]，这里可以理解为把多个头的结果concatenate起来。

将Input分别于这三个矩阵相乘以后，得到的Q,K,V的维度为：

[batch_size,max_length,1,embed_size(num_heads*head_size)]

接下来对Q,K,V进行维度上的变化。

在上面的操作中，Q,K,V可以看做是每个输入经过8个attention head，每个head的size是8，（8*8=64=embed_size）。我们需要将每个head得到的结果分开，然后在每个head中进行softmax的操作。于是有：

K = K.view(batch_size,-1,num_heads,head_size)
##转置
K = K.transpose(1,2)
## K.shape=[batch_size,num_heads,max_length,head_size] 完美！

参考以下这张图：

我们可以理解为，对于同一个句子，我们用num_heads个头去看他，又由于head_size=embed_size\\num_heads，所以会得到这个形状的张量。

softmax()

​ $softmax(\frac{Q\cdot K^T}{\sqrt{di{m}_K}})$

这里还要对K进行一次转置，转置后的结果为：[batch_size, num_heads, head_size, max_length]

Q与K的转置相乘后的结果为：[batch_size, num_heads, max_length, max_length]

这时，我们需要对矩阵进行mask操作；之后我们可以进行softmax。

对$Q\cdot K^T$的结果进行mask

首先，我们可以确定，我们不希望模型看到之后的，这对预测没有帮助，因此在softmax之前可以直接将其设置为-inf，然后softmax得到的结果为0。

对pad进行mask

也存在padding的位置，在进行一个Multi-Head Attention计算后，就使得原来是0的位置不是0，所以attention输出的这些位置也应该为空，所以只需要在attention计算之后把相应的位置替换为0即可

如何对数据进行mask操作

pad mask

test = embed(test_src) # [2, 50, 1, 64]
mask_row = int((test==0).nonzero()[:,0][0]) #mask from this row

# score shape [8,50,50]
mask_1 = torch.ones((8,mask_row+1,50))
mask_2 = torch.zeros((8,MAX_LENGTH-mask_row-1,50))
mask = torch.cat((mask_1,mask_2),dim=1)
mask = (mask==0)

##
a = torch.rand((8,50,50))
a = a.masked_fill(mask,value=0)

Decoder

基本操作与Encoder相同。**不同之处在于，训练时Decoder可以并行；即：在Decoder中输入整个target句子，在做maked self-attention时，我们把将来的信息Mask掉。**得到的矩阵经过self-attention，在这一层注意把mask掉即可；经过linear层后，经过softmax输出一个与target vocabulary大小相同的向量，得到每个单词的概率。

Encoder的output，作为decoder中self-attention的K和V，我们不需要对其进行padding mask，我们只对Q进行padding mask，Q是target转化而来的。

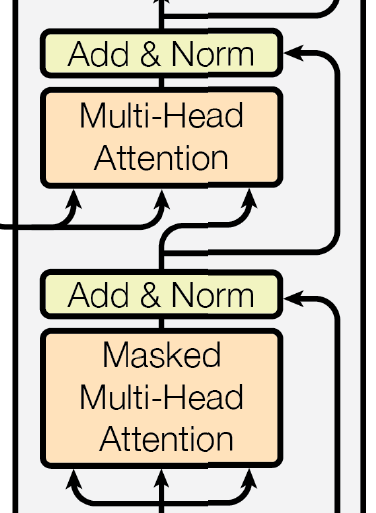
Decoder中Masked Multi-Head Attention中的Mask(第一个attention)

其次我们需要注意的是，在decoder训练过程中，输入可以是一个完整的句子，我们设置一个上三角矩阵mask，即：第一行只看到一个单词，第二行看到两个，第三行看到三个…以此类推，直到最后一行才能看到整个完整的句子。

例如我们得到如下的一个masked multi-head attention的输出：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-vI8wnxOg-1610524746734)(https://i.loli.net/2021/01/08/VtTsuoLkKNdOw8C.png)]

第一行是我们用来预测第二个单词；然后，用第二行预测第三个单词；用第三行预测第四个单词…

Multihead attention中的mask(第二个attention)

跟Encoder中的类似，对$softmax(\frac{Q\cdot K^T}{\sqrt{di{m}_K}})V$中的$Q\cdot K^T$后，对Q中原本的进行mask。softmax之后，再次对进行mask。

Tips:

总的来看，transformer训练的时候是用ground truth来进行teacher forcing，预测的时候需要一个单词一个单词的预测。