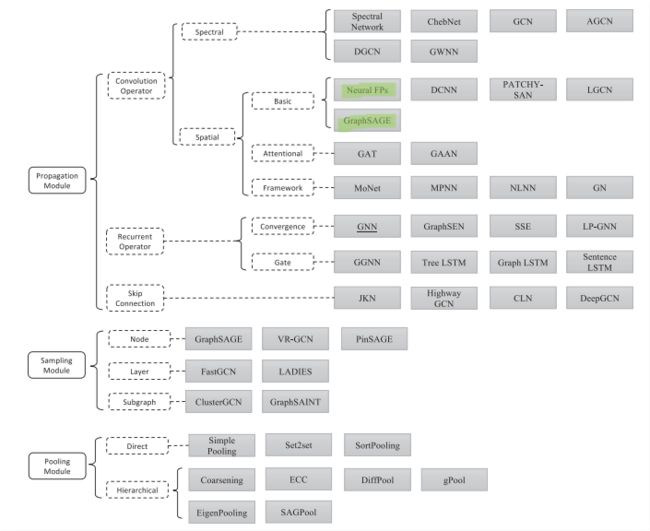
图神经网络12-分子指纹GCN:Neural FPs
1 Neural FPs论文简介
论文:Convolutional Networks on Graphs for Learning Molecular Fingerprints 图卷积网络用于学习分子指纹
链接:http://arxiv.org/pdf/1509.09292.pdf
作者:David Duvenaud†, Dougal Maclaurin†, Jorge Aguilera-Iparraguirre (哈佛大学)
来源:NIPS 2015
代码:https://github.com/HIPS/neural-fingerprint
本文引入了直接在图上运行的卷积神经网络,这些网络允许端到端学习和预测,输入是任意大小和形状的Graph。 我们介绍的架构可以作为基于圆形指纹的标准分子特征提取方法,通过实验表明这些基于Graph数据提取的特征更具解释性,并且在各种任务上具有更好的预测性能。
2 论文动机
最新材料设计方面的工作使用神经网络在数据样本中归纳总结,然后来预测新型分子的属性或者性质。这类任务的一个难点是,对预测变量的输入
分子的大小和形状是任意的,没有固定的。当前,大多数机器学习框架只能
处理固定大小的输入,一般情况是使用现成的指纹软件,计算固定尺寸的特征向量,并将这些特征用作全连接的输入深度神经网络或其他传统的机器学习方法。在训练期间,将分子指纹载体视为固定的不变的。
在本文中,我们用一个输入为原始分子图的可微神经网络代替了该堆栈的底层——计算分子指纹向量的函数。在这个图中,顶点代表单个原子,边代表键。这个网络的底层是卷积的,因为相同的局部过滤器被应用到每个原子和它的邻居。经过几个这样的层之后,一个全局池步骤结合了分子中所有原子的特征。
这些神经图指纹比固定指纹有几个优点:
-
预测能力强:通过实验比较可以发现,我们的模型比传统的指纹向量能够提供更好的预测能力。
-
模型简洁:为了对所有可能的子结构进行编码,传统的指纹向量必须维度非常高。而我们的模型只需要对相关特征进行编码,模型的维度相对而言低得多,这降低了下游的计算量。
-
可解释性:传统的指纹向量对每个片段fragment 进行不同的编码,片段之间没有相似的概念。即:相似的片段不一定有相似的编码;相似的编码也不一定代表了相似的片段。
论文的模型中,每个特征都可以由相似但是不同的分子片段激活,因此相似的片段具有相似的特征,相似的特征也代表了相似的片段。这使得特征的representation 更具有意义。
3 分子指纹(Molecular Fingerprint)
在比较两个化合物之间的相似性时遇到的最重要问题之一是任务的复杂性,这取决于分子表征的复杂性。 为了使分子的比较在计算上更容易,需要一定程度的简化或抽象。分子指纹就是一种分子的抽象表征,它将分子转化(编码)为一系列比特串(即比特向量,bit vector .),然后可以很容易地在分子之间进行比较。典型的流程是将提取分子的结构特征、然后哈希(Hashing)生成比特向量。
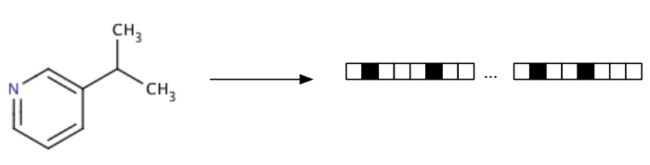
比较分子是很难的,比较比特串却很容易,分子之间的比较必须以可量化的方式进行。分子指纹上的每个比特位对应于一种分子片段(Figure 2),假设相似的分子之间必然有许多公共的片段,那么具有相似指纹的分子具有很大的概率在2D结构上也是相似的。
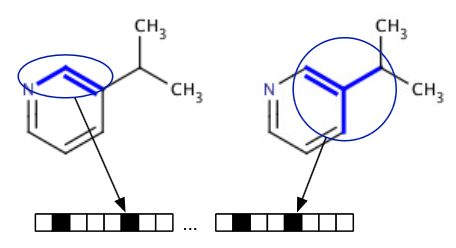
有十多种方法可以评估两个向量之间的相似性(参见:Fingerprints-Screening and Similarity.),最常见的是欧几里德距离。但对于分子指纹,行业标准是Tanimoto系数,它由两个指纹中设置为1的公共位数除以两个指纹之间设置为1的总位数组成。这意味着Tanimoto系数总是具有介于1和0之间的值,而不管指纹的长度如何,这导致指纹随着指纹变长而变得松散。这种损失还意味着具有给定Tanimoto系数的两个指纹实际上将如何相似地将极大地取决于所使用的指纹的类型,这使得不可能选择用于确定两个指纹是相似还是不相似的通用截止标准。然而,通过数据融合策略将分子指纹与其他相似系数相结合,可以提高分子指纹的性能[1]。表1列出了几个与指纹一起使用的相似性和距离度量。

其中,给定两个化合物A和B的指纹,m等于指纹中存在的总位数,a、b分别等于A、B中比特值为1的位数,c等于A和B中公共的比特值为1的位数。
4 圆形指纹算法
分子指纹的最新技术是扩展连接性圆形指纹 extended-connectivity circular fingerprints:ECFP 。ECFP 是对Morgan 算法的改进,旨在以无关于原子标记顺序atom-relabling的方式来识别分子中存在哪些亚结构。
ECFP 通过对前一层邻域的特征进行拼接,然后采用一个固定的哈希函数来抽取当前层的特征。哈希函数的结果视为整数索引,然后对顶点 feature vector 在索引对应位置处填写 1 。
不考虑hash 冲突,则指纹向量的每个索引都代表一个特定的亚结构。索引表示的亚结构的范围取决于网络深度,因此网络的层数也被称为指纹的“半径”。
ECFP 类似于卷积网络,因为它们都在局部采用了相同的操作,并且在全局池化中聚合信息。
ECFP 的计算框架如下图所示:
首先通过分子结构构建分子图,其中顶点表示原子、边表示化学键。在每一层,信息在邻域之间流动。图的每个顶点在一个固定的指纹向量中占据一个bit。其中这只是一个简单的示意图,实际上每一层都可以写入指纹向量。
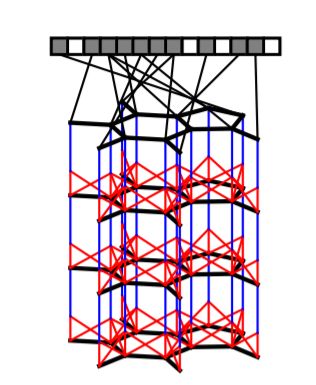
圆形指纹算法:
(1) 输入:
- 分子结构
- 半径参数 R R R
- 指纹向量长度 S S S
(2) 输出:
- 指纹向量 f f f
(3) 算法步骤:
- 初始化指纹向量: f ⟵ 0 s f \longleftarrow 0_{s} f⟵0s
- 遍历每个原子 a a a,获取每个原子的特征: r a ⟵ g ( a ) r_{a} \longleftarrow g(a) ra⟵g(a)
- 遍历每一层。对于第 L L L层,迭代步骤为:
遍历分子中的每个原子 a a a,对于每个原子 a a a计算:
<1>获取顶点 a a a的领域原子的特征: r 1 , . . . , r N = n e i g h b o r s ( a ) r_{1},...,r_{N}=neighbors(a) r1,...,rN=neighbors(a)
<2>拼接顶点 a a a及其领域原子特征:
v ⟵ [ r a , r 1 , . . . , r N ] v \longleftarrow [r_{a},r_{1},...,r_{N}] v⟵[ra,r1,...,rN]
<3>执行哈希函数得到顶点 a a a的当前特征:
r a ⟵ h a s h ( v ) r_{a} \longleftarrow hash(v) ra⟵hash(v)
<4>执行索引函数: i ⟵ m o d ( r a , S ) i\longleftarrow mod(r_{a},S) i⟵mod(ra,S)
<5>登记索引: f i ⟵ 1 f_{i} \longleftarrow1 fi⟵1
(4)最后返回分子指纹向量(0-1): f f f
5 分子指纹GCN算法
分子指纹GCN算法选择类似于现有ECFP 的神经网络架构:
哈希操作Hashing:在ECFP 算法中,每一层采用哈希操作的目的是为了组合关于每个原子及其邻域子结构的信息。
本文利用一层神经网络代替哈希运算。当分子的局部结构发生微小的变化时(神经网络是可微的,因此也是平滑的),这种平滑函数可以得到相似的激活值。
索引操作Indexing:在 ECFP 算法中,每一层采用索引操作的目的是将每个原子的特征向量组合成整个分子指纹。每个原子在其特征向量的哈希值确定的索引处,将指纹向量的单个比特位设置为1,每个原子对应一个1 。这种操作类似于池化,它可以将任意大小的Graph 转换为固定大小的向量。
这种索引操作的一个缺点是:当分子图比较小而指纹长度很大时,最终得到的指纹向量非常稀疏。然后论文使用softmax 操作视作索引操作的一个可导的近似。本质上这是要求将每个原子划分到一组类别的某个类别中。所有原子的这些类别向量的总和得到最终的指纹向量。其操作也类似于卷积神经网络中的池化操作。
规范化Canonicalization:无论原子的邻域原子的顺序如何变化,圆形指纹是不变的。实现这种不变性的一种方式是:在算法过程中,根据相邻原子的特征和键特征对相邻原子进行排序。论文里尝试了这种排序方案,还对局部邻域的所有可能排列应用了局部特征变换。另外,一种替代方案是应用排序不变函数permutation-invariant, 如求和。为了简单和可扩展性,论文里选择直接求和。
GCN网络指纹算法:
(1) 输入:
- 分子结构molecule
- 半径参数 R R R
- 隐藏参数: H 1 1 . . . H R 5 H_{1}^{1}...H_{R}^{5} H11...HR5
- 输出层参数: W 1 . . . W R W_{1}...W_{R} W1...WR
对不同的键数量,采用不同的隐层参数 H H H(最多五个键)
(2) 输出:(实数)指纹向量
(3) 算法步骤:
- 初始化指纹向量: f ⟵ 0 s f \longleftarrow 0_{s} f⟵0s
- 遍历每个原子 a a a,获取每个原子的特征: r a ⟵ g ( a ) r_{a} \longleftarrow g(a) ra⟵g(a)
- 遍历每一层。对于第 L L L层,迭代步骤为:
遍历分子中的每个原子 a a a,对于每个原子 a a a计算:
<1>获取顶点 a a a的领域原子的特征: r 1 , . . . , r N = n e i g h b o r s ( a ) r_{1},...,r_{N}=neighbors(a) r1,...,rN=neighbors(a)
<2>池化顶点 a a a及其领域 r i r_{i} ri的原子的特征: v ⟵ r a + ∑ i = 1 N r i v \longleftarrow r_{a}+\sum_{i=1}^{N} r_{i} v⟵ra+∑i=1Nri
<3>执行哈希函数 i ⟵ s o f t m a x ( r a W L ) i \longleftarrow softmax(r_{a}W_{L}) i⟵softmax(raWL)
<4> 登记索引: f ⟵ f + i f \longleftarrow f+i f⟵f+i
(4) 返回向量 f f f
ECFP 圆形指纹可以解释为具有较大随机权重的神经网络指纹算法的特殊情况。在较大的输入权重情况下, t a n h tanh tanh激活函数接近阶跃函数。而级联的阶跃函数类似于哈希函数。
在较大的输入权重情况下,softmax 函数接近一个one-hot 的 argmax 操作,这类似于索引操作。
6 实验部分
6.1 随机权重
分子指纹的一个用途是计算分子之间的距离。这里我们检查基于 ECFP 的分子距离是否类似于基于随机的神经网络指纹的分子距离。
我们选择指纹向量的长度为 2048,并使用Jaccard 相似度来计算两个分子的指纹向量之间的距离:
![]()
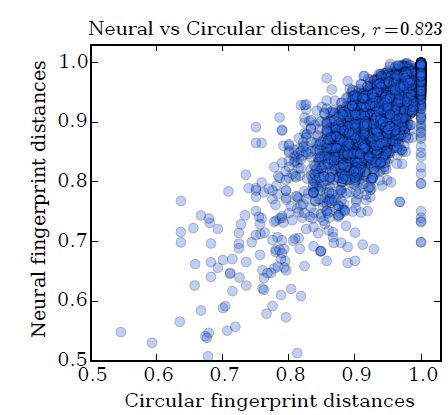
我们的数据集为溶解度数据集,下图为使用圆形指纹和神经网络指纹的成对距离散点图,其相关系数为: r = 0.823 r=0.823 r=0.823
图中每个点代表:相同的一对分子,采用圆形指纹计算到的分子距离、采用神经网络指纹计算得到的分子距离,其中神经网络指纹模型采用大的随机权重。
距离为1.0 代表两个分子的圆形指纹没有任何重叠;距离为0.0 代表两个分子的圆形指纹完全重叠。
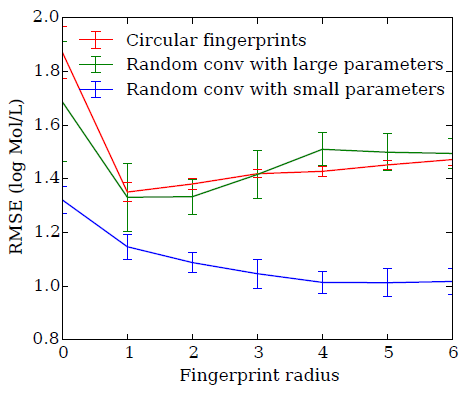
我们将圆形指纹、随机神经网络指纹接入一个线性回归层,从而比较二者的预测性能。
圆形指纹、大的随机权重的随机神经网络指纹,二者的曲线都有类似的轨迹。这表明:通过大的随机权重初始化的随机神经网络指纹和圆形指纹类似。
较小随机权重初始化的随机神经网络指纹,其曲线与前两者不同,并且性能更好。
即使是未经训练的神经网络,神经网络激活值的平滑性也能够有助于模型的泛化。
6.2 可解释性
圆形指纹向量的特征(即某一组bit 的组合)只能够通过单层的单个片段激活(偶然发生的哈希碰撞除外),神经网络指纹向量的特征可以通过相同结构的不同变种来激活,从而更加简洁和可解释。
为证明神经网络指纹是可接受的,我们展示了激活指纹向量中每个特征对应的亚结构类别。
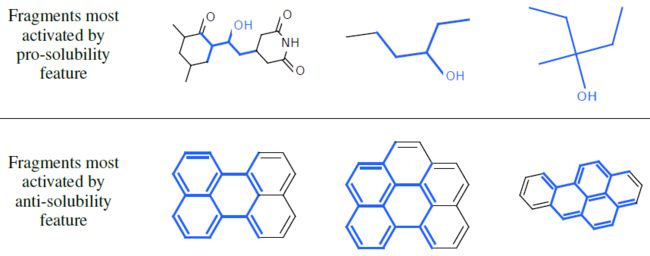
溶解性特征:我们将神经网络指纹模型作为预训溶解度的线性模型的输入来一起训练。下图展示了对应的片段(蓝色),这些片段可以最大程度的激活神经网络指纹向量中最有预测能力的特征。
上半图:激活的指纹向量的特征与溶解性具有正向的预测关系,这些特征大多数被包含亲水性R-OH 基团(溶解度的标准指标)的片段激活。
下半图:激活的指纹向量的特征与溶解性具有负向的预测关系(即:不溶解性),这些特征大多数被非极性的重复环结构激活。
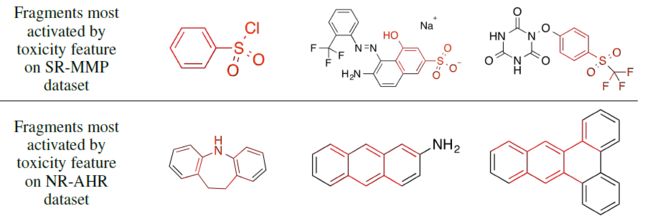
毒性特征:我们用相同的架构来预测分子毒性。下图展示了对应的片段(红色),这些片段可以最大程度的激活神经网络指纹向量中最有预测能力的特征。
上半图:激活的指纹向量的特征与毒性具有正向的预测关系,这些特征大多数被包含芳环相连的硫原子基团的片段激活。
下半图:激活的指纹向量的特征与毒性具有正向的预测关系,这些特征大多数被稠合的芳环(也被称作多环芳烃,一种著名的致癌物)激活。
6.3 模型比较
数据集:论文在多个数据集上比较圆形指纹和神经网络指纹的性能:
- 溶解度数据集:包含 1144 个分子,及其溶解度标记。
- 药物功效数据集:包含 10000 个分子,及其对恶行疟原虫(一种引发疟疾的寄生虫)的功效。
- 有机光伏效率数据集:哈佛清洁能源项目使用昂贵的 DFT 模拟来估算有机分子的光伏效率,我们从该数据集中使用 20000 个分子作为数据集。
论文中的 pipeline 将每个分子编码的 SMILES 字符串作为输入,然后使用 RDKit 将其转换为Graph 。我们也使用 RDKit 生成的扩展圆形指纹作为 baseline 。这个过程中,氢原子被隐式处理。
ECFP 和神经网络中用到的特征包括:
- 原子特征:原子元素类型的 one-hot、原子的度degree、连接氢原子的数量、隐含价implicit valence、极性指示aromaticity indicator。
- 键特征:是否单键、是否双键、是否三键、是否芳族键、键是否共轭、键是否为环的一部分。
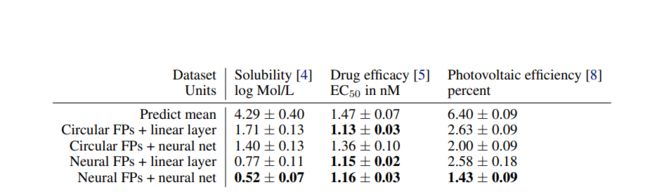
结果如下图所示。可以看到在所有实验中,神经网络指纹均达到或者超过圆形指纹的性能,并且使用神经网络层的方式(neural net )超过了线性层的方式(linear layer)。
7 核心代码
import autograd.numpy as np
from util import memoize, WeightsParser
from rdkit_utils import smiles_to_fps
def batch_normalize(activations):
mbmean = np.mean(activations, axis=0, keepdims=True)
return (activations - mbmean) / (np.std(activations, axis=0, keepdims=True) + 1)
def relu(X):
"Rectified linear activation function."
return X * (X > 0)
def sigmoid(x):
return 0.5*(np.tanh(x) + 1)
def mean_squared_error(predictions, targets):
return np.mean((predictions - targets)**2, axis=0)
def categorical_nll(predictions, targets):
return -np.mean(predictions * targets)
def binary_classification_nll(predictions, targets):
"""Predictions is a real number, whose sigmoid is the probability that
the target is 1."""
pred_probs = sigmoid(predictions)
label_probabilities = pred_probs * targets + (1 - pred_probs) * (1 - targets)
return -np.mean(np.log(label_probabilities))
def build_standard_net(layer_sizes, normalize, L2_reg, L1_reg=0.0, activation_function=relu,
nll_func=mean_squared_error):
"""Just a plain old neural net, nothing to do with molecules.
layer sizes includes the input size."""
layer_sizes = layer_sizes + [1]
parser = WeightsParser()
for i, shape in enumerate(zip(layer_sizes[:-1], layer_sizes[1:])):
parser.add_weights(('weights', i), shape)
parser.add_weights(('biases', i), (1, shape[1]))
def predictions(W_vect, X):
cur_units = X
for layer in range(len(layer_sizes) - 1):
cur_W = parser.get(W_vect, ('weights', layer))
cur_B = parser.get(W_vect, ('biases', layer))
cur_units = np.dot(cur_units, cur_W) + cur_B
if layer < len(layer_sizes) - 2:
if normalize:
cur_units = batch_normalize(cur_units)
cur_units = activation_function(cur_units)
return cur_units[:, 0]
def loss(w, X, targets):
assert len(w) > 0
log_prior = -L2_reg * np.dot(w, w) / len(w) - L1_reg * np.mean(np.abs(w))
preds = predictions(w, X)
return nll_func(preds, targets) - log_prior
return loss, predictions, parser
def build_fingerprint_deep_net(net_params, fingerprint_func, fp_parser, fp_l2_penalty):
"""Composes a fingerprint function with signature (smiles, weights, params)
with a fully-connected neural network."""
net_loss_fun, net_pred_fun, net_parser = build_standard_net(**net_params)
combined_parser = WeightsParser()
combined_parser.add_weights('fingerprint weights', (len(fp_parser),))
combined_parser.add_weights('net weights', (len(net_parser),))
def unpack_weights(weights):
fingerprint_weights = combined_parser.get(weights, 'fingerprint weights')
net_weights = combined_parser.get(weights, 'net weights')
return fingerprint_weights, net_weights
def loss_fun(weights, smiles, targets):
fingerprint_weights, net_weights = unpack_weights(weights)
fingerprints = fingerprint_func(fingerprint_weights, smiles)
net_loss = net_loss_fun(net_weights, fingerprints, targets)
if len(fingerprint_weights) > 0 and fp_l2_penalty > 0:
return net_loss + fp_l2_penalty * np.mean(fingerprint_weights**2)
else:
return net_loss
def pred_fun(weights, smiles):
fingerprint_weights, net_weights = unpack_weights(weights)
fingerprints = fingerprint_func(fingerprint_weights, smiles)
return net_pred_fun(net_weights, fingerprints)
return loss_fun, pred_fun, combined_parser
def build_morgan_fingerprint_fun(fp_length=512, fp_radius=4):
def fingerprints_from_smiles(weights, smiles):
# Morgan fingerprints don't use weights.
return fingerprints_from_smiles_tuple(tuple(smiles))
@memoize # This wrapper function exists because tuples can be hashed, but arrays can't.
def fingerprints_from_smiles_tuple(smiles_tuple):
return smiles_to_fps(smiles_tuple, fp_length, fp_radius)
return fingerprints_from_smiles
def build_morgan_deep_net(fp_length, fp_depth, net_params):
empty_parser = WeightsParser()
morgan_fp_func = build_morgan_fingerprint_fun(fp_length, fp_depth)
return build_fingerprint_deep_net(net_params, morgan_fp_func, empty_parser, 0)
def build_mean_predictor(loss_func):
parser = WeightsParser()
parser.add_weights('mean', (1,))
def loss_fun(weights, smiles, targets):
mean = parser.get(weights, 'mean')
return loss_func(np.full(targets.shape, mean), targets)
def pred_fun(weights, smiles):
mean = parser.get(weights, 'mean')
return np.full((len(smiles),), mean)
return loss_fun, pred_fun, parser
8 参考资料
- 五、分子指纹GCN
- 分子指纹及其在虚拟筛选中的应用