【机器学习十八番武艺】朴素贝叶斯分类器

朴素贝叶斯分类器

贝叶斯分类器是一类分类算法的总称，这类算法均以贝叶斯定理作为基础。

数学原理

贝叶斯方法最早由英国牧师托马斯·贝叶斯在《论有关机遇问题的求解》中提出一种归纳推理的理论，当时并没有被数学界普遍接受。到了20世纪中叶，在传统统计学出现困难的时候，贝叶斯方法被重新提出，并发展成为一种新的统计学。有别于传统统计学，贝叶斯统计学引入了先验概率分布这一概念，在统计学模型中更加注重人的主观判断。例如，对于一个每天都要品茶的女士来说，他能分辨出茶中是先加的牛奶还是先加的茶叶的概率要比不喝茶的人要高得多。在统计模型中加入先验概率分布，在处理小样本数据时往往会有更好的表现。
贝叶斯分类器在数学上主要是基于贝叶斯公式。贝叶斯公式的推导过程：
联合概率:

于是就有：

将贝叶斯公式用于分类问题，我们有

我们最终是想求得基于给定的特征下，目标数据属于某一类别的概率p(类别|特征)。然后，我们比较他属于各类别概率的大小，认为他应归类到概率最大的类别。可以看出，贝叶斯分类器的本质就是最大后验概率估计。
在实际计算中，因为所有的p(特征)都是一样的，所以在实际计算中我们只需要计算联合概率暨p(特征|类别)p(类别)的大小。
以上是基于一个特征进行分类的原理，同样的在基于多个特征进行分类的时候我们有

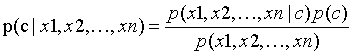
其中，c表示类别，x1、x2、…、xn表示样本提供的n个特征。
由于上式子中分母的都一样，只需要比较分子的大小。但实际上p（x1,x2,…，xn）仍旧比较难直接求出。于是在朴素贝叶斯中引入了一个很强的假设，假设所有的特征x1、x2、…、xn相互独立。于是我们有

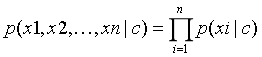
朴素贝叶斯分类器适用于有监督学习的分类问题。优点是简单易懂、学习效率高，在某些领域分类问题中能出现很好的结果。缺点是自变量之间的独立性假设在现实中很难满足；连续变量的正态性假设也会对结果的精度产生影响。

python实现

介绍完上面的数学理论，下面我们用python动手写一个朴素贝叶斯分类器。

#-*- coding:utf-8 -*-
import numpy as np

def NaiveBayes(traindata, trainlabel):
	classes = 10 #类别数
	features = 784 #样本维度

	sampleNum = trainlabel.shape[0]
	
	#计算p（c）
	Pc = np.zeros((classes, 1))
	for c in range(classes):
		c_i = (trainlabel == c) #统计标签中类别c的样本数量
		c_i_num = np.sum(c_i)
		Pc[c] = (c_i_num+1)/sampleNum #laplace校准
	Pc = np.log(Pc)
	
	#计算p(x|c)
	y_num = 2 #每个特征可能的取值个数
	c_f_y_count = np.zeros((classes, feature, y_num)) #统计每个类别每个特征的每种可能出现次数
	for k in range(sampleNum):
		c = trainlabel[k]
		data = traindata[k]
		for f in range(featrues):
			y = data[f]
			c_f_y_count[c][f][y] += 1
	
	Px_c = np.zeros((classes, featrues, y_num)) #统计每个类别每个特征的每种可能取值的概率
	for c in range(classes):
		for f in range(features):
			c_f_y_num = np.sum(c_f_y_count[c][f])
			for y in range(y_num):
				Px_c[c][f][y] = np.log((c_f_y_count[c][f][y]+1)/c_f_y_num)
	return Pc, Px_c
	
def predict(Pc, Px_c, x):
	classes = 10
	features = 784
	Pc_x = [0]*classes #记录每个类别的后验概率
	for c in range(classes):
		Px_c_sum = 0
		for f in range(features):
			Px_c_sum += Px_c[c][f][x[f]] #对概率值取log 连乘变成了求和运算
		Pc_x[c] = Px_c_sum + Pc[c]
	pre_c = Pc_x.index(max(Pc_x)) #找到每个类别的后验概率中的最大值对应的类别
	return pre_c

def test(Pc, Px_c, testdata, testlabel):
	sampleNum = testlabel.shape[0]
	count = 0.0
	for i in range(sampleNum):
		data = testdata[i]
		label = testlabel[i]
		pre_label = predict(Pc, Px_c, data)
		if(pre_label == label):
			count += 1
	acc = count/sampleNum
	return acc

if __name__ == '__main__':
	traindata,trainlabel = loadData('../Mnist/mnist_train.csv')
	evaldata,evallabel = loadData('../Mnist/mnist_test.csv')

	Pc,Px_c = NaiveBayes(traindata,trainlabel)
	accuracy = test(Pc, Px_c, evaldata, evallabel)
	print('accuracy rate is:',accuracy)

实例（基于scikit-learn）

kaggle上的泰坦尼克幸存者预测

kaggle.com目前将泰坦尼克号ML竞赛作为熟悉 Kaggle 平台工作原理的最佳挑戰。此项比赛会不停地重开，以便带领新人熟悉kaggle平台，同时泰坦尼克号幸存者预测也一个经典的机器学习分类的应用场景。

竞赛的目的很简单：使用机器学习创建一个模型，预测哪些乘客在泰坦尼克号沉船事件中能幸存下来。数据集的下载地址：
https://www.kaggle.com/c/titanic/data

使用贝叶斯分类器预测代码如下：

# -*- coding:utf-8 -*-
import numpy as np
import pandas as pd
import matplotlib.pylab as plt
from sklearn.preprocessing import StandardScaler
from sklearn.naive_bayes import BernoulliNB #伯努利模型

#读入数据
datatrain = pd.read_csv('train.csv')
datatest = pd.read_csv('test.csv')

#去掉几种无用特征
datatrain = datatrain.drop(labels=['PassengerId', 'Name', 'Ticket', 'Cabin'], axis=1)
datatest = datatest.drop(labels=['PassengerId', 'Name', 'Ticket', 'Cabin'], axis=1)

#去除缺失值
datatrain = datatrain.dropna()
#填补测试集的缺失值
datatest = datatest.fillna(datatest.mean()['Age':'Fare'])

#属性转化为数值型
datatrain_dummy = pd.get_dummies(datatrain[['Sex', 'Embarked']])
datatest_dummy = pd.get_dummies(datatest[['Sex', 'Embarked']])

#编码后和数据拼接
datatrain_conti = pd.DataFrame(datatrain, columns=['Survived', 'Pclass', 'Age', 'SibSp', 'Parch','Fare'], index=datatrain.index)
datatrain = datatrain_conti.join(datatrain_dummy)
datatest_conti = pd.DataFrame(datatrain, columns=['Survived', 'Pclass', 'Age', 'SibSp', 'Parch','Fare'], index=datatest.index)
datatest = datatest_conti.join(datatest_dummy)

X_train = datatrain.iloc[:,1:]
y_train = datatrain.iloc[:,0]
X_test = datatest

#标准化
stdsc = StandardScaler()
X_train_conti_std = stdsc.fit_transform(X_train[['Age''SibSp','Parch','Fare']])
X_test_conti_std = stdsc.fit_transform(X_test[['Age''SibSp','Parch','Fare']])

#将ndarray转为datatrainframe
X_train_conti_std = pd.DataFrame(data=X_train_conti_std,columns=['Age''SibSp','Parch','Fare'],index=X_train.index)
X_test_conti_std = pd.DataFrame(data=X_test_conti_std,columns=['Age''SibSp','Parch','Fare'],index=X_test.index)

#有序分类变量Pclass
X_train_cat = X_train[['Pclass']]
X_test_cat = X_test[['Pclass']]

#无序已编码的分类变量
X_train_dummy = X_train[['Sex_female','Sex_male','Embarked_Q','Embarked_S']]
X_test_dummy = X_test[['Sex_female','Sex_male','Embarked_Q','Embarked_S']]

#拼接为datatrainframe
X_train_set = [X_train_cat, X_train_conti_std, X_train_dummy]
X_test_set = [X_test_cat, X_test_conti_std, X_test_dummy]
X_train = pd.concat(X_train_set, axis=1)
X_test = pd.concat(X_test_set, axis=1)

clf = BernoulliNB()
clf.fit(X_train,y_train)
predicted = clf.predict(X_test)
datatest['Survived'] = predicted.astype(int)
datatest[['PassengerId','Survived']].to_csv('submission.csv', sep=',', index=False)

新闻主题分类

文本分类指的是这样一类分类任务。在使用数据挖掘分类方法的基础上，经过训练标记示例模型，对文本片段、段落或文件进行分组和归类。
本次实验我们使用sklearn中的fetch_20newsgroups。
20 newsgroups数据集18000多篇新闻文章，一共涉及到20种话题，分为训练集和测试集，通常用来做文本分类，均匀分为20个不同主题的新闻组集合。fetch_20newsgroups数据集是被用于文本分类、文本挖据和信息检索研究的国际标准数据集之一。
代码如下：

# -*- coding:utf-8 -*-
from sklearn.datasets import fetch_20newsgroups
from sklearn.cross_validation import train_test_split
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.naive_bayes import MultinomialNB

#从互联网下载数据
news = fetch_20newsgroups(subset='all') 
#随机抽取25%的数据样本作为测试集
X_train, X_test, y_train, y_test = train_test_split(news.data, news.target, test_size=0.25, random_state=33) 
#文本特征向量转换
vec = CountVectorizer()
X_train = vec.fit_transform(X_train)
X_test = vec.fit_transform(X_test)
#建立贝叶斯分类器
mnb = MultinomialNB()
mnb.fit(X_train, y_train)
y_predict = mnb.predict(X_test)