poj1182食物链（种类并查集）

http://poj.org/problem?id=1182

r[x] = 0 表示x和父亲是同类
r[x] = 1 表示x吃父亲
r[x] = 2 表示x被父亲吃
因为只存在三种动物，且三种动物构成了环形
所以动物之间的关系是可推导的。

如图：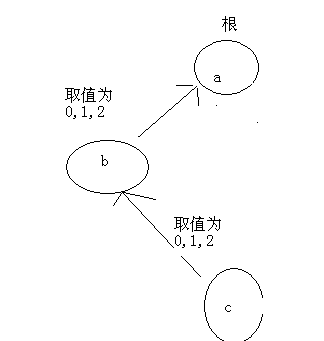

c与a的关系为(r[b] + r[c])%3; b与父亲a的关系可为0,1,2      c与父亲b的关系为0,1,2 。每种取值时，自己在纸上推导一下，就能得到这个关系。

路径压缩的时候就要用到这个关系来修改r[c]， 

如何判断 D a b 是不是假话呢？   当fa == fb 时。说明动物a和b都在一个集合里。那么可以推导它们之间的关系

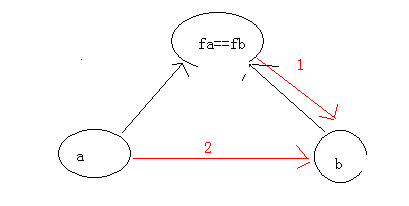
我们已知两条黑线，我们要求得是红线2，即a与b的关系。  如果知道红线1，那么推导a和b的关系，那么就和上面那个图一样

红线1 = (3 - r[b])%3;  这个枚举一下r[b]的取值，然后推一下就知道了

所以如果  (r[a] + 3-r[b])%3==d-1  那么就是真话

如果fa!=fb。 那么就要合并两个集合

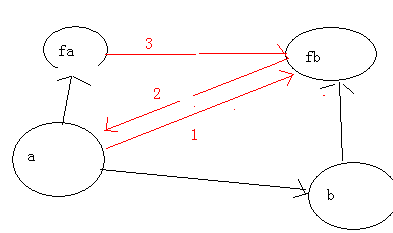。道理和上面一样，先求红线1，然后求红线2，继而求出红线3.然后合并两个集合

 

 1 #include <stdio.h>

 2 int father[55555],r[55555];

 3 

 4 void init(int n)

 5 {

 6     for(int i=1; i<=n; ++i)

 7     {

 8         father[i] = i;

 9         r[i] = 0;

10     }

11 }

12 

13 int find(int x)

14 {

15     if(x==father[x]) return father[x];

16     int t = find(father[x]);

17     r[x] = (r[father[x]] + r[x])%3;

18     father[x] = t;

19     return father[x];

20     /*

21     路径压缩时关系的推导，r[father[x]] 是father[x]和根结点的关系，r[x]是x和father[x]的关系

22     */

23 }

24 int main()

25 {

26     int n,k,i,d,x,y,ans,fx,fy;

27     scanf("%d%d",&n,&k);

28     {

29         ans = 0;

30         init(n);

31         for(i=0; i<k; ++i)

32         {

33             scanf("%d%d%d",&d,&x,&y);

34             if(x>n || y>n ||(d==2 && x==y)) ans++;

35             else

36             {

37                 fx = find(x);

38                 fy = find(y);

39                 if(fx==fy)

40                 {

41                     if((r[x]+3-r[y])%3!=d-1) ans++;

42                 }

43                 else

44                 {

45                     father[fx] = fy;

46                     //r[fy] = (r[x]-r[y]+d-1+3)%3;

47                         r[fx] =  (d-1+r[y]-r[x])%3;

48                 }

49             }

50         }

51         printf("%d\n",ans);

52     }

53     return 0;

54 }