智能优化算法:人工蜂鸟算法 - 附代码
智能优化算法:人工蜂鸟算法
摘要:人工蜂鸟算法( AHA )是 ZHAO 等 于 2021 年提出的一种新型元启发式优化算法 . 该算法模拟了自然界中蜂鸟轴向飞行、对角飞行、全方位飞行 3 种特殊飞行技能和引导觅食、区域觅食、迁移觅食 3 种智能觅食策略,并通过引入访问表来实现蜂鸟寻找和选择食物来源的记忆功能,最终达到求解最优化问题的目的 .
1.人工蜂鸟算法
1.1 初始化
AHA 将 n n n 只蜂鸟放置在 n n n 种食物源上, 随机初 始化食物源位置:
x i = S L + r ⋅ ( S u − S L ) , i = 1 , 2 , ⋯ , n (1) x_i=S_{\mathrm{L}}+r \cdot\left(S_{\mathrm{u}}-S_{\mathrm{L}}\right), i=1,2, \cdots, n \tag{1} xi=SL+r⋅(Su−SL),i=1,2,⋯,n(1)
式中: x i x_i xi 表示第 i i i 个食物源位置; n n n 表示种群规模; S u 、 S L S_u 、 S_{\mathrm{L}} Su、SL 分别表示搜索空间上、下限值; r r r 表示 [ 0 , 1 ] [0,1] [0,1] 之 间均匀分布的随机数.
食物来源访问表初始化如下:
V i , j = { 0 , if i ≠ j null, i = j , i = 1 , 2 , ⋯ , n ; j = 1 , 2 , ⋯ , n (2) V_{i, j}=\left\{\begin{array}{cc} 0, & \text { if } i \neq j \\ \text { null, } & i=j \end{array}, i=1,2, \cdots, n ; j=1,2, \cdots, n\right. \tag{2} Vi,j={0, null, if i=ji=j,i=1,2,⋯,n;j=1,2,⋯,n(2)
式中: i = j i=j i=j 表示蜂鸟在特定的食物来源处受食; i ≠ j i \neq j i=j 表示当前迭代中第 j j j 个食物源被第 i i i 只蜂鸟访问过.
1.2 引导觅食
AHA 中, 蜂鸟为了获得更多的花蜜, 会在相同 访问级别的食物源中访问花蜜补充率最高的食物源. 在受食过程中, 通过引人方向切换向量描述全向飞 行、对角飞行和轴向飞行 3 种技能, 用于控制 d d d 维空 间中的一个或多个方向是否可行. 轴向飞行、对角飞 行、全向飞行技能分别描述如下:
D ( i ) = { 1 , if i = rand ( [ 1 , d ] ) 0 , else (3) \begin{gathered} D^{(i)}= \begin{cases}1, & \text { if } i=\operatorname{rand}([1, d]) \\ 0, & \text { else }\end{cases} \end{gathered} \tag{3} D(i)={1,0, if i=rand([1,d]) else (3)
D ( i ) = { 1 , if i = P ( j ) , j ∈ [ 1 , k ] , P = rand ( k ) , k ∈ { 2 , [ r 1 ⋅ ( d − 2 ) + 1 ] } 0 , else (4) D^{(i)}= \begin{cases}1, & \text { if } i=P(j), j \in[1, k], P=\operatorname{rand}(k), \\ k \in\left\{2,\left[r_1 \cdot(d-2)+1\right]\right\} \\ 0, & \text { else }\end{cases} \tag{4} D(i)=⎩ ⎨ ⎧1,k∈{2,[r1⋅(d−2)+1]}0, if i=P(j),j∈[1,k],P=rand(k), else (4)
D ( i ) = 1 (5) D^{(i)}=1 \tag{5} D(i)=1(5)
式中: D ( i ) D^{(i)} D(i) 表示飞行技能; i = rand ( [ 1 , d ] ) i=\operatorname{rand}([1, d]) i=rand([1,d]) 表示生成从 1 到 d d d 的随机整数; rand ( k ) \operatorname{rand}(k) rand(k) 表示创建从 1 到 k k k 的 随机整数排列; r 1 r_1 r1 表示 [ 0 , 1 ] [0,1] [0,1] 之间均匀分布的随机 数; d d d 表示问题维度. 其中 i = 1 , 2 , ⋯ , d i=1,2, \cdots, d i=1,2,⋯,d.
凭借这些飞行技能, 蜂鸟可以访问目标食物源, 从而获得候选食物源. 候选食物源位置更新数学描述 如下:
v i ( t + 1 ) = x i , tar ( t ) + a ⋅ D [ x i ( t ) − x i , tar ( t ) ] (6) v_i(t+1)=x_{i, \text { tar }}(t)+a \cdot D\left[x_i(t)-x_{i, \text { tar }}(t)\right] \tag{6} vi(t+1)=xi, tar (t)+a⋅D[xi(t)−xi, tar (t)](6)
式中: v i ( t + 1 ) v_i(t+1) vi(t+1) 表示第 t + 1 t+1 t+1 次迭代第 i i i 个候选食物源 位置; x i ( t ) x_i(t) xi(t) 表示第 t t t 次迭代第 i i i 个食物源位置; x i , tar x_{i, \text { tar }} xi, tar ( t ) (t) (t) 表示第 i i i 只蜂鸟将访问的目标食物源位置; a a a 表 示服从正态分布 ( ( ( 均值 = 0 =0 =0, 标准偏差 = 1 =1 =1 ) 的引导因子.
依据式 (6), 引导受食第 i i i 个食物源的位置更新 如下:
x i ( t + 1 ) = { x i ( t ) f [ x i ( t ) ] ⩽ f [ v i ( t + 1 ) ] v i ( t + 1 ) f [ x i ( t ) ] > f [ v i ( t + 1 ) ] (7) x_i(t+1)=\left\{\begin{array}{cc} x_i(t) & f\left[x_i(t)\right] \leqslant f\left[v_i(t+1)\right] \\ v_i(t+1) & f\left[x_i(t)\right]>f\left[v_i(t+1)\right] \end{array}\right. \tag{7} xi(t+1)={xi(t)vi(t+1)f[xi(t)]⩽f[vi(t+1)]f[xi(t)]>f[vi(t+1)](7)
式中: x i ( t + 1 ) x_i(t+1) xi(t+1) 表示第 ( t + 1 ) (t+1) (t+1) 次迭代第 i i i 个食物源位 置; f ( ⋅ ) f(\cdot) f(⋅) 表示函数适应度值; 其他参数意义同上.
1.3 区域觅食
蜂鸟在访问了目标食物源后, 很可能会移动到自 己领地外的邻近区域寻找新的食物源, 而不是访问其 他现有的食物源. 邻近区域候选食物源位置更新数学 描述如下:
v i ( t + 1 ) = x i ( t ) + b ⋅ D ⋅ x i ( t ) (8) v_i(t+1)=x_i(t)+b \cdot D \cdot x_i(t) \tag{8} vi(t+1)=xi(t)+b⋅D⋅xi(t)(8)
式中: b b b 表示服从正态分布 ( ( ( 均值 = 0 =0 =0, 标准偏差 = 1 =1 =1 ) 的区域因子; 其他参数意义同上.
1.4 迁徙觅食
当蜂鸟经常造访的区域缺乏食物时, 蜂鸟通常会 迁移到较远的食物来源区进行受食. 花蜜补充率最差 食物源位置更新数学描述如下:
x wor ( t + 1 ) = S L + r ⋅ ( S u − S L ) (9) x_{\text {wor }}(t+1)=S_{\mathrm{L}}+r \cdot\left(S_{\mathrm{u}}-S_{\mathrm{L}}\right) \tag{9} xwor (t+1)=SL+r⋅(Su−SL)(9)
式中: x wor x_{\text {wor }} xwor 表示种群中花蜜补充率最差的食物源位 置; 其他参数意义同上.
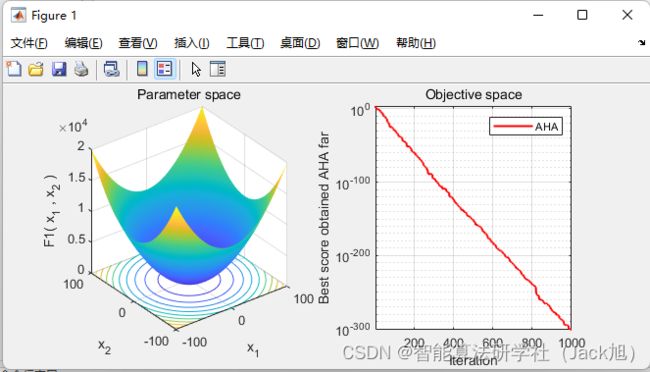
2.实验结果
3.参考文献
[1]Zhao Weiguo,Wang Liying,Mirjalili Seyedali. Artificial hummingbird algorithm: A new bio-inspired optimizer with its engineering applications[J]. Computer Methods in Applied Mechanics and Engineering,2022,388.
[2] 崔东文,袁树堂.基于WPD-AHA-ELM模型的水质时间序列多步预测[J/OL].三峡大学学报(自然科学版):1-8[2022-12-20].DOI:10.13393/j.cnki.issn.1672-948X.2023.01.002.