设计测试用例的方法

设计测试用例的方法有很多，等价类划分法是重点，边界值分析法次之，对于因果图法知道概念就行，老师说考试不会考，但是历年考试中貌似考过一次，这就不知道了，反正考试大题基本课本例题，好像数字都不带换的。猜的，考完别真实我，扫黑除恶请认准 1101 花开富贵，谢谢！

目录

1. 等价类划分法

2. 边界值分析法

3. 因果图法

4. 正交法

5. 场景法

6. 判定表法

7. 决策表法

---

1. 等价类划分法

等价类定义：输入具有代表性的数据子集。

等价类划分法是把所有可能的输入数据，即把程序的输入数据集合划分成若干个子集（即等价类），然后从每一个等价类中选取少数具有代表性的数据作为测试用例。

等价类分为：

① 有效等价类是指完全满足产品规格说明的输入数据，即有效的、有意义的输入数据所构成的集合；

② 无效等价类和有效等价类相反，即不满足程序输入要求或者无效的输入数据构成的集合。

随便举个例子，计算两个1到100之间整数的和。

这时候还用穷举测试吗？

1+2=3，1+3=4  ······ 1+100=101

100+1=101,100+2=102 ······ 100+100=200

你说可以，那我现在换成计算1到1000000之间整数的和，穷举一下？显然不可能，这时候就用到我们的等价类划分法。

有效等价类：满足题目需求的，1 ~ 100之间的整数；

无效等价类：不满足题目需求的，小于1，大于100，非数字，小数。

再比如我们课本上的电话号码的例子，历年题中有考过类似的。

经过类别划分后，每一类的代表性数据在测试中的作用都等价于这一类中的其他值。

2. 边界值分析法

很多时候，我们的错误点往往都是在边界处发生的，为什么呢？

有效数据和无效数据的分界点，往往作为程序员编写程序的判断点，代码编写者一不留神，多写一个等于号或者少写一个等于号，边界处很可能就会出问题了，从而引出边界值分析法。

它是我们目前非常常用的一种黑盒测试用例方法。

什么是边界？

边界是指对于输入等价类和输出等价类而言，稍高于其边界值及稍低于其边界值的一些特定情况。

边界范围：选取正好等于、刚刚好大于或刚刚好小于边界值作为测试数据，每一个边界都要单独作为一个专门的测试用例去编写。

同样还是上边那个例子，计算两个1到100之间整数的和。

正好等于：1，100

刚刚好大于：2，101

刚刚好小于：0，99

特殊边界值：

① 输入域的默认值、空值或空格；

② 报表的第一行、最后一行或第一列、最后一列；

③ 循环的第一次和最后一次；

④ 屏幕上光标移到最右边、最下面等；

⑤ 16 bit 整数的 32767、-32768。

3. 因果图法

通过因果图可以建立输入条件和输出条件之间的逻辑模型，当输入有很多，不同输入的组合对应不同的输出，用因果图来分析不同输入组合和不同输出之间的关系。

因果图法设计测试用例的步骤：

①分析出所有的输入输出；

②找出输入输出之间的关系；

③根据输入输出之间的关系画因果图；

④根据因果图画判定表；

⑤根据判定表设计测试用例。

因果图举例：

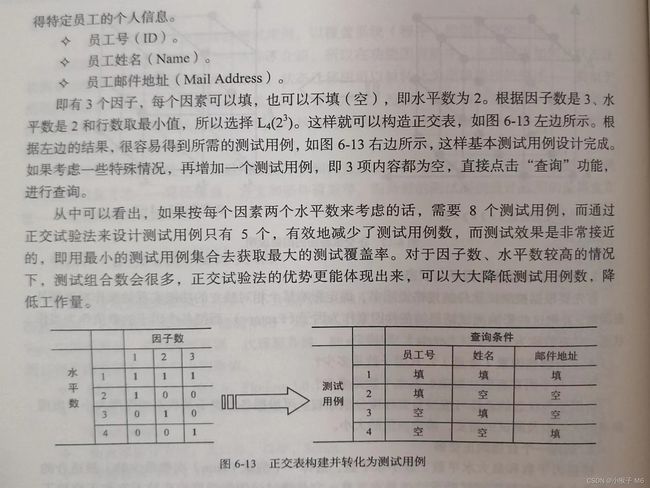
4. 正交法

使用步骤：

① 根据需求形成因子状态表（因子 → 控件名称，状态 → 每个控件对应的取值）；

② 确定所采用的正交表；

③ 将正交表中的字母用文字代替；

④ 一行就是一条测试用例。

应该不考，了解即可。

5. 场景法

基本流：按照正确的业务流程操作的一种途径；

备选流：出现错误的操作流程。

场景法设计测试用例的步骤：

① 确定项目角色（前台用户、后台用户）；

② 明确角色的常用功能；

③ 根据需求构建测试场景；

④ 一个场景就是一条 case。

举个例子，用户进入一个在线购网站进行购物，选购物品后，进行在线购买，这时需要使用账号登录，登录成功后，进行付钱交易，交易成功后，生成订购单，完成整个购物过程。

这里仅展示部分场景，实际上你能想象到的每个场景都要写出来。 

6. 判定表法

案例如下，若用户欠费或者关机，则不允许主被叫。

 适用范围：题目条件中有多个输入和多个输出，输入和输入之间有相互的组合关系，而且输入和输出之间有相互的制约和依赖关系。

7. 决策表法

决策表方法就是对多个条件的组合进行分析，从而设计测试用例来覆盖各种组合，决策表从输入条件的完全组合来满足测试的覆盖率要求，具有严格的逻辑性，所以基于决策表的测试用例设计方法是最严格的，测试用例具有很高的完整性。

条件桩：列出问题的所有条件；

动作桩：列出可能针对问题所采取的操作；

条件项：针对所列条件的具体赋值；

动作项：列出在条件项组合情况下应该采取的动作。

具体步骤：

① 列出所有的条件桩和动作桩；

② 填入条件桩；

③ 填入动作桩；

④ 简化、合并相似规则或者相同动作。

课本实例

根据输人3条边（a、b、c）边长的值来判断是否构成一个三角形，如果是三角形，继续断是等腰三角形还是等边三角形等。为了使问题简单些，假定 a、b、c 只能输人大于零的数不需要考虑 a、b、c 取零或负数的情况。

分析：根据3条边，判断是否能构成三角形，只要两条边之和大于第3边。然后在判断是否有两条边相等，是否所有两条边都相等，从而决定是等腰三角形还是等边三角形。所以共有6个条件---a+b>c、a+c>b、b+c>a、a=b、b=c、a=c;而动作(结果显示)有4个 —— 非三形、不等边三角形、等腰三角形、等边三角形。而且，根据一些规则和推理可以简化组合。

如果不能构成三角形，则不需要判断后3个条件。
如果构成三角形，即 a+b>c、a+c>b 和 b+c>a 都必须成立，没有例外。
如果 a=b 且 a=c，则 b=c 肯定成立。
如果 a=b，而 a=c 不成立，就不需要判断 b=c，实际上 b=c 也肯定不能成立，只能为等腰三角形。

这样可以大大简化，将64种组合降低到8种组合，形成非常优化的决策表，每一列构成一个规则，设计相应的测试用例覆盖各项规则，即覆盖表中各列。