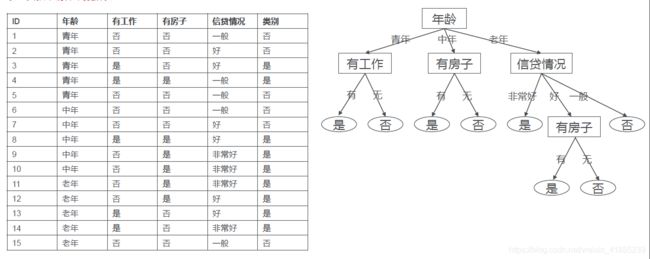
决策树(decision-tree)原理和实现
decision_tree(决策树)
决策树算法是通过对训练数据集进行不断的分类,最终建立起来的决策树。
既然是建立一棵树,自然就下如何划分根节点和叶子节点,如何建立左子树和右子树等问题。
如何建立决策树
节点是什么
每个节点表示一个特征。
每个节点如何选择
其实这个问题最终就是一个问题:就是如何选择根节点,因为其他的节点也是子树的根节点,所以只要搞明白根节点是选择标准,就一切好说。在决策树中,是通过信息增益(ID3算法),信息增益率(C4.5)或者是基尼系数(CART算法)来进行根节点的选择,每一种标准对应一种算法。
ID3算法
ID3算法是根据信息增益来进行根节点选择的,下面介绍一下信息增益的计算和原理
熵
H ( p ) = − ∑ i = 1 n p i l o g p i H(p)=-\sum_{i=1}^{n}p_{i}log p_{i} H(p)=−i=1∑npilogpi
以上的熵的计算公式, p i p_{i} pi表示最终决策结果的概率,那上面数据集举例子来说,结果只有两种种类,就是可以贷款(是),或者不可贷款(否)。所以概率只有两种。
假设可以贷款的概率是 p 1 p_{1} p1,不可贷款的概率是 p 2 p_{2} p2,此时的熵为:
H ( p ) = − 9 15 lg 2 9 15 − 6 15 lg 2 6 15 H(p)=-\frac{9}{15}\lg_{2}{\frac{9}{15} }- \frac{6}{15}\lg_{2}{\frac{6}{15} } H(p)=−159lg2159−156lg2156
条件熵
顾名思义,就是在固有条件的基础上计算熵的大小,首先熵的计算思路是不变的,熵永远是基于结果进行计算,差别只是在于数据集的不同,这里既然是条件熵,自然是在某个条件下的那部分数据集进行基于结果的熵计算。
H ( Y ∣ X ) = ∑ i = 1 n p i H ( Y ∣ X = x i ) H(Y\mid X)=\sum_{i=1}^{n}p_{i}H(Y\mid X=x_{i} ) H(Y∣X)=i=1∑npiH(Y∣X=xi)
例如计算你年龄的条件熵
H ( Y ∣ 年 龄 ) = − ( 5 15 ( − 2 5 log 2 2 5 − 3 5 log 2 3 5 ) + 5 15 ( − 3 5 log 2 3 5 − 2 5 log 2 2 5 ) + 5 15 ( − 4 5 log 2 4 5 − 1 5 log 2 1 5 ) ) H(Y\mid 年龄)=-(\frac{5}{15}(-\frac{2}{5}\log_{2}\frac{2}{5}- \frac{3}{5}\log_{2}\frac{3}{5})+ \frac{5}{15}(-\frac{3}{5}\log_{2}\frac{3}{5}- \frac{2}{5}\log_{2}\frac{2}{5})+\frac{5}{15}(-\frac{4}{5}\log_{2}\frac{4}{5}- \frac{1}{5}\log_{2}\frac{1}{5})) H(Y∣年龄)=−(155(−52log252−53log253)+155(−53log253−52log252)+155(−54log254−51log251))
信息增益
信息增益就是等于熵减去条件熵
g(D, A) = H(D) − H(D | A)
算法流程
就是通过计算每个条件的信息增益,增益最大的选作根节点,其他的作为子树存在,在子树中同样采用计算信息增益的方法。逐步递归直到建立一个决策树。
C4.5算法
此算法与ID3区别在于,用的不是信息增益,而是信息增益率。
g R ( D , A ) = g ( D , A ) H A ( D ) g_{R}(D,A)=\frac{g(D,A)}{H_{A}(D) } gR(D,A)=HA(D)g(D,A)
其中
H A ( D ) = − ∑ i = 1 n ∣ D i ∣ ∣ D ∣ log 2 ∣ D i ∣ ∣ D ∣ H_{A}(D)=-\sum_{i=1}^{n}\frac{\left | D_{i} \right | }{\left | D \right | }\log_{2}{\frac{\left | D_{i} \right |}{\left | D \right | } } HA(D)=−∑i=1n∣D∣∣Di∣log2∣D∣∣Di∣
其实就是在信息增益的基础上,除以一个基于条件的熵,而不是基于结果的熵。
CART算法
此算法与上面的区别在于,划分根节点的技术是用基尼系数进行划分,划分后建立起来的是二叉树。
G i n i ( p ) = ∑ k = 1 k p k ( 1 − p k ) = 1 − ∑ k = 1 k p k 2 Gini(p)=\sum_{k=1}^{k}p_{k}(1-p_{k}) =1-\sum_{k=1}^{k}p_{k} ^{2} Gini(p)=k=1∑kpk(1−pk)=1−k=1∑kpk2
注意基尼系数和熵意义,也是基于结果计算的。
条件基尼系数:
G i n i ( D , A ) = ∣ D 1 ∣ ∣ D ∣ G i n i ( D 1 ) + ∣ D 2 ∣ ∣ D ∣ G i n i ( D 2 ) Gini(D,A)=\frac{\left | D_{1} \right | }{\left | D \right | } Gini(D_{1})+\frac{\left | D_{2} \right | }{\left | D \right | } Gini(D_{2}) Gini(D,A)=∣D∣∣D1∣Gini(D1)+∣D∣∣D2∣Gini(D2)
与信息增益不同,这里要选择条件基尼系数最小的作为根节点。
剪枝
剪枝操作,有预剪枝和后剪枝,目的是为了防止过拟合,具体操作如下
预剪枝(在训练中完成)
1.首先不对节点进行决策树划分,然后利用测试集进行准确度计算。
2.进行决策树划分,然后利用测试集进行准确度计算。
3.比较1和2中的准确度,如果未划分时准确度高,怎不进行再次的划分,反之则继续对其进行子树划分。
后剪枝(在建立好的决策树的基础上)
1.去掉某个子节点上的所有叶子节点,计算模型的准确度。
2.不去掉任何节点,计算准确度。
3.如果1的准确度高于2,则进行剪枝,反之不剪枝。
ID3示例代码
# coding=utf-8
from math import log
import operator
def loaddata():
dataSet = [[1, 0,0,0, 'no'],
[1, 0,0,1,'no'],
[1, 1,0,1, 'yes'],
[1, 1,1,0, 'yes'],
[1, 0,0,0, 'no'],
[2, 0,0,0, 'no'],
[2, 0,0,1, 'no'],
[2, 1,1,1, 'yes'],
[2, 0,1,2, 'yes'],
[2, 0,1,2, 'yes'],
[3, 0,1,2, 'yes'],
[3, 0,1,1, 'yes'],
[3, 1,0,1, 'yes'],
[3, 1,0,2, 'yes'],
[3, 0,0,0,'no']]
labels = ['age','job','house','credit']
return dataSet, labels
#计算数据集的熵
def entropy(dataSet):
m = len(dataSet)
labelCounts = {}
for featVec in dataSet:
currentLabel = featVec[-1]
if currentLabel not in labelCounts.keys(): labelCounts[currentLabel] = 0
labelCounts[currentLabel] += 1
e = 0.0 #熵
for key in labelCounts:
prob = float(labelCounts[key])/m#求得是和否的概率
e -= prob * log(prob,2)#熵值计算
return e
#根据特定特征中的特定属性进行子集划分
def splitDataSet(dataSet, axis, value):
retDataSet = []
for featVec in dataSet:
if featVec[axis] == value:
reducedFeatVec = featVec[:axis]
reducedFeatVec.extend(featVec[axis+1:])
retDataSet.append(reducedFeatVec)
return retDataSet
#选择最好的特征,本质其实就是计算信息增益
def chooseBestFeature(dataSet):
n = len(dataSet[0]) - 1#特征数
baseEntropy = entropy(dataSet)
bestInfoGain = 0.0; bestFeature = -1
for i in range(n): #遍历每个特征
featList = [example[i] for example in dataSet]#获取当前特征的所有值
uniqueVals = set(featList) #当前特征的可能取值
newEntropy = 0.0
for value in uniqueVals:
subDataSet = splitDataSet(dataSet, i, value)
prob = len(subDataSet)/float(len(dataSet))
newEntropy += prob * entropy(subDataSet)
infoGain = baseEntropy - newEntropy #计算信息增益
if (infoGain > bestInfoGain):
bestInfoGain = infoGain
bestFeature = i
return bestFeature
#类别的投票表决
def classVote(classList):
classCount={}
for vote in classList:
if vote not in classCount.keys(): classCount[vote] = 0
classCount[vote] += 1
sortedClassCount = sorted(classCount.iteritems(), key=operator.itemgetter(1), reverse=True)
return sortedClassCount[0][0]
#训练一棵树
def trainTree(dataSet,labels):
classList = [example[-1] for example in dataSet]
if classList.count(classList[0]) == len(classList):
return classList[0]#所有类别都一致
if len(dataSet[0]) == 1: #数据集中只剩下一个特征
return classVote(classList)
bestFeat = chooseBestFeature(dataSet)
bestFeatLabel = labels[bestFeat]
myTree = {bestFeatLabel:{}}
# del(labels[bestFeat])
featValues = [example[bestFeat] for example in dataSet]
uniqueVals = set(featValues)
for value in uniqueVals:
subLabels = labels[:]
myTree[bestFeatLabel][value] = trainTree(splitDataSet(dataSet, bestFeat, value),subLabels)
return myTree
#本质就是遍历树,最终取到对应的叶子节点。
def predict(inputTree,featLabels,testVec):
firstStr = list(inputTree.keys())[0]
secondDict = inputTree[firstStr]
featIndex = featLabels.index(firstStr)
key = testVec[featIndex]
valueOfFeat = secondDict[key]
if isinstance(valueOfFeat, dict):
classLabel = predict(valueOfFeat, featLabels, testVec)
else: classLabel = valueOfFeat
return classLabel
myDat,labels = loaddata()
# print(chooseBestFeature(myDat))
myTree = trainTree(myDat,labels)
print(myTree)
print(predict(myTree,labels,[1,1,0,1]))
注:
1.如何理解信息增益?我个人理解的信息增益可以理解为这条信息对一个决策的作用大小,如果起到的作用大,信息增益就大。
2.何时用ID3,ID3对特征中属性种类较多时有所偏好,所以当某个特征中属性比较多时,不宜采用。
3.合适用C4.5,功能恰好与ID3相反。
4,何时用CARD,目前用最多的都是此算法,至于什么场合,我也不太清楚。