粒子群（PSO）求方程最优解

PSO

PSO类似于雷达扫描，每一个粒子就像觅食的狗一样，闻到了100米范围内有食物，但是却并不知道食物具体在那里。这个时候就需要找一群狗来共同寻找食物，这个群体的数量就是粒子群的粒子个数。
扩大这个范围，当食物在天上时，狗的二维探测能力就无法满足，这时粒子就变成鸟，仍然在给定的范围内寻找食物。一般来说，粒子数量越大越容易找到食物（相对最优解），但是过大的粒子个数会消耗巨大的资源，我们需要根据具体问题，分析得到最优种群个数。

解方程

本文用解方程最优解的形式来展示粒子群收缩求最优解的过程
解一个大家都认识的方程：

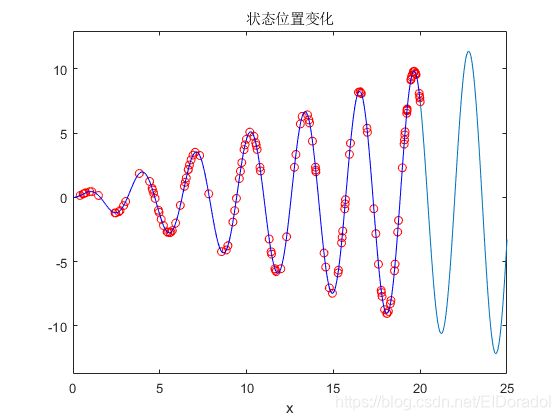
利用ezplot函数画出粒子不断在一维函数图像上收敛的过程。

f（x）=x*sin(x)*cos(x)

模型的参数设置

//模型的参数设置
N = 70;                         // 初始种群个数
d = 1;                          // 空间维数
ger = 100;                      // 迭代次数     
limit = [0, 20];                // 设置位置参数限制
vlimit = [-1, 1];              //设置速度限制
w = 0.6;                        //惯性权重
c1 = 0.4;                       //自我学习因子
c2 = 0.45;                       //群体学习因子 

随机生成粒子的位置

x = limit(i, 1) + (limit(i, 2) - limit(i, 1)) * rand(N, d);

代入方程算出粒子当前的适应度并记录，当迭代ger次后，即可得到粒子迭代100次的最佳适应度，并求出x。

[fym, nmax] = max(fxm);   
        ym = xm(nmax, :); 

对超出边界值的速度进行限制。此处因为是一维的，只要把可能超过边界的速度值用边界值代替就行了。代替的方法就是赋值，怎么赋值，方法有很多。

vlimit = [-1, 1];

完整代码

f= @(x)x .* sin(x) .* cos( x); % 函数表达式
figure(1);
ezplot(f,[0,0.001,25]);
N = 70;                         % 初始种群个数
d = 1;                          % 空间维数
ger = 100;                      % 迭代次数     
limit = [0, 20];                % 设置位置参数限制
vlimit = [-1, 1];               % 设置速度限制
w = 0.6;                        % 惯性权重
c1 = 0.4;                       % 自我学习因子
c2 = 0.45;                       % 群体学习因子 
for i = 1:d
    x = limit(i, 1) + (limit(i, 2) - limit(i, 1)) * rand(N, d);%初始种群的位置
end
v = rand(N, d);                  % 初始种群的速度
xm = x;                          % 每个个体的历史最佳位置
ym = zeros(1, d);                % 种群的历史最佳位置
fxm = zeros(N, 1);               % 每个个体的历史最佳适应度
fym = -inf;                      % 种群历史最佳适应度
hold on
plot(xm, f(xm), 'ro');title('初始状态');
figure(2)
%% 群体更新
iter = 1;
record = zeros(ger, 1);          
while iter <= ger
     fx = f(x) ; % 个体当前适应度   
     for i = 1:N      
        if fxm(i) < fx(i)
            fxm(i) = fx(i);     % 更新个体历史最佳适应度
            xm(i,:) = x(i,:);   % 更新个体历史最佳位置
        end 
     end
if fym < max(fxm)
        [fym, nmax] = max(fxm);   % 如果说粒子小于我们开始给定的范围，更新位置
        ym = xm(nmax, :);      % 存储
 end
    v = v * w + c1 * rand * (xm - x) + c2 * rand * (repmat(ym, N, 1) - x);% 复制ym矩阵
    % 边界速度处理
    v(v > vlimit(2)) = vlimit(2);
    v(v < vlimit(1)) = vlimit(1);
    x = x + v;% 位置更新
    % 边界位置处理
    x(x > limit(2)) = limit(2);
    x(x < limit(1)) = limit(1);
    record(iter) = fym;%最大值记录
     x0 = 0 : 0.01 : 20;
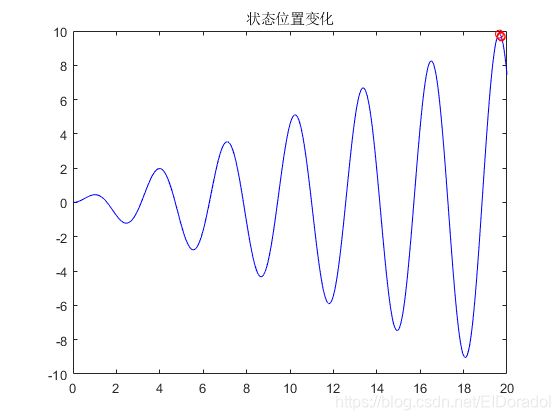
     plot(x0, f(x0), 'b-', x, f(x), 'ro');title('状态位置变化')
     pause(0.1)
    iter = iter+1;
end
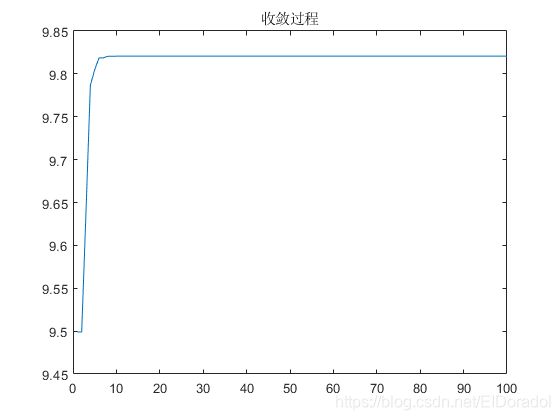
figure(3);plot(record);title('收敛过程')
x0 = 0 : 0.01 : 20;
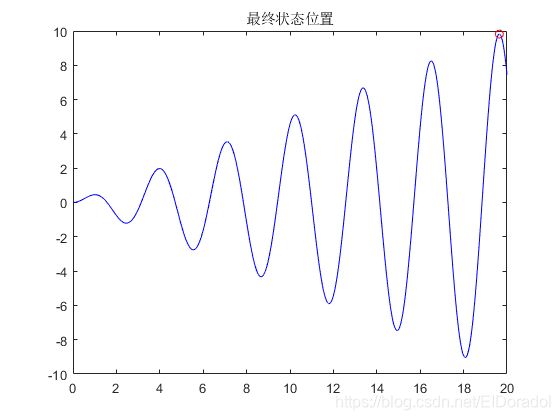
figure(4);plot(x0, f(x0), 'b-', x, f(x), 'ro');title('最终状态位置')
disp(['最大值：',num2str(fym)]);
disp(['变量取值：',num2str(ym)]);

结果如图所示：

收敛结果

最大值：9.8207
变量取值：19.6477