推荐系统学习(九)
ConvNCF-2018年IJCAI
- 概述
-
- 作者及论文
- 前人研究
-
- MF
- 本文模型
-
- NCF模型
-
- Input layer
- Emdedding layer
- Hidden layer
- Prediction layer
- 损失函数
- 评价指标
- 创新点
- 代码
- 参考资料
概述
作者及论文
这篇作者与上一篇一样都是何向南博士的论文,提出了一种新颖的解决方法
Outer Product-based Neural Collaborative Filtering
当然代码和PPT、以及论文都可在他的主页上找到。
前人研究
MF
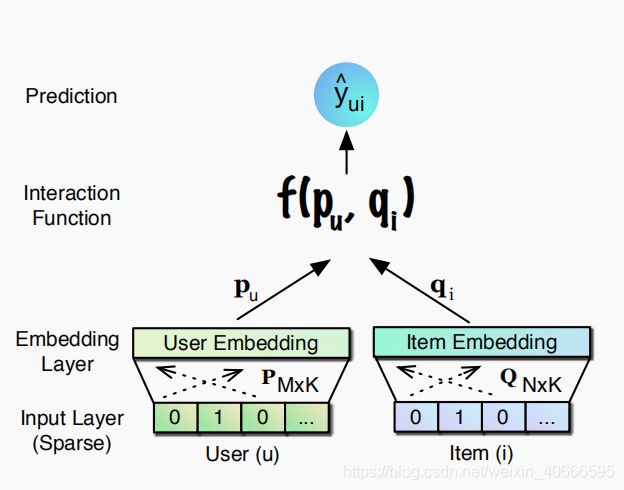
MF大家一定很熟悉了如上图,上一篇也有简单的说明,这块我主要是进一步谈一下MF的弊端:
- MF使用 Inner Products 作为交互函数,(上一篇讨论过)
- MF用 Inner Products 其实有一个隐含条件,Embedding(表征user或者item作为一个latent factors) dimensions 之间是相互独立的,但是这个假设是不切合实际的,[Zhang et al., SIGIR’14]证明了其没必要是独立的。
那么如何建立Embedding dimensions之间的关系模型??
- 引入外积的概念,user和item embedding成对的交互形成特征矩阵
- 在特征交互的矩阵上采用 CNN,从局部和全局,对每个维度进行高阶的交互
本文模型
推荐系统问题是在 IR (信息检索)领域中很重要的研究方向,而协同过滤方法又是最为常用且有效地推荐算法和模型。一个协同过滤模型主要有两部分:使用特征向量表示用户和物品;特征向量的交互计算,即用户对物品的感兴趣程度。(注:表示学习得到用户、物品的特征向量 p p p 和 q q q,而模型设计中,学习一个打分函数 f : ( R n , R n ) → R f:(R^n,R^n)→R f:(Rn,Rn)→R。)因此,在引入神经网络模型后,大部分工作都在如何学习更好的表示和交互模型的构建上。
本文指出了目前较为流行的各种MF及其变体模型大多采用特征向量内积、拼接操作的局限性。为此,提出了一种基于外积(Outer product)的新的特征交互模型,通过特征交互操作得到一个特征矩阵(类似与图片),在此基础上应用 CNN 学习到特征中每一维的高阶相互关系。
NCF模型
本文提出了一种新的 NCF 模型,意在模型中融合一种特征维度之间的关系。具体而言,就是通过特征向量的外积,得到交互矩阵(Interaction Map) E ∈ R K × K E∈R^{K×K} E∈RK×K,K 是特征向量维数。如此构建的交互矩阵,体现出了每个维度下特征之间的关系,而其中也包含了传统 CF 的内积信息(E 中的主对角线求和即为向量内积),最终能刻画特征维度之间的高阶关系。此外,在特征矩阵上引入 CNN 处理方式,也比全连接 MLP 更容易泛化、也更容易建立更深的网络。

Input layer
ONCF 模型的输入是一个用户、物品对 u 和 i,输入层是一个 one-hot 编码的向量.
Emdedding layer
通过一个 embedding 映射 P P P 和 Q Q Q 得到一个表示 p u p_u pu 和 q i q_i qi,计算外积,得到 Interaction Map E = p u ⊗ q i = p u q i T E=p_u⊗qi=p_uq^T_i E=pu⊗qi=puqiT 矩阵。与一般方法相比,具有三个优势:
- 对于矩阵分解的方法是一种泛化,矩阵分解只使用了 E 的主对角元素;
- 比矩阵分解考虑到了更多的每一个特征维度之间的关系;
- 比特征向量的拼接更有可解释性,是从一个综合的角度来看建模的。
与此同时,相关的实践经验表示,这样的特征之间的交互操作,更有利于深度模型的学习。(注:作者团队提出过 NFM 模型验证)另一方面, E E E 是一个二维矩阵,与(单通道)图片是类似的,CNN 操作尤其能够抓住这个矩阵中的局部、全局信息特征。
Hidden layer
输入是交互矩阵 E E E,输出则是隐藏状态 g = f Θ ( E ) g=f_\Theta(E) g=fΘ(E),其中 f Θ f_\Theta fΘ 是一个从矩阵到向量的映射, Θ \Theta Θ 是模型参数。在这个模型中,是一个 CNN 结构。
在这里用CNN,优点在于:
-
CNN相比MLP有较少的参数
-
Hierarchical tower structure:高层集成了更多的信息。
-
最终预测总结了交互地图中的所有信息。
对于这里的 E E E,可以使用一个 MLP 对向量化(拉直操作)的 E E E 处理和运算。可是这样做带来的问题是:如果 E E E 的规模是 K × K K×K K×K,取 K=64,那么 e = v e c ( E ) e=vec(E) e=vec(E) 是一个 64×64=4096 的特征向量,那么标准的第一层 MLP 的权重就已经至少是 4096×2048 的规模了,这样的参数规模是可怕的:需要极其庞大的计算资源和开销、需要更多的数据来拟合参数、调参问题。

-
输入的是一个 K × K K×K K×K 的矩阵 E,图中假设 K=64
-
模型一共有 6 层,每一层都有 32 个 Feature Map,每个卷积核都是 2×2 的,那么每一层过后,Feature Map 的两个维度都缩小为上一层的一半,激活函数选择 RELU
-
最后输出第六层是一个 1×1×32 的张量,可以视作一个向量 g,即为隐藏层的输出
-
从参数规模上,比第一层的 MLP 就要小了几百倍,因此在数据不太多的情况下,具有更好的稳定性和泛化能力。
Prediction layer
计算预测得分 y u i = w T g y_{ui}=w^Tg yui=wTg,至此,整个模型需要学习的参数有 P , Q , Θ , w P,Q,\Theta,w P,Q,Θ,w
损失函数
模型的损失函数是一个 B P R BPR BPR 损失,能够刻画观测到的正例比负例有更高的得分排名:
L ( Δ ) = ∑ ( u , i , j ) ∈ D − ln σ ( y ^ u i − y ^ u j ) + λ Δ ∣ Δ ∣ 2 L(\Delta) = \sum\limits_{(u,i,j) \in \mathcal{D}} - \ln \sigma(\hat{y}_{ui} - \hat{y}_{uj}) + \lambda_\Delta |\Delta|^2 L(Δ)=(u,i,j)∈D∑−lnσ(y^ui−y^uj)+λΔ∣Δ∣2,其中 D : = ( u , i , j ) ∣ i ∈ Y u + ∧ j ∉ Y u + \mathcal{D} := {(u,i,j) | i \in \mathcal{Y}_u^+ \wedge j \notin \mathcal{Y}_u^+} D:=(u,i,j)∣i∈Yu+∧j∈/Yu+, Y + Y^+ Y+ 是用户 u u u 观测到的正例。
值得一提的是,预测层参数 w w w 的等比例放大,会增大 ( y ^ u i − y ^ u j ) (\hat y_{ui} − \hat y_{uj}) (y^ui−y^uj) 的值,体现在训练过程中,会使得 w w w 的分量值较大,因此需要引入 L 2 L_2 L2 或者是 maxnorm 的限制。
评价指标
作者给出了一些直观上的说明,在从前一层去往后一层的过程中,后一层的每一个元素都是由前一层的 4 个元素计算得来的,可以认为是一个 4 阶关系的刻画。直到最后的输出层,降到 1×1 后,即包含了特征每一个维度之间的交互信息。
与上一篇的评价指标一样HR@10 和 NDCG@10
创新点
其实还在于user-item的交互是变成外积,抽取特征用图卷积的方式
代码
待更新!!!
参考资料
vector - vector product
落尽红樱君不见,轻绘梨花泪沾衣
这是我研究生期间读的所有关于RS的论文,RS呢也是兴趣所在,这个领域好的论文特别多,希望之后有机会继续更新。