基于图像的三维重建——基于空间patch扩散的方法(PMVS)
1.PMVS:多视图匹配经典算法简介
导语:常见的稠密重建方法主要有三种:基于体素的方法、基于深度图融合的方法以及基于3D patch扩张的方法。第一种基于体素的方法仅适用于小场景,单个物体,遮挡较少的情况,不予赘述。第二种基于深度图融合的方法在前面已经介绍过:基于图像的三维重建——深度图计算方法1-SGM/tSGM(9)以及基于图像的三维重建——深度图计算方法2-PatchMatch(10),这两种都是通过计算得到的不同视角的深度图进行融合来获取稠密点云。而今天要介绍的就是第三种方法:基于3D patch扩张的方法,PMVS就是其中的典型算法,主要以已知内外参数的多幅图像(sfm的结果)为输入,重建出真实世界中物体/场景的三维模型。
论文题目:Accurate,Dense,and Robust Multiview Stereopsis.

代码地址:https://github.com/pmoulon/CMVS-PMVS
算法效果:如下所示,从左到右一次为输入图像(不同角度共48张),特征点提取,特征匹配结果,扩张剔除迭代3次后效果,转换为网状模型效果。

2.基本模型
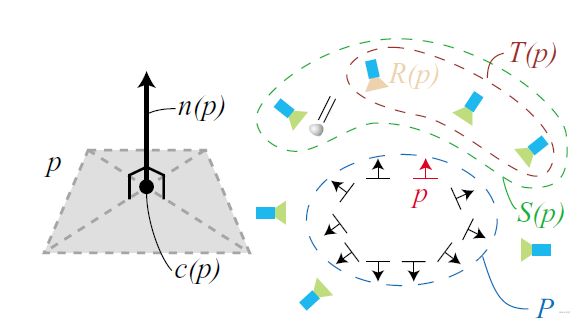
基本模型中提及的符号含义:
| p | patch | 面片 |
|---|---|---|
| c( p ) | the center of patch | 面片中心 |
| n( p ) | unit normal vector oriented toward the cameras observing it | 面片朝向摄影中心的单位向量 |
| R( p ) | a reference image in which p is visible | 某一可以看到面片的参照图像 |
| O( Ii ) | the optical center of the corresponding camera | 图像Ii对应的摄影中心 |
| V( p ) | a set of images in which p is visible | 可以看到某一面片的所有图像集合 |
| Ci( x,y ) | a regular grid of β \beta β× β \beta β pixels cells | 图像Ii在(x,y)处 β \beta β× β \beta β 大小的网格单元 |
| Qi( x,y ) | the set of patches of Ci(x,y) | Ci(x,y)处的面片集 |
面片模型:
所谓面片,是指三维物体表面的局部切平面,可以近似地表示某一局部范围内地三维物体表面,与数学中在某一范围内用切线研究曲线的做法一致,都是“非线性函数线性化来近似处理”的思想。本质上看,一个面片是三维空间中的一个矩形,由其中心点、单位法向和参考图像三者共同确定,中心点 c( p )是其对角线交点的坐标,单位法向 n( p )是从中心点指向参考图像 R( p)对应的摄影中心的单位向量,这里之所以要引入参考图像的概念,是因为一个面片会在多幅图像中出现,选定其中的某一图像作为该面片的参考图像,将包含该面片的所有图像组成的集合 V( p )称为该面片的可视集。
成像差异函数:
接着作者在可视集的基础上引入了成像差异函数(Photometric Discrepancy Function)的概念,或者叫灰度差异函数。

其中,V( p ) \ R( p )表示,面片p的可视集V( p )除去参考图像R( p )外其他图像的集合,|V( p ) \ R( p )|表示该集合中图像的个数,也就是出现面片p的图像个数减一。
要想理解g( p )函数,要先明白h( p )函数的意思,而这里的h( p )函数也是一个成像差异函数,h(p,I1,I2)表示图像I1和I2之间的成像差异。两个函数建立的基础不一样,g( p )是建立在某一面片的可视集上,包括两张及两张以上图像,h( p )是针对两张图像而言的。总的来说,两者的关系如下,h( p )函数是g( p )函数|V( g )| = 2时的特殊情况,计算g( p )是通过对多个h( p )求和得到的。成像差异函数如下图所示:

其中h(p,I1,I2)的计算分为以下三个步骤:
1.在面片p上铺设 μ \mu μ× μ \mu μ大小的网格(该文使用5×5或者7×7);
2.以5×5为例,将25个像点投影在图像I上,通过双线性函数内插出灰度值,记为q(p,Ii);
3.用1减去q(p,I1)和q(p,I2)间的归一化互相系数NCC,相关系数是反应两者间相关程度的,经过归一化后位于0到1之间,用1减去该值得到反映两者之间的差异程度h(p,I1,I2),同样h( p )也在0到1之间。
由于g( p )对于图像中出现高光或者有障碍物的情况下的效果不好,因此在实际情况下,我们需要保证图像I和图像R( p )的灰度一致性函数大于一定的α。因此有:

面片的优化:
面片优化的目的是恢复那些g*( p )较小的面片,每个面片的重建过程分为以下两步:
1.初始化面片的相关参数c( p ),n( p ),V*( p )和R( p );
2.优化c( p )和 n( p )。
几何参数c( p )和n( p )的优化是通过最小化g*( p )而得到的。为了简化计算,将c( p )约束在某一条光线上,这样p在其对应的可视图集V*( p )中某个图像的投影位置就不会变,因此降低了p的自由度。n( p )是由欧拉角决定的,可以用共轭梯度法求解这个优化问题。
图像模型:
基于面片的表面表示方式最大的优势是其灵活性,但缺少面片与面片之间的连接信息,这使得寻找临近面片,面片规整操作实现起来比较复杂,为此引入图像模型(Image Model),建立重建出面片和其可视图像上投影间的联系。具体的讲,将每张图片分割为 β \beta β× β \beta β的网格单元Ci(x,y),这里的x,y表示图像块的下标,i表示这是第i张图像的。给定一个面片p和对应的V( p ),把p投影到V( p )的图像中,以得到面片p对应的图像块,每个图像块Ci(x,y)用一个集合Qi(x,y)记录了所有投影到这个图像块的面片,同理,我们用Qi*(x,y)来表示V*( p )得到的结果。如下图所示:

3.初始面片生成
该论文提出的多视图匹配三维重建方法,可以分为初始面片、面片扩展、面片剔除三部分,经过初始特征匹配得到一组稀疏的面片集合,然后通过反复扩展、剔除面片的过程得到最终的结果。每幅图像通过Harris和Dog算子提取处特征点后,进入到特征匹配阶段,这是PMVS算法的核心内容,思路如下:
1)核线约束,对于图像Ii上的每个特征点f都关联一个数组F,其中包括其他图像上位于同名核线上的所有特征点,而且是同种类型的特征点,即同为Harris特征点或者Dog特征点;
2)前方交会,从F中选取出一个特征点f’,构成一对同名像点(f,f’),通过三角测量中的前方交会,求出物方点三维坐标;
3)点转面片,初始化面片的三个基本属性,物方点坐标作为c( p ),图像Ii作为参考图像,物方点坐标与摄影中心连线方向构建出单位法向量n( p );
4)确定可视集,通过物方点和其他摄影中心连线与其单位法向量间的夹角确定可视集V( p ),这里存在一个阈值t,在该文中取为Π/3,即正负60度范围内。在可视集的基础上进一步确定出更新可视集V*( p ),这里存在另一个阈值α,文中这里取为0.6,即与参考图像间的成像差异系数h(p,I,R( p ))要小于0.6;一旦更新可视集V*( p ),那么该面片的总成像差异函数g*( p )也就确定下来了;
5)优化面片位姿,以最小化面片的总成像差异函数g*( p )为目标,通过共轭梯度法,改正面片的位置和姿态,为了简化计算,文中讲描述物体在三维空间中位置姿态的6个位置数简化为3个,分别是深度、俯仰角和航向角,限制了在射线上移动,所以只有Z方向在改变,不考虑横滚角是因为面片模型规定了面片的某条边要与相机的x轴平行;
6)存储面片,面片的位姿改变后,相关联的更新可视集V*( p )也会随之改变,这里的阈值α取为0.3,如果此时更新可视集V*( p )中的图像个数大于阈值 γ \gamma γ,那就意味着该面片至少出现 γ \gamma γ个低成像差异的图像上,该面上重建成功,将其存储在对应的网格单元出,更新Qi(x,y),Q*(x,y)。

4.面片扩展
经过上述的特征匹配后,重建出了一组稀疏的面片,接下来通过已有的面片在周围空处生成新的面片进行扩展,期望达到的效果是每个图像网格单元上都至少包含有一个面片。首先,对于一个面片p,明确其周边可以扩张的网格单元,然后按照某种扩展策略进行扩展,具体步骤如下:
确定可扩展网格单元:
存在面片p的网格单元Ci(x,y),根据下式,将其上下左右四个网格单元视作临近网格单元,但并非每个临近网格单元都是可扩张的网格单元,还需要满足两个基本条件。

第一个条件是:该网格单元中不存在邻近面片p’,邻近面片的判定条件如下,意思就是说两个面片中心点的距离不能过大,且两个面片的朝向不能偏差很大。

第二个条件是作者从深度方面考虑的,扩张出的面片p和面片p对应的实际深度不能相差过大,但是实际的深度要在完成三维重建的过程才能知道,这里就进入到了一个“鸡生蛋”的逻辑死循环,该论文中作者在这里仅做了一个简单地处理,判断两者间的成像差异函数。
结合下图总结如下:在确定可扩张的网格单元时分为三种情况,没有面片时(绿色箭头a)进行扩张;有面片且为邻近面片时(红色箭头b)没有必要扩张;有面片但非邻近面片时(橙色c)需要进一步判断成像差异函数,若小于给定阈值没有必要扩张,大于给定阈值则扩张。

扩展策略:
在明确了哪些网格可以扩展后,接下来的问题就是如何根据已有的面片构建出新的面片了,思路如下:
1)初始化属性,初始化面片p’的c(p’)、n(p’)和V(p’)属性,直接用面片p的n( p )、R( p )和V( p )属性作为p’的初值,只有c(p’)不同,c(p’)取通过参考图像的摄影中心和网格单元中心连线与面片p所在的平面的交点,再从V(p’)中求得V*(p’);
2)优化面片位姿,知道了更新可视集V*(p’),那么该面片的总成像差异函数g*(p’)也就确定下来了,与特征匹配中的优化方法类似,以最小化面片的总成像差异函数g*(p’)为目标,通过共轭梯度法,改正面片的位置和姿态,这里同样限制为3个自由度;
3)添加可视图像,因为面片p’跟p是不同的,所有先前直接将p的可视集作为p’的可视集是可以进一步改进的,这里通过视差图测试向V(p’)添加新的图像,然后再次从V(p’)求出V*(p’);
4)存储面片,如果此时更新可视集V*(p’)中的图像个数大于阈值 γ \gamma γ,那就意味着该面片至少出现在 γ \gamma γ个低成像差异的图像上,该面片重建成果,将其存储在对应的网格单元处,更新Qi(x,y)和Qj*(x,y)。

5.面片剔除
在面片的扩展过程中,可能会出现一些误差比较大的面片,因为需要剔除来确保面片的准确性。每次剔除分三步进行,每步的侧重不同,前两部从可视一致性入手,第三部强调面片间的关联性。
第一步,令U§表示与当前可视信息不连续的面片集合,所谓的不连续p和p’两个面片不属于邻近关系,但是却存在同一个Qi(x,y)中。对于U§中的面片p,如果满足下列条件,则将其过滤掉。

直观上来讲,如果p是一个异常值,那么1−g∗( p )和|V∗( p )|都会比较小,这样p一般都会被过滤掉。
第二步,对于每个面片p,我们计算它通过深度测试得到的可视图像的总数,如果数目小于r,则认为p是异常值,从而过滤掉。
第三步,对于每个面片p,在V( p )中,收集这样的一组面片,它们的映射到面片p自己所在的图像块以及所有相邻的图像块,如果p的八邻域内的面片数量占收集所得面片数量的比例小于0.25,则是异常值,将其过滤掉。

6.优缺点
优点:
朗伯面假设;容易产生空洞。
参考:https://blog.csdn.net/lhanchao/article/details/51885998
参考:https://cloud.tencent.com/developer/article/1903029

