matlab非线性规划的课后作业
前两天指导女朋友写了她们matlab课的课后作业，对于刚学这门课的同学们来说，感觉难度还行，废话不多说直接看题和放代码吧！
1、厂向用户提供发动机，合同规定，第一、二、三季度末分别交货40台、60台、80台．每季度的生产费用为 
（元），其中x是该季生产的台数．若交货后有剩余，可用于下季度交货，但需支付存储费，每台每季度c元．已知工厂每季度最大生产能力为100台，第一季度开始时无存货，设a=50、b=0.2、c=4，问工厂应如何安排生产计划，才能既满足合同又使总费用最低．讨论a、b、c变化对计划的影响，并作出合理的解释。
1.1建立模型
本题利用非线性规划(NonlinearProgramming)算法进行求解。
假设三个季度生产量分别为x1
、x2
、x3
。
再根据题目要求，可建立三者之间与收益量之间的方程式（式1）
建立方程式：
| f(x) = 54*x1+0.2*x1^1+50*x2+0.2*x2^2+54x3+0.2x3^2-160 |
(1) |
再列出x1
、x2
、x3
的取值范围：
| 40≤x1≤10060≤x2≤10080≤x3≤100 |
(2) |
接下来利用matlab自带fmincon函数：
| [x, fval] = fmincon(fun, x0, A, b, Aeq, beq, lb, ub, nonlcon) |
(3) |
1.2求出最优结果
将数据代入（3）式
计算出最优结果：
x1=40
、x2=62
、x3=100
代码如下：
主函数main：
%在a = 50、b = 0.2、c = 4的情况下求解既满足合同又使总费用最低的生产计划
%本题利用非线性规划(NonlinearProgramming)算法进行求解
%初始条件是x1 >=40、x2>=60、x3>=80
%设总花费主函数f(x)
%代入a、b、c得：f(x) = 54*x1+0.2*x1^1+50*x2+0.2*x2^2+54x3+0.2x3^2-160
fun = @(x)(54*x(1)+0.2*x(1)^1+50*x(2)+0.2*x(2)^2+54*x(3)+0.2*x(3)^2-160);%建立匿名函数
x0 = [0,0,0];% x0： 决策变量的初始值向量
% A,b,Aeq,beq,lb,ub同线性规划
A = [-1, 0 , 0; 60, -1, 0; 80, 80,-1];
b = [-40; 2400; 800];
Aeq = [];
beq = [];
lb = [40,60,80];
ub = [100,100,100];
[x, fval] = fmincon(fun, x0, A, b, Aeq, beq, lb, ub, @nonlcon)非线性约束函数句柄nonlcon：
% nonlcon：非线性约束函数的句柄
function [c, ceq] = nonlcon(x)
c = [1-x(1)*x(2); x(1)*x(2)-1.5];
ceq = x(1)^2+x(2)^2-3;
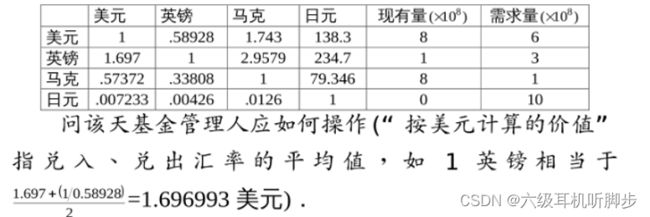
end2、一基金管理人的工作是﹐每天将现有的美元﹑英镑﹑马克﹑日元四种货币按当天汇率相互兑换﹐使在满足需要的条件下﹐按美元计算的价值最高·设某天的汇率﹑现有货币和当天需求如下:
1.1建立模型
本题利用非线性规划(NonlinearProgramming)算法进行求解。
兑换收益过程中首先要满足本货币的需求量，多出需求量的货币可通过货币兑换来获得增益，通过数学计算可假设兑换过程：
设x1:美元兑英镑的数量、x2:美元兑日元的数量、x3:马克兑英镑的数量、x4:马克兑日元的数量
讲题中所给数据设矩阵A和矩阵B：
A = [1,0.58928,1.743,138.3;
1.697,1,2.9579,234.7;
0.57372,0.33808,1,79.346;
0.007233,0.00426,0.0126,1]
B = [8,6;1,3;8,1;0,10];
通过A、B矩阵的运算，当日汇率为：
1英镑=1.696993美元、1日元=7.2318*10^-3美元、1英镑=2.9579马克、1日元=0.0126马克、1马克=0.573722美元。
假设三个季度生产量分别为x1、x2、x3。
再列出x1、x2、x3、x4的取值范围：
| 0≤x1≤20≤x2≤20≤x3≤70≤x4≤7 |
(1) |
接下来利用matlab自带fmincon函数：
| [x, fval] = fmincon(fun, x0, A, b, Aeq, beq, lb, ub, nonlcon) |
(2) |
1.2求出最优结果
将数据代入（5）式
计算出最优结果：
x1=1.1731、x2=1.2743、x3=2.362、x4=1.0554
代码如下：
主函数main2：
%货币兑换
A = [1,0.58928,1.743,138.3;
1.697,1,2.9579,234.7;
0.57372,0.33808,1,79.346;
0.007233,0.00426,0.0126,1];
B = [8,6; 1,3; 8,1;0,10];
%兑换收益过程中首先要满足本货币的需求量
%多出需求量的货币可通过货币兑换来获得增益
%通过数学计算可假设兑换过程：
%x1:美元兑英镑的数量
%x2:美元兑日元的数量
%x3:马克兑英镑的数量
%x4:马克兑日元的数量
%通过A矩阵的运算，当日汇率为：
%1英镑=1.696993美元、1日元=7.2318*10^-3美元、1英镑=2.9579马克、1日元=0.0126马克、1马克=0.573722美元
d= [ 1.696993,7.2318*10^-3,2.9579,0.0126];
d0 = 0.573722;
fun = @(x)(2-(d(1)*x(1)+d(2)*x(2))+d0*(7 - d(3)*x(3)-d(4)*x(4)));
% x0： 决策变量的初始值向量
x0 = [0,0,0,0];
% A,b,Aeq,beq,lb,ub同线性规划
A = [d(1),d(2),0,0;0,0,d(3),d(4)];
b = [2;7];
Aeq = [];
beq = [];
lb = [0,0,0,0];
ub = [2,2,7,7];
[x, fval] = fmincon(fun, x0, A, b, Aeq, beq, lb, ub, @nonlcon)非线性约束函数句柄nonlcon：
% nonlcon：非线性约束函数的句柄
function [c, ceq] = nonlcon(x)
c = [1-x(1)*x(2); x(1)*x(2)-1.5];
ceq = x(1)^2+x(2)^2-3;
end