dpfnet

论文阅读之：DPFNet: A Dual-branch Dilated Network with Phase-aware Fourier Convolution for Low-light Image Enhancement

代码：https://github.com/Zhuangyunliang/DPFNet

问题：

该领域常用的卷积神经网络擅长对空间域的低频局部结构特征进行采样，这导致了重建图像的纹理细节不明确。

解决：

1. 我们提出了一种利用傅里叶系数的新模块，该模块可以在频率相位的语义约束下恢复高质量的纹理细节，并补充空间域。

2. 我们设计了一个简单有效的图像空间域模块，利用不同接受域的扩张卷积，以减轻频繁降采样造成的细节损失。

我们将上述部分集成到一个端到端双分支网络中，设计了一个新的损失函数和一个自适应融合模块，引导网络灵活地结合空间域和频域特征，产生更好视觉效果。

创新：

• phase-aware Fourier convolution module（在图像傅里叶空间中重构在相位语义信息引导下的高频纹理细节，以补充空间域）
• 我们将空间域和频域增强集成到一个端到端双分支网络中。该网络能够集成低频和高频信息，同时捕获本地和全局交互。
• 我们提出一个傅里叶损失，以平衡空间和频域的特征，以恢复自然图像。

框架

方法

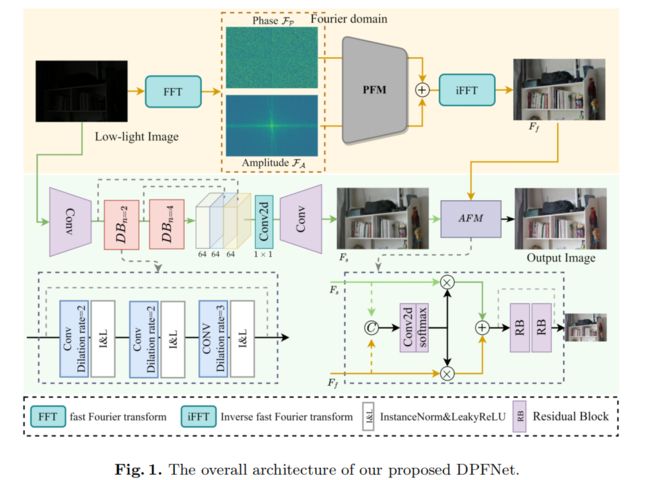
DPFNet主要由两个特征增强流和一个特征融合流组成。DPFNet的每个部分的设计：

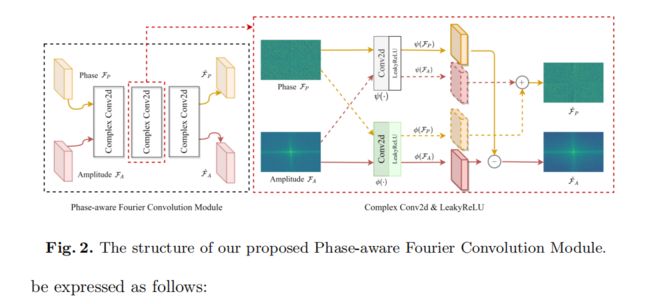
the phase-aware Fourier convolution module (PFM)

作用：在傅里叶域生成包含更多的全局和高频细节（上流），目的是在频域信息的辅助下恢复高频纹理细节，以补充空间域。

输入	输出	函数	作用	备注
$l_{low}$	fft的频域$\mathcal{F}(u,v)$【${\mathcal{F}}_{\mathcal{P}}$,${\mathcal{F}}_{\mathcal{A}}$】	$\mathcal{F}(u,v)={\sum }_{x,y}{I}_{low}(x,y)e^{-j2\pi \left(\frac{u}{M}x+\frac{v}{N}y\right)}$	任意频率的频谱包含了空间位置下的全局信息。	${\mathcal{F}}_{\mathcal{P}}$：（相位）语义结构 ${\mathcal{F}}_{\mathcal{A}}$：颜色纹理（振幅）
【${\mathcal{F}}_{\mathcal{P}}$,${\mathcal{F}}_{\mathcal{A}}$】	【${\mathcal{F}}_{\mathcal{P}}$,${\mathcal{F}}_{\mathcal{A}}$】	PFM（三个相同的复杂的结构）$\begin{array}{l}{\mathcal{F}}_P\leftarrow \varphi \left({\mathcal{F}}_P\right)+\psi \left({\mathcal{F}}_A\right)\\ {\mathcal{F}}_A\leftarrow \varphi \left({\mathcal{F}}_A\right)-\psi \left({\mathcal{F}}_P\right)\end{array}$	能增强阶段性语义指导，这是通过两种不同的实值卷积运算来实现的，其中实值卷积的滤波器的参数是共享的。	$\varphi (\cdot )\text{ and }\psi (\cdot )$是两个不想关的函数
【${\mathcal{F}}_{\mathcal{P}}$,${\mathcal{F}}_{\mathcal{A}}$】	${\mathcal{F}}_f$	$F_f=iFFT\left({\mathcal{F}}_A+j{\mathcal{F}}_P\right)$	将频率的增强频谱重构到空间域	其中j是复值虚部的单位

多层次扩张卷积（MDCM）

在空间域（底部流）中聚合了不同感受野下的局部上下文和内容特征。

$F_s=\varphi \left(\mathrm{cat}\left[D{B}_n\left(D{B}_{n-2}\left(F_{\text{local }}\right)\right),D{B}_{n-2}\left(F_{\text{local }}\right),F_{\text{local }}\right]\right)\oplus F_{\text{low }}$

式中，n表示DB中扩张卷积的膨胀率。受[14]的启发，我们在每个DB中添加了一个与膨胀率= n + 1的卷积，以缓解网格伪影。

自适应融合模块（AFM）

融合了空间域和频域特征，以避免过度增强的伪影，重建了更自然、高 质量的图像。有效地混合重建高质量的特性保持良好的可见性，我们拼接频率流的提取特征$F_f$和空间流的特征$F_s$通道维度。并且喂入一个卷积层去学习两个重要指标$w_f，w_s$，可以表示为：

$w_f,w_s=\mathrm{softmax}\left(\mathrm{Conv}\left(\mathrm{cat}\left[F_f,F_s\right]\right)\right)$

其中，Conv（·）为两个内核为3×3的卷积层。在重要性索引中，每个像素被分配一个对应的权值，该权重由对应的特征元素乘以每个元素来重构输出。恢复过程的定义如下：

$I_{norm}=R{B}_{\times 2}\left(F_f\otimes w_f\oplus F_s\otimes w_s\right)$

其中，⊗表示元素乘法，⊕表示元素加法。注意，输出通过两个残差块（RB）生成最终结果Inorm，以捕获图像增强的细微变化，使增强的图像看起来自然。

3.4 Loss Function

我们通过了一个损失组，由三个部分组成，每个部分都有特定的能力

SSIM Loss

由于低光图像的退化与许多不同的因素有关，使用$l_1$或$l_2$作为损失函数会导致不同程度的失真，并不能给出最理想的结果。相比之下，我们采用SSIM损失来整体评估亮度、对比度和结构等差异。具体来说，$l_s$被定义为${\mathcal{L}}_s=1-\mathrm{SSIM}\left(I_{norm},I_{gt}\right)$.其中，$I_{norm}$，$I_{gt}$表示增强的图像和地面真相，SSIM（·）表示SSIM [39]操作符.

Fourier Loss.

为了提高我们提出的模型对频率特征的敏感性，我们提出了一种基于频域空间的傅里叶损失（$L_f$）来指导模型重建高频细节。$L_f$可以看作是地面真实值与增强图像之间的频率距离的加权平均值，即为${\mathcal{L}}_f=\frac{1}{N}{\sum }_{i=0}^N{\Vert cat\left[I_{gt}^A,I_{gt}^P\right]-cat\left[I_{norm}^A,I_{norm}^P\right]\Vert }^2$,$I_{gt}^A,I_{gt}^P$通过FFT变换表示地面真实图像的振幅和相位分量，它们在通道维度上连接在一起，共同最小化地面真实图像与增强图像之间的间隙。

Perceptual Loss.

我们引入感知损失（$L_p$）[8]作为一种感知措施来利用图像的语义信息，提高增强图像的视觉质量。具体来说，我们使用欧氏距离来计算特征图之间的差值，公式定义如下：${\mathcal{L}}_p=\frac{1}{WHC}{\Vert \varphi \left(I_{gt}\right)-\varphi \left(I_{norm}\right)\Vert }^2$,其中，W、H、C分别表示图像的三维空间，预训练后的VGG网络[23]记为φ（·）。$L_p$平衡了$L_s$和$L_s$的指导作用，确保了我们的网络培训过程的稳定性。

Total Loss.

我们用损失组来构建总损失函数，即$\mathcal{L}={\mathcal{L}}_s+{\lambda }_a{\mathcal{L}}_f+{\lambda }_b{\mathcal{L}}_p$，其中，λa和λb是权衡权重超参数。大量的实验表明，当λa = 1.0和λb = 0.2时，我们的网络得到了最好的结果。

实验结果

al{L}_{p}$，其中，λa和λb是权衡权重超参数。大量的实验表明，当λa = 1.0和λb = 0.2时，我们的网络得到了最好的结果。

实验结果