关于谱图理论-图傅里叶变换-谱卷积等谱图领域知识的理解

前言

之前做可解释模型的时候，看了图卷积相关的资料及论文，对谱图理论及空域图理论有一些理解。这个博文包含了自己先前总结及思考的知识点，是一个 from scratch 的学习路线图。后续会逐步更新业界常见及最新的谱图及空域图相关论文。

重点需要理解的地方

• 傅立叶变换中的基的理解，即basis
• 图卷积的定义是为了迎合卷积定理?
• 图卷积 $f\ast h=U(U^{T}f\odot U^{T}h)$ 中的 $h$ 是卷积核，既可以作为顶点的函数，也可以作为特征向量的函数。

谱图理论(Spectral Graph Theory)

谱图理论是研究图的性质与特征多项式，特征值和与图相关的矩阵特征向量的关系，例如图的 邻接矩阵 和 Laplacian矩阵。¹

• Laplacian允许在离散表示（如graphs）和连续表示（如vector space和manifolds）之间建立自然链接。
• Laplacian最重要的应用是谱聚类(spectral clustering)，它对应于图的划分问题(graph partitioning problem)的计算上易于处理的解决方案。
• Laplacian另一个应用是谱匹配(spectral matching)，它解决了图匹配(graph matching)。

谱图理论应用：²

• 谱划分（Spectral partitioning）：Image Segmentation。我看了一些基于谱划分的paper，效果不是很好，远低于基于深度学习的paper。
• 文档分类、协同推荐等
• 流形分析（Manifold analysis）：流形嵌入（Manifold embedding）、流形学习（manifold learning）、网格分割（mesh segmentation）等。

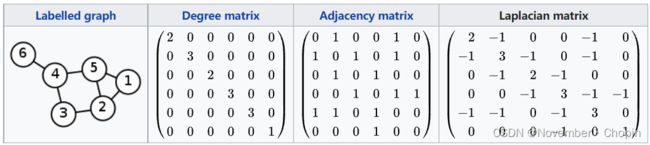
Laplacian矩阵

Laplacian矩阵简介

Laplacian矩阵是图的矩阵表示，可以看作是 有限差分法 得到的逼近负连续拉普拉斯的图上负离散拉普拉斯运算符的矩阵形式。 基于图的信号处理是基于 图傅里叶变换 ，它扩展了传统的 离散傅里叶变换 ，将 复正弦曲线的标准基 替换为对应于信号的 图拉普拉斯矩阵 的特征向量。³

Laplacian矩阵在 边加权图 的应用中更为常见，谱图理论 将图的属性与谱(spectrum)相关联，即与图相关的矩阵的特征值和特征向量，例如其邻接矩阵或Laplacian矩阵。不平衡的权重可能会对矩阵谱产生不利影响，导致需要归一化——矩阵条目(entries)的列/行缩放——导致归一化的邻接和Laplacian矩阵。

• 无向图Laplacian矩阵：$L=D-A$
  • $D$为度矩阵，$L$为邻接矩阵。在有向图中，度矩阵只需要考虑出度或者入度中的一个。
• 对称标准化Laplacian矩阵：$L^{sym}=(D^{+}{)}^{\frac{1}{2}}L(D^{+}{)}^{\frac{1}{2}}=I-(D^{+}{)}^{\frac{1}{2}}A(D^{+}{)}^{\frac{1}{2}}$
  • $D^{+}$是 穆尔-彭罗斯逆矩阵⁴，对称归一化Laplacian矩阵是对称的当且仅当邻接矩阵是对称的，也就是说图为无向图。 对于一个有向图的非对称邻接矩阵，可以使用出度和或入度中的任何一个进行规范化。
  • 对称标准化的Laplacian矩阵有一些优秀的性质，比如它的任何图的标准化拉普拉斯矩阵的征值范围在0到2之间，见博文《kipf-GCN中提到的标准化的拉普拉斯矩阵的性质》
• 左(随机游走)和右归一化Laplacians：$L^{rw}=D^{+}L=I-D^{+}A$
• 右归一化Laplacian矩阵：$L{D}^{+}=I-A{D}^{+}$

Laplacian矩阵特征分解

Laplacian矩阵分解(Laplacian Matrix Eigendecomposition)也称为谱分解(spectral decomposition)。
因为Laplacian矩阵是实对称矩阵，所以可以被正交对角化：
$$\begin{array}{r}L=U\Lambda U^T=U\left[\begin{array}{cccc}{\lambda }_1& & & \\ & {\lambda }_2& & \\ & & \ddots & \\ & & & {\lambda }_n\end{array}\right]U^T\end{array}$$
$U$是列向量为单位特征向量的矩阵，${\lambda }_l$为特征值。

从傅里叶变换到 图傅里叶变换

经典傅里叶变换

傅里叶级数知识参见：
\quad 矩形波的傅里叶级数及代码
FT参考链接：
\quad 傅里叶级数和傅里叶变换是什么关系？ - 马同学的回答 - 知乎
\quad 傅里叶系列（二）傅里叶变换的推导 - 知乎
\quad 傅里叶变换 – 从 Hilbert Space 到傅里叶变换基
\quad 傅里叶变换基的疑问

傅里叶级数是针对周期函数的，为了可以处理非周期函数，需要傅里叶变换(FT)。FT有助于将傅里叶级数扩展到非周期函数，这允许将任何函数视为简单正弦曲线的总和。

• FT将波形分解为正弦曲线，因此提供了另一种表示波形的方法。
• FT将作为时间函数的波形分解为构成它的频率。

传统的傅里叶变换公式为：
$$F(\omega )=\mathcal{F}[f(t)]={\int }_{-\infty }^{+\infty }f(t)e^{-i\omega t}dt$$

离散傅里叶变换及逆变换

参考wiki百科-Discrete Fourier transform
$$\begin{array}{rl}\mathcal{F}(k)=X_k& =\sum _{n=0}^{N-1}{x}_n\cdot e^{-\frac{i2\pi }{N}kn}\\ & =\sum _{n=0}^{N-1}{x}_n\cdot \left[\cos \left(\frac{2\pi }{N}kn\right)-i\cdot \sin \left(\frac{2\pi }{N}kn\right)\right],\end{array}$$

• 例子理解：
  令$N=4$，且$\mathbf{x}=\left(\begin{array}{c}{x}_0\\ x_1\\ x_2\\ x_3\end{array}\right)=\left(\begin{array}{c}1\\ 2-i\\ -i\\ -1+2i\end{array}\right)$，
  在这里，我们演示如何使用(2)式计算$\mathbf{x}$的DFT：
  $$\begin{array}{rl}\mathcal{F}(0)=X_0& =e^{-i2\pi 0\cdot 0/4}\cdot 1+e^{-i2\pi 0\cdot 1/4}\cdot (2-i)+e^{-i2\pi 0\cdot 2/4}\cdot (-i)+e^{-i2\pi 0\cdot 3/4}\cdot (-1+2i)=2\\ \mathcal{F}(1)=X_1& =e^{-i2\pi 1\cdot 0/4}\cdot 1+e^{-i2\pi 1\cdot 1/4}\cdot (2-i)+e^{-i2\pi 1\cdot 2/4}\cdot (-i)+e^{-i2\pi 1\cdot 3/4}\cdot (-1+2i)=-2-2i\\ \mathcal{F}(2)=X_2& =e^{-i2\pi 2\cdot 0/4}\cdot 1+e^{-i2\pi 2\cdot 1/4}\cdot (2-i)+e^{-i2\pi 2\cdot 2/4}\cdot (-i)+e^{-i2\pi 2\cdot 3/4}\cdot (-1+2i)=-2i\\ \mathcal{F}(3)=X_3& =e^{-i2\pi 3\cdot 0/4}\cdot 1+e^{-i2\pi 3\cdot 1/4}\cdot (2-i)+e^{-i2\pi 3\cdot 2/4}\cdot (-i)+e^{-i2\pi 3\cdot 3/4}\cdot (-1+2i)=4+4i\end{array}$$
  $$\mathbf{X}=\left(\begin{array}{c}{X}_0\\ X_1\\ X_2\\ X_3\end{array}\right)=\left(\begin{array}{c}2\\ -2-2i\\ -2i\\ 4+4i\end{array}\right)$$

图傅里叶变换及逆变换

本节的内容主要参考了Wiki百科-Graph Fourier Transform，并增加了一些便于理解的辅助知识。

这里的图傅里叶变换指的是"Graph Fourier Transform，GFT"，不是图像傅里叶变换（Image Fourier Transform）。同样，图傅里叶变换也有相应的逆变换——图傅里叶逆变换（Inverse Graph Fourier Transform，IGFT）

GFT

在数学中，图傅里叶变换是一种数学变换，它将图的Laplacian矩阵分解成特征值和特征向量。类似于经典傅立叶变换，$L$的特征值代表频率，特征向量形成所谓的图傅里叶基（DFT的基为$e^{-\frac{i2\pi }{N}kn}$）。

\quad	连续傅里叶变换	离散傅立叶变换	图傅立叶变换
变换基	$e^{-i2\pi ft}$	$e^{-\frac{i2\pi }{N}kn}$	$U^T$
维度	$\infty$	$N$(序列个数)	$N$(顶点个数)

对于无向带权图$G=(V,E)$，V是图结点(node)的集合，$|V|=N$是node的个数，$E$是边(edge)的集合。
图信号(graph signal) $f:V\to \mathbb{R}$ 是定义在图G顶点上的函数，$f$ 将每一个顶点(vertex⁵) $\{v_i{\}}_{i=1,\dots ,N}$ 映射为一个实数 $f(i)$ 。任何图信号都可以被映射在Laplacian矩阵 $L$ 的特征向量上。设 ${\lambda }_l$和${\mu }_l\in {\mathbb{R}}^{N\times 1}$ 为Laplacian矩阵 $L$ 的第 $l_{th}$ 个特征值和特征向量(特征值已经排序，$0={\lambda }_0\le {\lambda }_1\le \cdots \le {\lambda }_{N-1}$)，图信号 $f$ 在 $G$ 顶点上的图傅里叶变换$\hat{f}$ 是$f$在$L$的 本征函数 (eigenfunctions)⁶ 方面的扩展。定义为：
$$\begin{array}{r}\mathcal{GF}[f]({\lambda }_l)=\hat{f}\left({\lambda }_l\right)=⟨f,{\mu }_l⟩=\sum _{i=1}^{N}f(i){\mu }_l^{\ast }(i),\end{array}$$其中，${\mu }_l^{\ast }={\mu }_l^{\text{T}}$，${\mu }_l(i)$是$L$的第$l$个特征向量${\mu }_l$的第$i$个分量；$f(i)$图信号$f\in {\mathbb{R}}^{N\times 1}$的第$i$个分量，关于图信号$f$的通俗解释，参见博文。

将上述式子展开成矩阵的形式如下：
$$\left(\begin{array}{c}\hat{f}({\lambda }_1)\\ \hat{f}({\lambda }_2)\\ ⋮\\ \hat{f}({\lambda }_n)\end{array}\right)=\left[\begin{array}{cccc}{u}_1(1)& u_1(2)& \cdots & u_1(n)\\ u_2(1)& u_2(2)& \cdots & u_2(n)\\ ⋮& ⋮& & ⋮\\ u_n(1)& u_2(2)& \cdots & u_n(n)\end{array}\right]\cdot \left[\begin{array}{c}f(1)\\ f(2)\\ ⋮\\ f(n)\end{array}\right]$$所以GFT的向量形式为：
$$\begin{array}{r}\hat{f}=U^{T}f\end{array}$$ 其中， $U^T$ 的每一行是一个特征向量。

• 也有文献将其写作 $\hat{f}=U^{-1}f$，其实两者是等价的，因为拉普拉斯矩阵 $L$ 是实对称矩阵，其特征向量矩阵是正交矩阵，$U^{-1}=U^T$，可参考如下博文《拉普拉斯矩阵特征向量的几个关键性质证明》。

GFT 是变换 $U$ 在顶点函数 $f$ 上执行基的变化，将其表示为Laplacian特征函数的线性组合。根据上面的讨论，这可以被视为傅里叶变换的离散模拟。

IGFT

因为$L$是实对称矩阵，它的特征向量$\{{\mu }_l{\}}_{l=0,\cdots ,N-1}$形成正交基，因此存在图傅里叶逆变换：
$$\begin{array}{r}\mathcal{I}\mathcal{GF}[\hat{f}](i)=f(i)=\sum _{l=0}^{N-1}\hat{f}({\lambda }_l){\mu }_l(i)\end{array}$$ 所以IGFT的向量形式为：
$$\left[\begin{array}{c}f(1)\\ f(2)\\ ⋮\\ f(n)\end{array}\right]=\left[\begin{array}{cccc}{u}_1(1)& u_2(1)& \cdots & u_n(1)\\ u_1(2)& u_2(2)& \cdots & u_n(2)\\ ⋮& ⋮& & ⋮\\ u_1(n)& u_2(n)& \cdots & u_n(n)\end{array}\right]\cdot \left(\begin{array}{c}\hat{f}({\lambda }_1)\\ \hat{f}({\lambda }_2)\\ ⋮\\ \hat{f}({\lambda }_n)\end{array}\right)$$ 其中， $U$ 的每一列是一个特征向量。
IGFT的向量形式为：
$$\begin{array}{r}f=U\hat{f}\end{array}$$

GFT和IGFT小结

前两小节可以看到，图的傅里叶变换及其逆变换可以总结为：

对于 $L=U\Lambda U^T$，图的傅立叶变换及逆变换为$\{\begin{array}{l}GFT:\hat{f}=U^{T}f\\ IGFT:f=U\hat{f}\end{array}$

类似于经典的傅里叶变换，图傅里叶变换提供了一种在两个不同的域中表示信号的方法：顶点域(vertex domain)和谱域(spectral domain)。请注意，图傅里叶变换及其逆的定义取决于拉普拉斯特征向量的选择，它们不一定是唯一的。 归一化拉普拉斯矩阵的特征向量也是定义正向和反向图傅里叶变换的可能基础。

有文献将GFT和IGFT中 $U$ 的写法对调，即其写作$\{\begin{array}{l}\hat{f}=Uf\\ f=U^T\hat{f}\end{array}$，比如哈佛大学图书馆学术委员为办公室发布的讲义《Graph Convolutions and Machine Learning》,因为该文献的拉普拉斯矩阵相似对角化定义为 $L=U^T\Lambda U$。
此外，推荐使用 $L=U\Lambda U^T$表示，kipf-GCN就是使用这种表示方法。

举个GFT的例子理解

本小结已移入另一篇博客中，参见《图傅立叶变换的理解及例子》。

谱图卷积

在图神经网络，存在两种卷积，一个是谱图卷积（Spectral Graph Convolution），一个是空域图卷积。谱图卷积在早期就进入深入研究，直到kipf发表GCN引起Deep learning 界的广泛关注。空域卷积在GraphSage之后进入人们的视线。本节着重讲解谱图卷积。

卷积定理表明，两个函数（或信号）的卷积的傅里叶变换是它们傅里叶变换的逐点乘积。类似于离散时域/频域卷积定理，图的傅立叶变换也满足卷积定理。

传统卷积定义及卷积定理

本节请参阅我的两个博文，可以跟好地理解卷积：
卷积定义：《连续卷积和离散卷积定义及积分计算》
卷积定理：《时域卷积定理及频域卷积定理》

谱图卷积定义及谱卷积定理

• 谱卷积定义

定义：设两个定义在图上的函数 $f,h:V\to \mathbb{R}$ ，谱图卷积定义为：
$$\begin{array}{r}f\ast h=U(U^{T}f\odot U^{T}h)=U\left[\begin{array}{cccc}\hat{h}({\lambda }_1)& & & \\ & \hat{h}({\lambda }_2)& & \\ & & \ddots & \\ & & & \hat{h}({\lambda }_n)\end{array}\right]U^{T}f\end{array}$$ 其中，$\odot$ 表示点积：$(u\odot v{)}_i=u_i\cdot v_i$，$h$是卷积核。

(8)式等号后面的两种定义是等价的，证明请参考《GCN中的等式证明》。

• 谱卷积定理
  空间域$\Rightarrow$谱域：$\mathcal{GF}[f\ast g]=f\ast g=U^T\left(U\right(U^{T}f\odot U^{T}h\left)\right)=U^{T}f\odot U^{T}h=\hat{f}\odot \hat{h}$
  谱域$\Rightarrow$空间域：(目前还没有发现相关文献)

谱图卷积在深度学习中的应用

本节只简单介绍谱图卷积在深度学习中的使用，后续会有相关博文对第一代GCN、第二代GCN及kipf-GCN进行解读。

论文通常会将谱图卷积写成如下形式：
$$\begin{array}{r}{g}_{\theta }\star x=U{g}_{\theta }{U}^{T}x\end{array}$$ 其中，$x\in {\mathbb{R}}^N$ 是输入（每个顶点都是一个常数，一共 $N$ 个顶点）。$g_{\theta }=diag(\theta )$ 是卷积核($\theta \in {\mathbb{R}}^N$) ，且为 $L$ 特征值的函数，所以可以写为 $g_{\theta }(\Lambda )$。式(9)与式(8)是等价的。

最简单的情况，输入层为 $x$，则输出层为 $U{g}_{\theta }{U}^{T}x$，$\theta$ 是可训练参数。按照这种形式就可以一层一层堆叠。可以参考kipf的论文：《Semi-Supervised Classification With Graph Convolutional Networks》,ICLR,2017。

参考文献：

---

1. 维基百科-Spectral graph theory ↩︎

2. 图拉普拉斯、拉普拉斯嵌入和谱聚类的简短教程 ↩︎

3. 维基百科-Laplacian matrix ↩︎

4. 穆尔彭罗斯伪逆 ↩︎

5. 注意，vertex与node，关系紧密但略有不同，每一个vertex都将以node的形式在计算机中被表示和实现。参见链接 ↩︎

6. 维基百科-Eigenfunction ↩︎