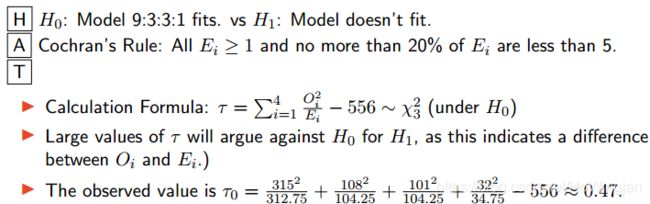统计基础（六）卡方分布
Test for Goodness of Fit
- 1.卡方分布
- 2.伽马分布
- 3.卡方独立性检验 Chi-square test for independence
- 4.卡方拟合优度检验 Chi-Square Goodness-of-Fit Test
- 5.孟德尔遗传案例
1.卡方分布
卡方分布是独立标准正态随机变量 Z i ∼ N ( 0 , 1 ) i = 1 , 2 ， … ， n Z_i \sim N(0,1) i = 1,2，…， n Zi∼N(0,1)i=1,2，…，n。它只能取正值，而且通常是右偏的。
我们说变量 X = ∑ i = 1 n Z i 2 ∼ X 2 X =\sum_{i=1}^n Z^2_i\sim X^2 X=∑i=1nZi2∼X2,有n个自由度，均值 E(X) = n，方差Var(X) = 2n。
概率分布函数pdf为
2.伽马分布
伽马分布 X ∼ Γ ( α , β ) X\sim\Gamma(\alpha,\beta) X∼Γ(α,β)
- α \alpha α形状参数（shape parameter)
决定了分布曲线的形状，也就是 α \alpha α不同，分布曲线形状不同 - β \beta β尺度参数（scale parameter）
在其他参数一定时， β \beta β不同，分布曲线的形状相似，但是高低、胖瘦不同，或者说是同一形状按照比例放大或缩小
概率密度分数
f ( x ) = 1 β α Γ ( α ) x α − 1 e − x β f(x)=\frac{1}{\beta^\alpha\Gamma(\alpha)}x^{\alpha-1}e^{\frac{-x}{\beta}} f(x)=βαΓ(α)1xα−1eβ−x其中， x > 0 , α > 0 , β > 0 x>0,\alpha>0,\beta>0 x>0,α>0,β>0
E ( X ) = α β E(X)=\alpha\beta E(X)=αβ 和 V a r ( X ) = α β 2 Var(X)=\alpha\beta^2 Var(X)=αβ2
卡方分布是伽马分布的一种特殊形式，其中 α = k / 2 , β = 2 , Γ ( α = k / 2 , β = 2 ) = X k 2 \alpha=k/2,\beta=2,\Gamma(\alpha=k/2,\beta=2)=X^2_k α=k/2,β=2,Γ(α=k/2,β=2)=Xk2
若 Q ∼ X k 2 , a Q ∼ Γ ( α = k / 2 , β = 2 Q\sim X^2_k, aQ \sim \Gamma(\alpha=k/2,\beta=2 Q∼Xk2,aQ∼Γ(α=k/2,β=2
3.卡方独立性检验 Chi-square test for independence
X^2测试是一个非常灵活的测试，因为它可以应用于一系列的情况。
- 离散概率与计数类别的拟合(孟德尔遗传学)
- 使用离散区间的连续数据拟合模型(随机数生成器)
我们将介绍最后一个例子，它着眼于如何建立两个离散变量之间的独立性。我们检验原假设H0:变量是独立的vs. HA:变量不是独立的。
判断行列是否独立
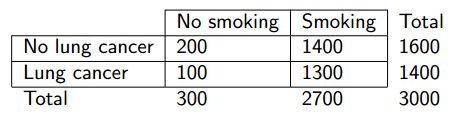
eg 检验是否吸烟与癌症之间的独立性
- 画出列联表
- 计算出列联表中的成分的概率
- 假设两个变量相互独立P(AB)=P(A)*P(B)
- 计算P值
4.卡方拟合优度检验 Chi-Square Goodness-of-Fit Test
考虑一组具有g类的分类数据，其中观察到的计数Oi，因为i = 1,2，…提出了一个类别的概率模型，我们想检验它是否与我们的预期值拟合。
5.孟德尔遗传案例
