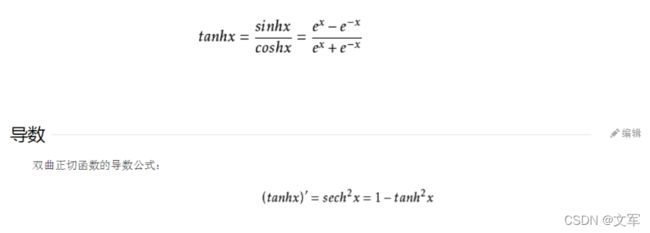感知机2-多层感知机
这意味着我们有1000个例子的28x28像素的灰度(即没有rgb通道)。
我们可以使用matplotlib来绘制其中的一些
这意味着我们有1000个例子的28x28像素的灰度(即没有rgb通道)。
我们可以使用matplotlib来绘制其中的一些
1.多层感知机(MLP)原理简介
多层感知机(MLP,Multilayer Perceptron)也叫人工神经网络(ANN,Artificial Neural Network),除了输入输出层,它中间可以有多个隐层,最简单的MLP只含一个隐层,即三层的结构,如下图:
![]()
从上图可以看到,多层感知机层与层之间是全连接的。多层感知机最底层是输入层,中间是隐藏层,最后是输出层。
隐藏层的神经元怎么得来?首先它与输入层是全连接的,假设输入层用向量X表示,则隐藏层的输出就是 f (W1X+b1),W1是权重(也叫连接系数),b1是偏置,函数f 可以是常用的sigmoid函数或者tanh函数:
注:神经网络中的Sigmoid型激活函数:
1. 为嘛使用激活函数?
a. 不使用激活函数,每一层输出都是上层输入的线性函数,无论神经网络有多少层,输出都是输入的线性组合。
b. 使用激活函数,能够给神经元引入非线性因素,使得神经网络可以任意逼近任何非线性函数,这样神经网络就可以利用到更多的非线性模型中。
激活函数需要具备以下几点性质:
1. 连续并可导(允许少数点上不可导)的非线性函数。可导的激活函数可以直接利用数值优化的方法来学习网络参数。
2. 激活函数及其导函数要尽可能的简单,有利于提高网络计算效率。
3. 激活函数的导函数的值域要在一个合适的区间内,不能太大也不能太小,否则会影响训练的效率和稳定性。
2. sigmod 函数
3 . Tanh 函数
取值范围为[-1,1]
tanh在特征相差明显时的效果会很好,在循环过程中会不断扩大特征效果。
与sigmod的区别是 tanh 是0 的均值,因此在实际应用中tanh会比sigmod更好。
在具体应用中,tanh函数相比于Sigmoid函数往往更具有优越性,这主要是因为Sigmoid函数在输入处于[-1,1]之间时,函数值变 化敏感,一旦接近或者超出区间就失去敏感性,处于饱和状态。
最后就是输出层,输出层与隐藏层是什么关系?
其实隐藏层到输出层可以看成是一个多类别的逻辑回归,也即softmax回归,所以输出层的输出就是softmax(W2X1+b2),X1表示隐藏层的输出f(W1X+b1)。
MLP整个模型就是这样子的,上面说的这个三层的MLP用公式总结起来就是,函数G是softmax。
因此,MLP所有的参数就是各个层之间的连接权重以及偏置,包括W1、b1、W2、b2。对于一个具体的问题,怎么确定这些参数?求解最佳的参数是一个最优化问题,解决最优化问题,最简单的就是梯度下降法了(SGD):首先随机初始化所有参数,然后迭代地训练,不断地计算梯度和更新参数,直到满足某个条件为止(比如误差足够小、迭代次数足够多时)。这个过程涉及到代价函数、规则化(Regularization)、学习速率(learning rate)、梯度计算等,
多层感知机的实现:
利用PyTorch设计神经网络拟合对Fashion-MNIST数据集进行分类。引入库
import torch
import torchvision
from torch.utils.data import DataLoader导入就绪后,我们可以继续准备将要使用的数据。但在那之前,我们将定义超参数,在这里,epoch的数量定义了我们将循环整个训练数据集的次数,而learning_rate和momentum是我们稍后将使用的优化器的超参数。
n_epochs = 3
batch_size_train = 64
batch_size_test = 1000
learning_rate = 0.01
momentum = 0.5
log_interval = 10
random_seed = 1
torch.manual_seed(random_seed)对于可重复的实验,我们必须为任何使用随机数产生的东西设置随机种子——如numpy和random!
现在我们还需要数据集的dataloader。这就是TorchVision发挥作用的地方。它让我们用一种方便的方式来加载MNIST数据集。我们将使用batch_size=64进行训练,并使用size=1000对这个数据集进行测试。下面的Normalize()转换使用的值0.1307和0.3081是MNIST数据集的全局平均值和标准偏差,这里我们将它们作为给定值。
TorchVision提供了许多方便的转换,比如裁剪或标准化。
train_loader = torch.utils.data.DataLoader(
torchvision.datasets.MNIST('./data/', train=True, download=True,
transform=torchvision.transforms.Compose([
torchvision.transforms.ToTensor(),
torchvision.transforms.Normalize(
(0.1307,), (0.3081,))
])),
batch_size=batch_size_train, shuffle=True)
test_loader = torch.utils.data.DataLoader(
torchvision.datasets.MNIST('./data/', train=False, download=True,
transform=torchvision.transforms.Compose([
torchvision.transforms.ToTensor(),
torchvision.transforms.Normalize(
(0.1307,), (0.3081,))
])),
batch_size=batch_size_test, shuffle=True)
运行上面的程序后,会自动将数据集下载到目录下的data文件夹。
除了数据集和批处理大小之外,PyTorch的DataLoader还包含一些有趣的选项。例如,我们可以使用num_workers > 1来使用子进程异步加载数据,或者使用固定RAM(通过pin_memory)来加速RAM到GPU的传输。但是因为这些在我们使用GPU时很重要,我们可以在这里省略它们。
现在让我们看一些例子。我们将为此使用test_loader。
让我们看看一批测试数据由什么组成。
examples = enumerate(test_loader)
batch_idx, (example_data, example_targets) = next(examples)
print(example_targets)
print(example_data.shape)import matplotlib.pyplot as plt
fig = plt.figure()
for i in range(6):
plt.subplot(2,3,i+1)
plt.tight_layout()
plt.imshow(example_data[i][0], cmap='gray', interpolation='none')
plt.title("Ground Truth: {}".format(example_targets[i]))
plt.xticks([])
plt.yticks([])
plt.show()这意味着我们有1000个例子的28x28像素的灰度(即没有rgb通道)。
我们可以使用matplotlib来绘制其中的一些
构建网络
现在让我们开始建立我们的网络。我们将使用两个2d卷积层,然后是两个全连接(或线性)层。作为激活函数,我们将选择整流线性单元(简称ReLUs),作为正则化的手段,我们将使用两个dropout层。在PyTorch中,构建网络的一个好方法是为我们希望构建的网络创建一个新类。让我们在这里导入一些子模块,以获得更具可读性的代码。
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.conv1 = nn.Conv2d(1, 10, kernel_size=5)
self.conv2 = nn.Conv2d(10, 20, kernel_size=5)
self.conv2_drop = nn.Dropout2d()
self.fc1 = nn.Linear(320, 50)
self.fc2 = nn.Linear(50, 10)
def forward(self, x):
x = F.relu(F.max_pool2d(self.conv1(x), 2))
x = F.relu(F.max_pool2d(self.conv2_drop(self.conv2(x)), 2))
x = x.view(-1, 320)
x = F.relu(self.fc1(x))
x = F.dropout(x, training=self.training)
x = self.fc2(x)
return F.log_softmax(x)
network = Net()
optimizer = optim.SGD(network.parameters(), lr=learning_rate,
momentum=momentum)
广义地说,我们可以想到torch.nn层中包含可训练的参数,而torch.nn.functional就是纯粹的功能性。forward()传递定义了使用给定的层和函数计算输出的方式。为了便于调试,在前向传递中打印出张量是完全可以的。在试验更复杂的模型时,这就派上用场了。请注意,前向传递可以使用成员变量甚至数据本身来确定执行路径——它还可以使用多个参数!
现在让我们初始化网络和优化器。
模型训练
是时候建立我们的训练循环了。首先,我们要确保我们的网络处于训练模式。然后,每个epoch对所有训练数据进行一次迭代。加载单独批次由DataLoader处理。
首先,我们需要使用optimizer.zero_grad()手动将梯度设置为零,因为PyTorch在默认情况下会累积梯度。然后,我们生成网络的输出(前向传递),并计算输出与真值标签之间的负对数概率损失。现在,我们收集一组新的梯度,并使用optimizer.step()将其传播回每个网络参数。有关PyTorch自动渐变系统内部工作方式的详细信息,请参阅autograd的官方文档(强烈推荐)。
我们还将使用一些打印输出来跟踪进度。为了在以后创建一个良好的培训曲线,我们还创建了两个列表来节省培训和测试损失。在x轴上,我们希望显示网络在培训期间看到的培训示例的数量。
train_losses = []
train_counter = []
test_losses = []
test_counter = [i*len(train_loader.dataset) for i in range(n_epochs + 1)]在开始训练之前,我们将运行一次测试循环,看看仅使用随机初始化的网络参数可以获得多大的精度/损失。你能猜出我们的准确度是多少吗?
def train(epoch):
network.train()
for batch_idx, (data, target) in enumerate(train_loader):
optimizer.zero_grad()
output = network(data)
loss = F.nll_loss(output, target)
loss.backward()
optimizer.step()
if batch_idx % log_interval == 0:
print('Train Epoch: {} [{}/{} ({:.0f}%)]\tLoss: {:.6f}'.format(
epoch, batch_idx * len(data), len(train_loader.dataset),
100. * batch_idx / len(train_loader), loss.item()))
train_losses.append(loss.item())
train_counter.append(
(batch_idx*64) + ((epoch-1)*len(train_loader.dataset)))
torch.save(network.state_dict(), './model.pth')
torch.save(optimizer.state_dict(), './optimizer.pth')
train(1)神经网络模块以及优化器能够使用.state_dict()保存和加载它们的内部状态。这样,如果需要,我们就可以继续从以前保存的状态dict中进行训练——只需调用.load_state_dict(state_dict)。
现在进入测试循环。在这里,我们总结了测试损失,并跟踪正确分类的数字来计算网络的精度。
def test():
network.eval()
test_loss = 0
correct = 0
with torch.no_grad():
for data, target in test_loader:
output = network(data)
test_loss += F.nll_loss(output, target, size_average=False).item()
pred = output.data.max(1, keepdim=True)[1]
correct += pred.eq(target.data.view_as(pred)).sum()
test_loss /= len(test_loader.dataset)
test_losses.append(test_loss)
print('\nTest set: Avg. loss: {:.4f}, Accuracy: {}/{} ({:.0f}%)\n'.format(
test_loss, correct, len(test_loader.dataset),
100. * correct / len(test_loader.dataset)))
test() 使用上下文管理器no_grad(),我们可以避免将生成网络输出的计算结果存储在计算图中。
是时候开始训练了!我们将在循环遍历n_epochs之前手动添加test()调用,以使用随机初始化的参数来评估我们的模型。
test()
for epoch in range(1, n_epochs + 1):
train(epoch)
test()参考:
(37条消息) 多层感知机(MLP)简介_北漂人家-CSDN博客_多层感知机
(37条消息) 用PyTorch实现MNIST手写数字识别(非常详细)_小锋学长生活大爆炸-CSDN博客_pytorch 手写数字识别