α-β剪枝算法学习寄（蒟蒻向，巨佬勿入）

 由于做某题时暴力分出来很低，但某巨佬告诉我α-β剪枝很好用于是本屑踏上了征途。作为一只屑屑在学习这个算法时到处看各种blog，于是乎被上界下界决策等一众本屑看不懂的词汇弄得晕头转向，这篇blog就用本屑的语言梳理一下α-β剪枝算法捏。

首先放一只定义：

Alpha-beta剪枝是一种搜索算法，用以减少极小化极大算法（Minimax算法）搜索树的节点数。这是一种对抗性搜索算法，主要应用于机器游玩的二人游戏（如井字棋、象棋、围棋）。当算法评估出某策略的后续走法比之前策略的还差时，就会停止计算该策略的后续发展。该算法和极suan所得结论相同，但剪去了不影响最终决定的分枝。

 简单点来说就是，双方轮流做选择，都想让自己得到最优结果，当一方发现自己做出某个决定后对方可能做出让自己的结果比当前最差结果更差的选择，这一方就会放弃这个选择。

貌似还是有点绕，举个栗子：

A，B两个特别聪明的人在van游戏，他们的面前有两组数，第一组中有一个3和一个5，第二组中有一个2和一个x，A希望得到尽可能大的数，B希望A得到尽可能小的数。A选择一组数，B选择一个数给A，由于B很聪明，他一定会选择较小的一个数给A，那么当A选择第一组，他可以得到3（当前最差结果）；当他选择第二组（另一选择），可以在x>2时得到2，在x<2时得到更小的某个数x（更差结果），显然这个时候A不需要知道x是多少，无论如何都不会选择牌组2（放弃选择）。

拓展一下，假设他们有了很多组数，每组有很多个数，这些组又组成了新的组，新的组也组成了组，以此类推，最后我们会发现它们可以组成一颗树，定义这棵树的节点表示当前选择A最后能得到的数。

那么在这里引入一些定义：

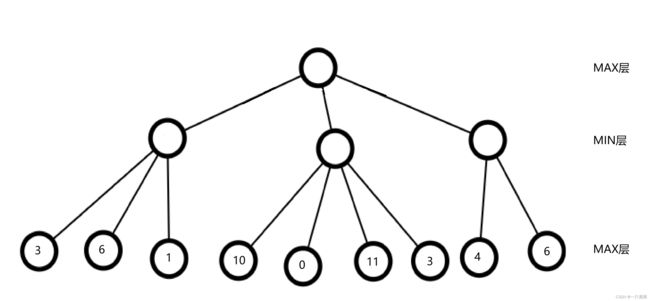
MAX层：MAX层中的节点会尽可能做使答案更优的选择，即A可能做选择的位置

MIN层：MAX层中的节点会尽可能做使答案更劣的选择，即B可能做选择的位置

MAX层与MIN层一定交替出现

如下图

 在α-β剪枝算法中，对于除叶子节点外的每个节点（因为叶子节点值固定）定义一个最小上界β表示选择该节点可能得到的最大值，一个最大下界α表示选择该节点可能得到的最小值；假设两个叶节点3,4在MIN层，他们的父节点在MAX层，那么父节点一定会选择一个大于等于4的值，故该节点的α为4；同理假设两个叶节点3,4在MAX层，他们的父节点在MIN层，那么父节点一定会选择一个小于等于3的值，故该节点的β为3。

那么可以得到：

对于MAX层，α=该节点所有子节点的最大值，β=其父节点的β

对于MIN层，α=其父节点的α，β=该节点所有子节点的最小值

当α>=β时放弃该节点（这个想不明白的可以重新看看前面的栗子捏）

想看具体模拟过程的小朋友可以看看Alpha-Beta 剪枝 - OI Wiki

代码就不挂了我自己题还没写出来（

最后用朴素minmax过了，不知道为什么加完α-β过不了（