R语言数据预处理方案

R语言数据挖掘与实战

一、数据探索

通过检验数据集的数据质量、绘制图表、计算某些特质量等手段，对样本数据集的结构和规律进行分析的过程就是数据探索。

1.1 数据质量分析

数据质量分析的主要任务是检查原始数据中是否存在脏数据，脏数据一般是指不符合要求，以及不能直接进行相应分析的数据，在常见的数据挖掘工作中，脏数据包括：

• 缺失值
• 异常值
• 不一致的值
• 重复数据及含有特殊符号（如#,￥、*）的数据。

1.1.1 缺失值分析

从统计上来说，缺失的数据可能会产生有偏估计，从而使得样本数据不能很好的代表总体，而现实中绝大部分数据都包含缺失值，因此，如何处理缺失值很重要。

一般来说，缺失值的处理包括两个步骤，即缺失数据的识别和缺失值处理。在R语言中缺失值通常以NA表示，可以使用函数is.na()判断缺失值是否存在，另外，函数complete.cases()可识别样本数据是否完整从而判断缺失情况。在对是否存在缺失值进行判断之后需要进行缺失值处理，常用的方法有删除法、替换法、插补法等。

（1）删除法

行删除：na.omit()

列删除：data[,-p]

（2）替换法

均值、中位数、众数来进行替换

（3）插补法

回归插补、多重插补

回归插补：利用回归模型，将需要插值补缺的变量作为因变量，其他相关变量作为自变量，通过回归函数lm()预测出因变量的值来对缺失变量进行补缺；

多重插补是从一个包含缺失值的数据集中生成一组完整的数据，如此进行多次，从而产生缺失值的一个随机样本，R中的mice函数包可以用来进行多重插补。

# 缺失值处理
inputfile<-read.csv("datas/catering_sale.csv",he=T)

# 变化变量名
inputfile = data.frame(sales=inputfile$销量,date=inputfile$日期)

# 数据截取
inputfile=inputfile[5:16,]

# 缺失数据识别
is.na(inputfile)
n<-sum(is.na(inputfile))


# 异常值识别
par(mfrow=c(1,2))  # 将窗口划分为1行两列，同时显示两个图
dotchart(inputfile$sales) #绘制单变量散点图
boxplot(inputfile$sales,horizontal = T)

# 异常值处理
inputfile$sales[5]=NA



# 缺失值的处理
inputfile$date=as.numeric(inputfile$date)  #将日期转换成数值型变量
sub<-which(is.na(inputfile$sales))
inputfile1<-inputfile[-sub,]
inputfile2<-inputfile[sub,]

# 行删除法处理缺失，结果转存
result1<-inputfile1
# 均值替换法处理缺失，结果转存
avg_sales = mean(inputfile1$sales)  # 求变量未缺失部分的均值
inputfile2$sales=rep(avg_sales,n)  # 用均值替换缺失

result2<-rbind(inputfile1,inputfile2)


# 回归插补法处理缺失，结果转存
model<-lm(sales~date,data = inputfile1)  #回归模型拟合
inputfile2$sales<-predict(model,inputfile2) #模型预测
result3<-rbind(inputfile1,inputfile2)

# 多重插补法处理缺失，结果转存
library(lattice)  #调入函数包
library(MASS)
library(nnet)
library(mice)
install.packages("mice")  #前三个包是mice的基础
imp<-mice(inputfile,m=4) # 4重插补，即生成4个无缺失数据集
fit=with(imp,lm(sales~date,data=inputfile))  # 选择插补模型
pooled=pool(fit)
summary(pooled)
result4<-complete(imp,action = 3)

# 在进行插值之前，会对数据进行异常值检测，发现数据为异常值，就定义为空缺值，进行补救

1.1.2 异常值处理

在异常值处理之前需要对异常值进行识别，一般采用单变量散点图或是箱型图来达到目的。在R中使用函数dotchart()、boxplot()实现绘制单变量散点图与箱型图。

异常值处理方法：

• 删除含有异常值的记录：直接将含有异常值的记录删除

• 视为缺失值：将异常值视为缺失值，利用缺失值处理的方法进行处理

• 平均值修正：可用前后两个观测值的平均值进行修正该异常值

• 不处理：直接在具有异常值的数据上进行挖掘建模

saledata<-read.csv("datas/catering_sale.csv",header = T)
# 缺失值检测并打印结果，由于R把TRUE和FALSE分别当做1/0,可以用sum()和mean()函数来分别获取缺失样本数、缺失比例。
sum(complete.cases(saledata))
sum(!complete.cases(saledata))
mean(!complete.cases(saledata))
saledata[!complete.cases(saledata),]

par(mfrow=c(1,1)) 
# 异常值检测箱型图
sp<-boxplot(saledata$销量,boxwex=0.7)
title("销量异常值检测箱型图")
xi=1.1
sd.s<-sd(saledata[complete.cases(saledata),]$销量)
mn.s<-mean(saledata[complete.cases(saledata),]$销量)
points(xi,mn.s,col='red',pch=8)
arrows(xi,mn.s-sd.s,xi,mn.s+sd.s,code = 3,col = "pink",angle = 75,length = .1)
text(rep(c(1.05,0.95),length(sp$out)/2),sp$out,sp$out,col = "red")

1.2 数据特征分析

1.2.1 分布分析

分布分析能揭示数据的分布特征和分布类型，对于定量数据，欲了解其分布形式是对称的还是非对称的、发现某些特大或特小的可疑值，可作出评率分布表、绘制频率分布直方图、绘制茎叶图进行直观的分析；对于定性数据，可以用饼形图和条形直观的现实分布情况。

（1）定量数据的分布分析

• 求极差
• 决定组距和组数
• 决定分点
• 列出频率分布表
• 绘制频率分布直方图

saledata <- read.table(file = "./data/catering_sale.csv", sep=",", header = TRUE) 
sales <- saledata[, 2]

# 统计量分析
# 均值
mean_ <- mean(sales, na.rm = T)
# 中位数
median_ <- median(sales, na.rm = T)
# 极差
range_ <- max(sales, na.rm = T) - min(sales, na.rm = T)
# 标准差
std_ <- sqrt(var(sales, na.rm = T))
# 变异系数
variation_ <- std_ / mean_
# 四分位数间距
q1 <- quantile(sales, 0.25, na.rm = T)
q3 <- quantile(sales, 0.75, na.rm = T)
distance <- q3 - q1
a <- matrix(c(mean_, median_, range_, std_, variation_, q1, q3, distance),
            1, byrow = T)
colnames(a) <- c("均值", "中位数", "极差", "标准差", "变异系数", 
                 "1/4分位数", "3/4分位数", "四分位间距")
print(a) 

1.2.2 统计量分析

用统计指标对定量数据进行统计描述，常从集中趋势和离中趋势两个方面进行分析。平均水平的指标是对个体集中趋势的度量，使用最广泛的是均值和中位数，反映变异程度的指标则是对个体离开平均水平的度量，使用较广泛的是标准差、方差、四分位间距。

（1）集中趋势度量

• 均值
• 中位数
• 众数

（2）离中趋势度量

• 极差
• 标准差
• 变异系数
• 四分位间距

1.2.3 周期性分析

周期性分析是探索某个变量是否随时间变化而呈现某种周期变化趋势。时间尺度相对较长的周期性趋势有年度周期性趋势、季节性周期性趋势，相对较短的有月度周期性趋势、周度周期性趋势、甚至更短的天。小时周期性趋势。

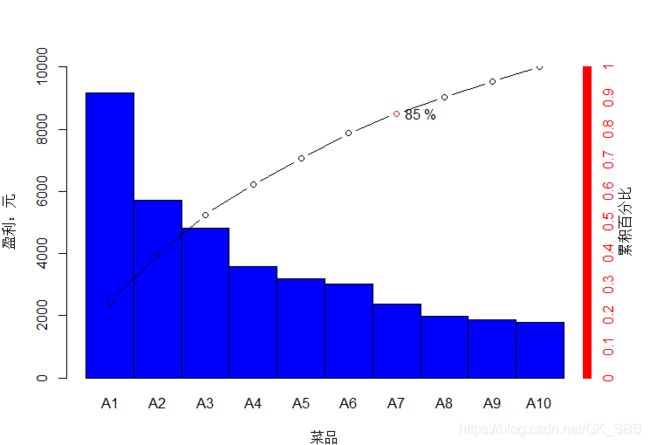
1.2.4 贡献度分析

贡献度分析又称为帕累托分析，它的原理是帕累托法则又称为20/80定律，同样的投入放在不同的地方会产生不同的效益。例如对一个公司来讲，80%的利润常常来自于20%最畅销的产品，而其他80%的产品只产生了20%的利润。

# 贡献度分析
# 读取菜品数据
dishdata<-read.csv("datas/catering_dish_profit.csv",header = T)

barplot(dishdata[,3],col = "blue1",names.arg = dishdata[,2],width = 1,space = 0,ylim = c(0,10000),xlab = "菜品",ylab="盈利：元")

accrato = dishdata[,3]
for (i in 1:length(accrato)) {
  accrato[i]=sum(dishdata[1:i,3])/sum(dishdata[,3])
  
}


par(new=T,mar=c(4,4,4,4))
points(accrato*10000~c((1:length(accrato)-0.5)),new=F,type='b',new=T)
axis(4,col="red",col.axis="red",at=0:10000,label=c(0:10000/10000))
mtext("累积百分比",4,2)
points(6.5,accrato[7]*10000,col='red')
text(7,accrato[7]*10000,paste(round(accrato[7]+0.00001,4)*100,"%"))

1.2.5 相关性分析

分析连续变量之间的线性相关程度，并用适当的统计指标表示出来的过程称为相关性分析。

（1）直接绘制散点图

判断两个变量是否具有线性的相关关系最直观的方法就是直接绘制散点图

（2）绘制散点图矩阵

需要同时考察多个变量间的相关关系时，一一绘制他们之间的简单散点图会十分麻烦，此时可利用散点图矩阵来同时绘制各个变量之间的散点图，从而快速发现多个变量之间的主要相关性，这在进行多元线性回归的时候显得尤为重要。

（3）计算相关系数

• Pearson相关系数
• Spearman秩相关系数
• 判定系数$R^2$

# 餐饮销量数据的相关性分析

cordata<-read.csv("datas/catering_sale_all.csv",header = T)
cordata<-na.omit(cordata)

res<-cor(cordata[,2:11])
library(corrplot)
corrplot(res, method = "shade",shade.col = NA, tl.col ="black", tl.srt = 45, order = "AOE") # 绘制相关系数矩阵图

#res：代表需要可视化的相关系数矩阵；

#method = "shade"代表指定可视化的方法，可以是圆形、方形、椭圆形、数值、阴影、颜色或饼图形，method = c("circle", "square", "ellipse", "number", "shade", "color", "pie")；

#shade.col = NA：指定图形展示的颜色，默认以均匀的颜色展示；

#tl.col：指定文本标签的颜色，即图形的文字标签是什么颜色的，默认为黑色；

#tl.srt = 45，表示文字标签的大小；

# order = "AOE"：指定相关系数排序的方法，可以是原始顺序(original)、特征向量角序(AOE)、第一主成分顺序(FPC)、层次聚类顺序(hclust)和字母顺序，一般”AOE”排序结果都比”FPC”要好，order = c("original", "AOE", "FPC", "hclust", "alphabet")。

1.3 数据变换

1.3.1 归一化

数据归一化处理是数据挖掘的一项基础工作，不同的评价指标往往有不同的量纲，数值间的差别可能很大，不进行处理可能会影响数据分析的结果，为了消除指标之间的量纲和取值范围差异的影响，需要进行标准化处理，将数据按照比例进行缩放，使之落入一个特定的区域，便于进行综合分析

• 最大-最小归一化
• 0均值归一化（均值为0 ，标准差为1）
• 小数定标规范化（通过移动属性值的小数位数，将属性值映射到[-1,1]）,移动的小数位数取决于属性值的最大值。

# 数据归一化
data_norm<-read.csv("datas/normalization_data.csv",he=F)
# 最大-最小归一化
b1<-(data_norm[,1]-min(data_norm[,1]))/(max(data_norm[,1])-min(data_norm[,1]))
b2<-(data_norm[,2]-min(data_norm[,2]))/(max(data_norm[,2])-min(data_norm[,2]))
b3<-(data_norm[,3]-min(data_norm[,3]))/(max(data_norm[,3])-min(data_norm[,3]))
b4<-(data_norm[,4]-min(data_norm[,4]))/(max(data_norm[,4])-min(data_norm[,4]))
data_scatter<-cbind(b1,b2,b3,b4)

data_scale<-scale(data_norm)
# 小数定标规范化
i1<-ceiling(log(max(abs(data_norm[,1])),10))
c1<-data_norm[,1]/10^i1

i2<-ceiling(log(max(abs(data_norm[,2])),10))
c2<-data_norm[,2]/10^i2

i3<-ceiling(log(max(abs(data_norm[,3])),10))
c3<-data_norm[,3]/10^i3

i4<-ceiling(log(max(abs(data_norm[,4])),10))
c4<-data_norm[,4]/10^i4

data_dot<-cbind(c1,c2,c3,c4)

# 打印结果
options(digits = 4)
data_norm
data_scatter
data_dot
data_scale

1.3.2 连续属性离散化

一些数据挖掘算法，特别是某些分类算法（如ID3算法，Aprior算法等），要求数据是分类属性形式。

（1）离散化的过程

连续属性的离散化就是在数据的取值范围内设定若干个离散的划分点，将取值范围划分为一些离散化的区间，最后用不同的符号或整数值代表落在子区间的数据值，所以，离散化涉及两个子任务：确定分类数以及如何将连续属性值映射到这些分类。

（2）常用的离散化方法

• 等宽法–该方法将属性的值域分成具有相同宽度的区间，区间的个数有数据本身的特点决定，或者有用户指定，类似于制作频率分布表
• 等频法–该法是将相同数量的记录放进每个区间
• （一维）聚类–包括两个步骤，首先将连续属性的值用聚类算法（K-means算法）进行聚类，然后将聚类得到的簇进行处理，合并到一个簇的连续属性值并做同一标记。