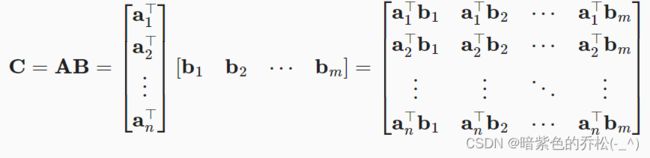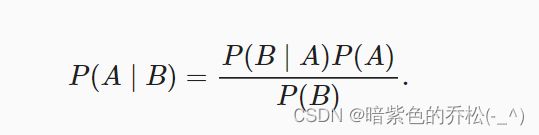深度学习——预备知识(3)线性代数、微积分、自动微分、概率、查阅文档
文章目录
- 2. 预备知识
-
- 2.3 线性代数
-
- 2.3.1性质、概念、基本操作
- 2.3.2 降维
- 2.3.2 非降维求和
- 2.3.3 点积
- 2.3.4 矩阵-向量积
- 2.3.5 矩阵-矩阵乘法
- 2.3.6 范数
- 总结
- 练习
- 2.4 微积分
- 2.5 自动微分
-
- 总结
- 2.6 概率
- 2.7 查阅文档
-
- 总结
2. 预备知识
2.3 线性代数
2.3.1性质、概念、基本操作
如果想说一个向量x由n个实值标量组成,可以表示成x属于R的n次幂(这里打字打不出来了)。
向量的长度称为向量的维度。
当用张量表示一个向量(只有一个轴)时,可以通过.shape属性访问向量的长度。
shape是一个元素组,列出了张量沿每个轴的长度(维数)。对于只有向量来说,元素组中只有一个元素。
概念区分:维度在不同场景下含义不同,向量或者轴的维度被用来表示向量或者轴的长度,就是向量或者轴的元素数量。但是,张量的维度用来表示张量具有的轴数。
张量的某个轴的维数就是这个轴的长度。
矩阵的表示:A属于R的(m乘n)次幂,表示m行,n列。
对称矩阵等于它的转置。
import torch
x=torch.tensor(3.0)
y=torch.tensor(2.0)
print(x+y)
print(x*y)
print(x/y)
print(x**y)
x=torch.arange(4)
print(x)
print(x[3])
#输出张量的长度
print(len(x))
print(x.shape)
#创建一个矩阵
A=torch.arange(20).reshape(5,4)
print(A)
# 访问矩阵的转置
print(A.T)
tensor(5.)
tensor(6.)
tensor(1.5000)
tensor(9.)
tensor([0, 1, 2, 3])
tensor(3)
4
torch.Size([4])
tensor([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11],
[12, 13, 14, 15],
[16, 17, 18, 19]])
tensor([[ 0, 4, 8, 12, 16],
[ 1, 5, 9, 13, 17],
[ 2, 6, 10, 14, 18],
[ 3, 7, 11, 15, 19]])
向量是一阶张量,矩阵是二阶张量,张量的范围更广。
# 三维张量
X=torch.arange(24).reshape(2,3,4);
print(X)
# 矩阵的加减
A=torch.arange(20,dtype=torch.float32).reshape(5,4)
B=A.clone()#通过分配新内存,将A的一个副本分配给B
print(A)
print(A+B)
print(A*B)
tensor([[[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]],
[[12, 13, 14, 15],
[16, 17, 18, 19],
[20, 21, 22, 23]]])
tensor([[ 0., 1., 2., 3.],
[ 4., 5., 6., 7.],
[ 8., 9., 10., 11.],
[12., 13., 14., 15.],
[16., 17., 18., 19.]])
tensor([[ 0., 2., 4., 6.],
[ 8., 10., 12., 14.],
[16., 18., 20., 22.],
[24., 26., 28., 30.],
[32., 34., 36., 38.]])
tensor([[ 0., 1., 4., 9.],
[ 16., 25., 36., 49.],
[ 64., 81., 100., 121.],
[144., 169., 196., 225.],
[256., 289., 324., 361.]])
两个矩阵按照元素乘法称为Hadamard积,数学符号为“⊙” 。运算过程如下图所示。
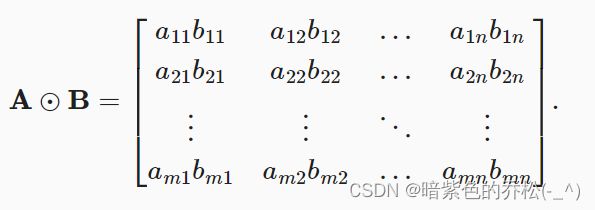
将张量乘以或者加上一个标量不会改变张量的形状,张量的每个元素都将与标量相加或者相乘。
a=2
X=torch.arange(24).reshape(2,3,4)
print(a+X)
print((a*X).shape)
tensor([[[ 2, 3, 4, 5],
[ 6, 7, 8, 9],
[10, 11, 12, 13]],
[[14, 15, 16, 17],
[18, 19, 20, 21],
[22, 23, 24, 25]]])
torch.Size([2, 3, 4])
2.3.2 降维
调用求和函数会沿所有的轴降低张量的维度,变为标量。可以指定张量沿哪一个轴来通过求和降低维度。
x=torch.arange(4,dtype=torch.float32)
print(x)
print(x.sum())
A_sum_axis0=A.sum(axis=0)
print(A)
print(A_sum_axis0)
print(A_sum_axis0.shape)
A_sum_axis1=A.sum(axis=1)
print(A_sum_axis1)
print(A_sum_axis1.shape)
tensor([0., 1., 2., 3.])
tensor(6.)
tensor([[ 0., 1., 2., 3.],
[ 4., 5., 6., 7.],
[ 8., 9., 10., 11.],
[12., 13., 14., 15.],
[16., 17., 18., 19.]])
tensor([40., 45., 50., 55.])
torch.Size([4])
tensor([ 6., 22., 38., 54., 70.])
torch.Size([5])
沿着行和列对矩阵求和,等价于对矩阵的所有元素进行求和。
print(A.sum(axis=[0,1]))
tensor(190.)
与求和相关的量是平均值(mean或者average)。通过将总和除以元素总数来计算平均值。
print(A.mean())
print(A.sum()/A.numel())
tensor(9.5000)
tensor(9.5000)
计算平均值的函数也可以沿指定轴降低张量的维度。
print(A)
print(A.mean(axis=0))
print(A.sum(axis=0)/A.shape[0])
tensor([[ 0., 1., 2., 3.],
[ 4., 5., 6., 7.],
[ 8., 9., 10., 11.],
[12., 13., 14., 15.],
[16., 17., 18., 19.]])
tensor([ 8., 9., 10., 11.])
tensor([ 8., 9., 10., 11.])
2.3.2 非降维求和
在调用函数总和或者均值可以保持轴数不变
sum_A=A.sum(axis=1,keepdims=True)
print(sum_A)
tensor([[ 6.],
[22.],
[38.],
[54.],
[70.]])
由于sum_A在对每行进行求和后仍然保持两个轴,可以通过广播将A除以sum_A。
print(A/sum_A)
tensor([[0.0000, 0.1667, 0.3333, 0.5000],
[0.1818, 0.2273, 0.2727, 0.3182],
[0.2105, 0.2368, 0.2632, 0.2895],
[0.2222, 0.2407, 0.2593, 0.2778],
[0.2286, 0.2429, 0.2571, 0.2714]])
沿某个轴计算累积总和
print(A)
print(A.cumsum(axis=0))
tensor([[ 0., 1., 2., 3.],
[ 4., 5., 6., 7.],
[ 8., 9., 10., 11.],
[12., 13., 14., 15.],
[16., 17., 18., 19.]])
tensor([[ 0., 1., 2., 3.],
[ 4., 6., 8., 10.],
[12., 15., 18., 21.],
[24., 28., 32., 36.],
[40., 45., 50., 55.]])
2.3.3 点积
点积是按相同位置的按元素乘积的和。
x=torch.arange(4.0)
y=torch.ones(4,dtype=torch.float32)
print(x)
print(y)
print(torch.dot(x, y))
tensor([0., 1., 2., 3.])
tensor([1., 1., 1., 1.])
tensor(6.)
或者通过执行元素乘法,然后进行求和来表示两个向量的点积。
print(torch.sum(x*y))
tensor(6.)
将两个向量规范化得到单位长度后,点积表示夹角的余弦。
2.3.4 矩阵-向量积
矩阵可以用行向量表示。

矩阵向量积AX是一个长度为m的列向量。

使用mv函数来计算矩阵-向量积,注意A的列维数(沿轴1的方向)必须与x的维数(其长度)相同。
print(A)
print(A.shape)
print(x)
print(x.shape)
print(torch.mv(A,x))
tensor([[ 0., 1., 2., 3.],
[ 4., 5., 6., 7.],
[ 8., 9., 10., 11.],
[12., 13., 14., 15.],
[16., 17., 18., 19.]])
torch.Size([5, 4])
tensor([0., 1., 2., 3.])
torch.Size([4])
tensor([ 14., 38., 62., 86., 110.])
2.3.5 矩阵-矩阵乘法
由第一个矩阵的行乘以第二个矩阵的列,求出结果即可。
假设有两个矩阵:

变成A的行向量和B的列向量:

print(A)
B=torch.ones(4,3)
print(B)
print(torch.mm(A,B))
tensor([[ 0., 1., 2., 3.],
[ 4., 5., 6., 7.],
[ 8., 9., 10., 11.],
[12., 13., 14., 15.],
[16., 17., 18., 19.]])
tensor([[1., 1., 1.],
[1., 1., 1.],
[1., 1., 1.],
[1., 1., 1.]])
tensor([[ 6., 6., 6.],
[22., 22., 22.],
[38., 38., 38.],
[54., 54., 54.],
[70., 70., 70.]])
2.3.6 范数
线性代数中最有用的一些运算符是范数。向量的范数是表示一个向量有多大,这个大小不涉及维度,而是分量的大小。
在线性代数中,向量范数是将向量映射到标量的函数。给定任意向量,向量范数要满足一些属性。第一个性质是:如果我们按常数因子缩放向量的所有元素,其范数也会按相同常数因子的绝对值缩放:

第二个是三角不等式:

u = torch.tensor([3.0, -4.0])
print(u)
print(torch.norm(u))
tensor([ 3., -4.])
tensor(5.)
print(torch.abs(u).sum())
tensor(7.)
L1范数受异常值的影响较小。
L2范数和L1范数都是更一般的Lp范数的特例,Lp范数:

Frobenius范数,矩阵元素平方和的平方根:
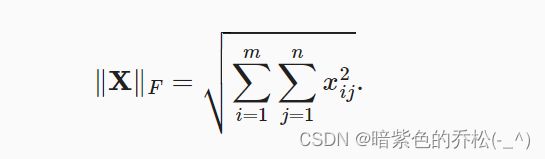
print(torch.ones(4,9))
print(torch.norm(torch.ones(4,9)))
tensor([[1., 1., 1., 1., 1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1., 1., 1., 1., 1.]])
tensor(6.)
总结
- 标量、向量、矩阵和张量是线性代数的基本数学对象。
- 标量、向量、矩阵和张量分别具有0,1,2和任意数量的轴。
- 一个张量可以通过sum和mean沿指定的轴降低维度。
- 两个矩阵的按元素乘法被称为他们的Hadamard积,与矩阵乘法不同。
- 在深度学习中,会经常使用范数,如L1范数,L2范数和Frobenius范数。
练习
- 定义形状(2,3,4)张量X,len(X)的输出结果是什么?
T=torch.arange(24).reshape(2,3,4)
print(T)
tensor([[[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]],
[[12, 13, 14, 15],
[16, 17, 18, 19],
[20, 21, 22, 23]]])
2.对于任意形状的张量X, len(X)是否总是对应于X特定轴的长度?这个轴是什么?
总是对应axis=0这个轴。
T=torch.arange(24).reshape(2,3,4)
print(T)
print(len(T))
T=torch.arange(24).reshape(3,8)
print(T)
print(len(T))
tensor([[[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]],
[[12, 13, 14, 15],
[16, 17, 18, 19],
[20, 21, 22, 23]]])
2
tensor([[ 0, 1, 2, 3, 4, 5, 6, 7],
[ 8, 9, 10, 11, 12, 13, 14, 15],
[16, 17, 18, 19, 20, 21, 22, 23]])
3
Process finished with exit code 0
3.运行A/A.sum(axis=1),会发生什么。分析一下原因?
这句话是说,要对矩阵进行归一化,使得每行的和为1,但是这样写会报错,要加上keepdims=True就可以了,是因为广播机制的原因。axis=0时不需要加keepdims。
print(A/A.sum(axis=1,keepdim=True))可以理解为在(5,4)和(5,1)之间广播,这是合法的。
可以这样理解,一个向量总是默认将其作为行向量,当广播时,对齐操作对象间的shape时,默认会右对齐,所以(5,4)和(5)进行右对齐后维数不匹配,所以广播失败。但是(5,4)和(4)之间可以广播。
A=torch.arange(20,dtype=torch.float32).reshape(5,4)
print(A)
# 这样写会报错,是因为广播机制,在axis不等于0时一般需要加上keepdim=True
# print(A/A.sum(axis=1))
print(A.sum(axis=1))
print(A/A.sum(axis=1,keepdim=True))
tensor([[ 0., 1., 2., 3.],
[ 4., 5., 6., 7.],
[ 8., 9., 10., 11.],
[12., 13., 14., 15.],
[16., 17., 18., 19.]])
tensor([ 6., 22., 38., 54., 70.])
tensor([[0.0000, 0.1667, 0.3333, 0.5000],
[0.1818, 0.2273, 0.2727, 0.3182],
[0.2105, 0.2368, 0.2632, 0.2895],
[0.2222, 0.2407, 0.2593, 0.2778],
[0.2286, 0.2429, 0.2571, 0.2714]])
Process finished with exit code 0
4.考虑一个具有形状的张量,在轴0、1、2上的求和输出是什么形状?
T=torch.arange(24).reshape(2,3,4)
sum1=T.sum(axis=0,keepdims=True)
sum2=T.sum(axis=1,keepdims=True)
sum3=T.sum(axis=2,keepdims=True)
print("T的形状:")
print(T)
print(T.shape)
print("在轴0求和输出:")
print(sum1)
print(sum1.shape)
print("在轴1求和输出:")
print(sum2)
print(sum2.shape)
print("在轴2求和输出:")
print(sum3)
print(sum3.shape)
T的形状:
tensor([[[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]],
[[12, 13, 14, 15],
[16, 17, 18, 19],
[20, 21, 22, 23]]])
torch.Size([2, 3, 4])
在轴0求和输出:
tensor([[[12, 14, 16, 18],
[20, 22, 24, 26],
[28, 30, 32, 34]]])
torch.Size([1, 3, 4])
在轴1求和输出:
tensor([[[12, 15, 18, 21]],
[[48, 51, 54, 57]]])
torch.Size([2, 1, 4])
在轴2求和输出:
tensor([[[ 6],
[22],
[38]],
[[54],
[70],
[86]]])
torch.Size([2, 3, 1])
2.4 微积分
两个概念
优化:用模型拟合观测数据的过程。
泛化:数学原理和实践者的智慧,能够知道我们生成出有效超出用于训练的数据集本身的模型。
梯度:连接一个多元函数对其所有变量的偏导数,以得到该函数的梯度向量。假设x是一个n维向量,函数f(x)相对于x的梯度是一个包含n个偏导数的向量:(下图中倒三角形右边的那个小无歧义时可以省略)

2.5 自动微分
import torch
x=torch.arange(4.0)
print(x)
x=torch.arange(4.0,requires_grad=True)
# 默认值是None
print(x.grad)
y=2*torch.dot(x,x)
print(y)
#调用反向传播函数来自动计算y关于x每个分量的梯度,打印梯度
y.backward()
print(x.grad)
tensor([0., 1., 2., 3.])
None
tensor(28., grad_fn=<MulBackward0>)
tensor([ 0., 4., 8., 12.])
总结
深度学习框架可以自动计算导数,首先将梯度附加到想要对其计算偏导数的变量上,然后记录目标值的计算,执行它的反向传播函数,并访问得到的梯度。
2.6 概率
2.7 查阅文档
查找模块中的所有函数和类——dir。通常忽略以双下划线开始和结束的函数,往往是特殊对象,或者以单下划线开始的函数,它们通常是内部函数。
import torch
print(dir(torch.distributions))
['AbsTransform', 'AffineTransform', 'Bernoulli', 'Beta', 'Binomial', 'CatTransform', 'Categorical', 'Cauchy', 'Chi2', 'ComposeTransform', 'ContinuousBernoulli', 'CorrCholeskyTransform', 'Dirichlet', 'Distribution', 'ExpTransform', 'Exponential', 'ExponentialFamily', 'FisherSnedecor', 'Gamma', 'Geometric', 'Gumbel', 'HalfCauchy', 'HalfNormal', 'Independent', 'IndependentTransform', 'Kumaraswamy', 'LKJCholesky', 'Laplace', 'LogNormal', 'LogisticNormal', 'LowRankMultivariateNormal', 'LowerCholeskyTransform', 'MixtureSameFamily', 'Multinomial', 'MultivariateNormal', 'NegativeBinomial', 'Normal', 'OneHotCategorical', 'OneHotCategoricalStraightThrough', 'Pareto', 'Poisson', 'PowerTransform', 'RelaxedBernoulli', 'RelaxedOneHotCategorical', 'ReshapeTransform', 'SigmoidTransform', 'SoftmaxTransform', 'StackTransform', 'StickBreakingTransform', 'StudentT', 'TanhTransform', 'Transform', 'TransformedDistribution', 'Uniform', 'VonMises', 'Weibull', '__all__', '__builtins__', '__cached__', '__doc__', '__file__', '__loader__', '__name__', '__package__', '__path__', '__spec__', 'bernoulli', 'beta', 'biject_to', 'binomial', 'categorical', 'cauchy', 'chi2', 'constraint_registry', 'constraints', 'continuous_bernoulli', 'dirichlet', 'distribution', 'exp_family', 'exponential', 'fishersnedecor', 'gamma', 'geometric', 'gumbel', 'half_cauchy', 'half_normal', 'identity_transform', 'independent', 'kl', 'kl_divergence', 'kumaraswamy', 'laplace', 'lkj_cholesky', 'log_normal', 'logistic_normal', 'lowrank_multivariate_normal', 'mixture_same_family', 'multinomial', 'multivariate_normal', 'negative_binomial', 'normal', 'one_hot_categorical', 'pareto', 'poisson', 'register_kl', 'relaxed_bernoulli', 'relaxed_categorical', 'studentT', 'transform_to', 'transformed_distribution', 'transforms', 'uniform', 'utils', 'von_mises', 'weibull']
查找特定函数和类的用法——help。例如查看张量ones函数的用法。
help(torch.ones)
总结
一些用法可以查看官方文档。
在Jupyter记事本中,可以使用?指令在另一个浏览器窗口中显示文档。例如,list?指令将创建与help(list)指令几乎相同的内容,并在新的浏览器窗口中显示它。如果使用两个问号,例如list??,将显示函数的python代码。