使用MATLAB实现基于小波变换的信号去噪
使用MATLAB实现基于小波变换的信号去噪
- 前言
- 一、需要调用的子函数
-
- 1、Gnoisegen函数
- 2、levelandth1函数
- 3、level函数
- 4、snrr函数
- 二、生成原始信号和加噪信号
- 三、探讨小波基对去噪效果的影响
- 四、探讨分解层数对去噪效果的影响
- 五、改进阈值函数
- 六、各阈值函数、阈值估计方法的去噪效果
-
- 1、生成去噪效果图
- 2、计算去噪后信噪比
- 参考文献
前言
本文中代码主要完成以下工作:
1、探讨小波基、分解层数、阈值估计方法、阈值函数的选择对去噪效果的影响。
2、对阈值函数进行改进,并利用改进算法进行去噪,验证其有效性。
(以信噪比作为评价去噪性能的指标)
PS:参考了当码网上大佬的代码,进行修改后运行通过,若有错误烦请指正。
一、需要调用的子函数
1、Gnoisegen函数
在原始信号上加高斯白噪声,信噪比通过snr设置。
function [y,noise] = Gnoisegen(x,snr) %x是原始信号,y是加噪信号
noise=randn(size(x));
Nx=length(x);
signal_power=1/Nx*sum(x.*x);
noise_power=1/Nx*sum(noise.*noise);
noise_variance=signal_power/(10^(snr/10));
noise=sqrt(noise_variance/noise_power)*noise;
y=x+noise;
2、levelandth1函数
计算同一小波系下各阶小波基去噪后的信噪比。
function snrwave=levelandth1(y,s,wave,n)%wave为选定的小波系
for j=1:n %依次选择同一小波系下的各阶小波基
xdh=wden(s,'sqtwolog','s','mln',5,wave(j,:));
snrwave(j)=snrr(y,xdh);
end
end
3、level函数
计算分解层数依次为1~10去噪后的信噪比。
function [z,snrxd]=level(y,s,th,wave)%s为加噪信号
for k=1:10 %依次选择分解层数
xdh=wden(s,th,'s','mln',k,wave);
snrxd(k)=snrr(y,xdh);
end
[~,z]=max(snrxd);
end
4、snrr函数
计算去噪后信噪比,以评价去噪性能。
S N R = 10 l g 1 L ∑ n = 1 L x 2 ( n ) 1 L ∑ n = 1 L [ x ( n ) − y ( n ) ] 2 \ SNR = 10lg\frac{\frac{1}{L}\sum_{n=1}^Lx^2(n)}{\frac{1}{L}\sum_{n=1}^L[x(n)-y(n)]^2} SNR=10lgL1∑n=1L[x(n)−y(n)]2L1∑n=1Lx2(n)
式中, x ( n ) x(n) x(n)为原始信号, y ( n ) y(n) y(n)为去噪后信号, L L L为信号总采样点数。
function z=snrr(x,y)%x是原始信号,y是去噪后信号
y1=sum(x.^2);
y2=sum((y-x).^2);
z=10*log10((y1/y2));
end
二、生成原始信号和加噪信号
原始信号和噪声信号可根据需要自己设置,这里我们生成一个正弦信号,并加以高斯白噪声。
clear all;
clc;
close all;
snr=5;%设置信噪比
N=1000;
t=1:N;
y=sin(0.03*t);%生成正弦信号
[s,noise]=Gnoisegen(y,snr);%加高斯白噪声
figure(1)
subplot(211);
plot(y);
xlabel('样本序号');
ylabel('幅值');
title('原始信号');
subplot(212);
plot(s);
xlabel('样本序号');
ylabel('幅值');
title('加噪信号');
三、探讨小波基对去噪效果的影响
生成同一小波系下各阶小波基与去噪后信噪比的关系曲线图。
sym=['sym1';'sym2';'sym3';'sym4';'sym5';'sym6';'sym7';'sym8'];
db=['db1';'db2';'db3';'db4';'db5';'db6';'db7';'db8'];
coif=['coif1';'coif2';'coif3';'coif4';'coif5'];
snrsym=levelandth1(y,s,sym,8);
snrdb=levelandth1(y,s,db,8);
snrcoif=levelandth1(y,s,coif,5);
ksym=1:8;
kdb=1:8;
kcoif=1:5;
figure(2)
plot(ksym,snrsym,'r-',kdb,snrdb,'g-',kcoif,snrcoif,'b-'),grid on;
legend('sym小波系','db小波系','coif小波系');
xlabel('小波基');
ylabel(' 去噪后信噪比/dB');
title('小波基和去噪后信噪比的关系');
四、探讨分解层数对去噪效果的影响
生成分解层数与去噪后信噪比的关系曲线图,并输出各阈值估计方法下的最佳分解层数。
thrrr1='sqtwolog';
thrrr2='rigrsure';
thrrr3='heursure';
thrrr4='minimaxi';
wavec='sym4';
[M1,snrxd1]=level(y,s,thrrr1,wavec);%确定最佳分解层数
[M2,snrxd2]=level(y,s,thrrr2,wavec);
[M3,snrxd3]=level(y,s,thrrr3,wavec);
[M4,snrxd4]=level(y,s,thrrr4,wavec);
fprintf('sqtwolog阈值最佳分解层数:%d \n',M1);
fprintf('rigrsure阈值最佳分解层数: %d\n',M2);
fprintf('heursure阈值最佳分解层数: %d\n',M3);
fprintf('minimaxi阈值最佳分解层数: %d\n',M4);
k=1:10;
figure(3)
plot(k,snrxd1,'r-',k,snrxd2,'m-',k,snrxd3,'g-',k,snrxd4,'b-'),grid on;
legend('sqtwolog阈值','rigrsure阈值','heursure阈值','minimaxi阈值');
xlabel('分解层数');
ylabel(' 去噪后信噪比/dB');
title('分解层数和去噪后信噪比的关系');
五、改进阈值函数
d ^ j , k = { d j , k − λ 1 + e ( d j , k − λ ) 2 a − λ 2 e 1 a , d j , k ⩾ λ 0 , ∣ d j , k ∣ < λ d j , k + λ 1 + e ( − d j , k − λ ) 2 a + λ 2 e 1 a , d j , k ⩽ − λ \hat d_{j,k}= \begin{cases} \\d_{j,k}-\frac{\lambda}{1+e^{\frac{(d_{j,k}-\lambda)^2}{a}}}-\frac{\lambda}{2e^{\frac{1}{a}}}, & \text{$d_{j,k}\geqslant\lambda$} \\[2ex] 0, & \text{$|d_{j,k}|\lt\lambda$} \\[2ex] \\d_{j,k}+\frac{\lambda}{1+e^{\frac{(-d_{j,k}-\lambda)^2}{a}}}+\frac{\lambda}{2e^{\frac{1}{a}}}, & \text{$d_{j,k}\leqslant-\lambda$} \end{cases} d^j,k=⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧dj,k−1+ea(dj,k−λ)2λ−2ea1λ,0,dj,k+1+ea(−dj,k−λ)2λ+2ea1λ,dj,k⩾λ∣dj,k∣<λdj,k⩽−λ
式中, d j , k d_{j,k} dj,k为加噪语音信号的小波系数, d ^ j , k \hat d_{j,k} d^j,k为加噪语音信号去噪处理后的小波系数, λ \lambda λ为阈值, a a a为调节因子,取值范围为 [ 0 , + ∞ ) [0,+\infty) [0,+∞)。
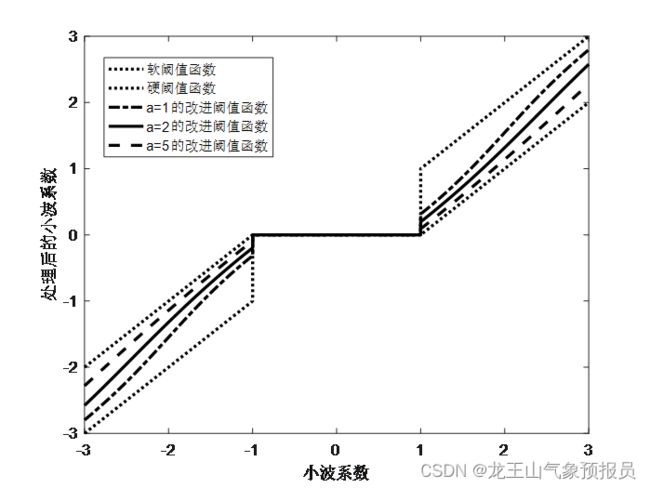
调节a的值可以得到不同的阈值函数,a取 [ 0 , + ∞ ) [0,+\infty) [0,+∞)时,阈值函数在硬阈值函数和软阈值函数之间波动。a=0时阈值函数等效于硬阈值函数,a→ + ∞ +\infty +∞时等效于软阈值函数。
本文中设置调节因子a=4。
wname='sym4';%选sym4小波基
lev=5;%5层分解
[c,l]=wavedec(s,lev,wname);
a5=appcoef(c,l,wname,lev);%提取低频系数
d5=detcoef(c,l,5);%提取高频系数
d4=detcoef(c,l,4);
d3=detcoef(c,l,3);
d2=detcoef(c,l,2);
d1=detcoef(c,l,1);
a=4;%设置调节因子
cD=[d1,d2,d3,d4,d5];
sigma=median(abs(cD))/0.6745;%cD为处理后的高频小波系数
thr1=(sigma*sqrt(2*(log(length(y)))))/(log(1+1));
for i=1:length(d1)
if(d1(i)>=thr1)
cD1(i)=d1(i)-thr1/(1+exp(((d1(i)-thr1).^2)/a))-thr1/(2*exp(1/a));%估计第一层小波系数
else if(abs(d1(i))<thr1)
cD1(i)=0;
else
cD1(i)=d1(i)+thr1/(1+exp(((-d1(i)-thr1).^2)/a))+thr1/(2*exp(1/a));
end
end
end
thr2=(sigma*sqrt(2*(log(length(y)))))/(log(2+1));
for i=1:length(d2)
if(d2(i)>=thr2)
cD2(i)=d2(i)-thr2/(1+exp(((d2(i)-thr2).^2)/a))-thr2/(2*exp(1/a));%估计第二层小波系数
else if(abs(d2(i))<thr2)
cD2(i)=0;
else
cD2(i)=d2(i)+thr2/(1+exp(((-d2(i)-thr2).^2)/a))+thr2/(2*exp(1/a));
end
end
end
thr3=(sigma*sqrt(2*(log(length(y)))))/(log(3+1));
for i=1:length(d3)
if(d3(i)>=thr3)
cD3(i)=d3(i)-thr3/(1+exp(((d3(i)-thr3).^2)/a))-thr3/(2*exp(1/a));%估计第三层小波系数
else if(abs(d3(i))<thr3)
cD3(i)=0;
else
cD3(i)=d3(i)+thr3/(1+exp(((-d3(i)-thr3).^2)/a))+thr3/(2*exp(1/a));
end
end
end
thr4=(sigma*sqrt(2*(log(length(y)))))/(log(4+1));
for i=1:length(d4)
if(d4(i)>=thr4)
cD4(i)=d4(i)-thr4/(1+exp(((d4(i)-thr4).^2)/a))-thr4/(2*exp(1/a));%估计第四层小波系数
else if(abs(d4(i))<thr4)
cD4(i)=0;
else
cD4(i)=d4(i)+thr4/(1+exp(((-d4(i)-thr4).^2)/a))+thr4/(2*exp(1/a));
end
end
end
thr5=(sigma*sqrt(2*(log(length(y)))))/(log(5+1));
for i=1:length(d5)
if(d5(i)>=thr5)
cD5(i)=d5(i)-thr5/(1+exp(((d5(i)-thr5).^2)/a))-thr5/(2*exp(1/a));%估计第五层小波系数
else if(abs(d5(i))<thr5)
cD5(i)=0;
else
cD5(i)=d5(i)+thr5/(1+exp(((-d5(i)-thr5).^2)/a))+thr5/(2*exp(1/a));
end
end
end
%开始重构
cd=[a5,cD5,cD4,cD3,cD2,cD1];
c=cd;
yhs=waverec(cd,l,wname);
六、各阈值函数、阈值估计方法的去噪效果
软、硬两种阈值函数和 s q t w o l o g 、 r i g r s u r e 、 h e u r s u r e 、 m i n i m a x i sqtwolog、rigrsure、heursure、minimaxi sqtwolog、rigrsure、heursure、minimaxi四种阈值估计方法两两组合,形成8种去噪算法,与上节提出的改进算法进行比较,比较它们的去噪性能,验证改进算法的有效性。
1、生成去噪效果图
xdh1=wden(s,'sqtwolog','h','mln',M1,wavec);
figure(5)
subplot(211);
plot(xdh1);
xlabel('样本序号');
ylabel('幅值');
title('sqtwolog阈值+硬阈值函数去噪法效果图');
xds1=wden(s,'sqtwolog','s','mln',M1,wavec);
subplot(212);
plot(xds1);
xlabel('样本序号');
ylabel('幅值');
title('sqtwolog阈值+软阈值函数去噪法效果图');
xdh2=wden(s,'rigrsure','h','mln',M2,wavec);
figure(6)
subplot(211);
plot(xdh2)
xlabel('样本序号');
ylabel('幅值');
title('rigrsure阈值+硬阈值函数去噪法效果图');
xds2=wden(s,'rigrsure','s','mln',M2,wavec);
subplot(212);
plot(xds2);
xlabel('样本序号');
ylabel('幅值');
title('rigrsure阈值+软阈值函数去噪法效果图');
xdh3=wden(s,'heursure','h','mln',M3,wavec);
figure(7)
subplot(211);
plot(xdh3);
xlabel('样本序号');
ylabel('幅值');
title('heursure阈值+硬阈值函数去噪法效果图');
xds3=wden(s,'heursure','s','mln',M3,wavec);
subplot(212);
plot(xds3);
xlabel('样本序号');
ylabel('幅值');
title('heursure阈值+软阈值函数去噪法效果图');
xdh4=wden(s,'minimaxi','h','mln',M4,wavec);
figure(8)
subplot(211);
plot(xdh4);
xlabel('样本序号');
ylabel('幅值');
title('minimaxi阈值+硬阈值函数去噪法效果图');
xds4=wden(s,'minimaxi','s','mln',M4,wavec);
subplot(212);
plot(xds4);
xlabel('样本序号');
ylabel('幅值');
title('minimaxi阈值+软阈值函数去噪法效果图');
figure(9)
subplot(211);
plot(yhs,'LineWidth',1);
xlabel('样本序号');
ylabel('幅值');
title('改进的阈值去噪法效果图');
2、计算去噪后信噪比
snrxn=snrr(y,s);
fprintf(' 原加噪信号信噪比 %4.4f\n',snrxn);
snrxdh1=snrr(y,xdh1);
fprintf(' sqtwolog阈值+硬阈值函数去噪信噪比 %4.4f\n',snrxdh1);
snrxdh1=snrr(y,xds1);
fprintf(' sqtwolog阈值+软阈值函数去噪信噪比 %4.4f\n',snrxdh1);
snrxdh2=snrr(y,xdh2);
fprintf(' rigrsure阈值+硬阈值函数去噪信噪比 %4.4f\n',snrxdh2);
snrxds2=snrr(y,xds2);
fprintf(' rigrsure阈值+软阈值函数去噪信噪比 %4.4f\n',snrxds2);
snrxdh3=snrr(y,xdh3);
fprintf(' heursure阈值+硬阈值函数去噪信噪比 %4.4f\n',snrxdh3);
snrxds3=snrr(y,xds3);
fprintf(' heursure阈值+软阈值函数去噪信噪比 %4.4f\n',snrxds3);
snrxdh4=snrr(y,xdh4);
fprintf(' minimaxi阈值+硬阈值函数去噪信噪比 %4.4f\n',snrxdh4);
snrxds4=snrr(y,xds4);
fprintf(' minimaxi阈值+软阈值函数去噪信噪比 %4.4f\n',snrxds4);
snrys=snrr(y,yhs);
fprintf(' 改进后的信噪比 %4.4f\n',snrys);
参考文献
范小龙,谢维成,蒋文波,李毅,黄小莉.一种平稳小波变换改进阈值函数的电能质量扰动信号去噪方法[J].电工技术学报,2016,31(14):219-226.