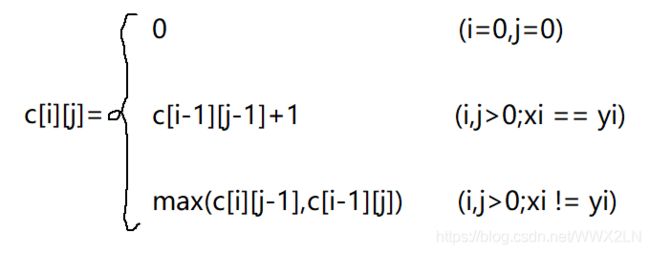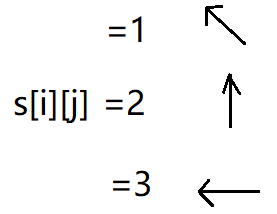动态规划——最长公共子序列LCS

一、动态规划算法

动态规划算法与分治法类似，其基本思想也是将带求解问题分解成若干个子问题，先求解子问题，然后从这些子问题的解得到原问题的解。

与分治法不同的是,适合于用动态规划法求解的问题,经分解得到的子问题往往不是互相独立的。若用分治法解这类问题,则分解得到的子问题数目太多,以至于最后解决原问题需要耗费指数时间。然而，不同子问题的数目常常只有多项式量级。在用分治法求解时,有些子问题被重复计算了许多次。

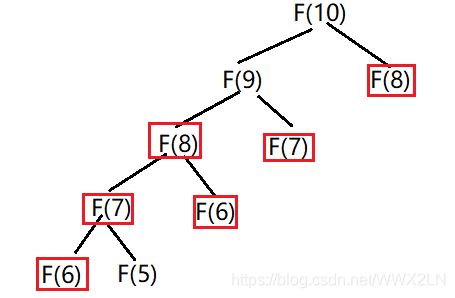
如我们求解斐波那契数列时：

int Fibonacci(int n)
{
	if(n<=0)
		return 0;
	if(n==1)
		return 1;
	return Fibonacci(n-1)+Fibonacci(n-2);
}

思路：

如图，需要重复计算某些已经解决的答案。如果能够保存已解决的子问题的答案,而在需要时再找出已求得的答案,就可以避免大量重复计算,从而得到多项式时间算法。为了达到这个目的,可以用一个表来记录所有已解决的子问题的答案。不管该子问题以后是否被用到,只要它被计算过,就将其结果填人表中。这就是动态规划法的基本思想。具体的动态规划算法是多种多样的,但它们具有相同的填表格式。

动态规划算法适合于解最优化问题，通常可以按照以下步骤：

（1）找出最优解的性质，并刻画其结构特征；

（2）递归的定义最优值；

（3）以自底向上的方式计算出最优值；

（4）根据计算最优值时得到的信息，构造最优解

步骤(1)~(3)是动态规划算法的基本步骤。在只需要求出最优值的情形,步骤(4)可以省去。若需要求问题的最优解,则必须执行步骤(4)。此时，在步骤(3)中计算最优值时,通常需记录更多的信息,以便在步骤(4)中，根据所记录的信息,快速构造出最优解。
下面运用动态规划算法来求解最长公共子序列问题，和矩阵连乘问题

二、最长公共子序列

问题描述：给定两个序列X和Y,当另一序列Z既是X的子序列又是Y的子序列时,称Z是序列X和Y的公共子序列，并且子序列指的是严格意义上的下标递增的序列。现给出两个序列X{ABCBDAB},Y{BDCABA},其最长公共子序列就是{BDAB}。下面给出求解最长公共子序列的算法。

思路：设序列X的长度为i，序列Y的长度为j，则二者最长公共子序列C(i,j)可表示为：

分三种情况：

（1）当i=0或j=0时，c(i,j)=0;

（2）当X[i]=Y[j]时，c(i,j)=c(i-1,j-1)+1；//即当两个序列的最后一个字符相同时，算最长公共子序列就是算除去最后一个字符，其前面部分的最长公共子序列的结果+1

（3）当X[i]!=Y[j]时，c(i,j)=max{c(i-1,j),c(i,j-1)}；//当二者最后一个不相等时，其最长公共子序列的值是二者中任意一个长度-1与另一个比较的最长公共子序列中的最大值

即：

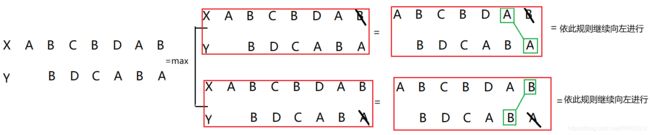
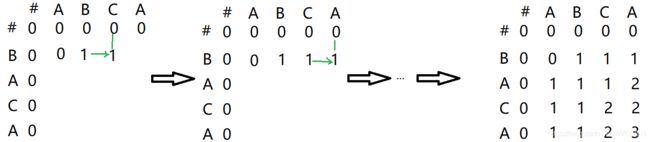
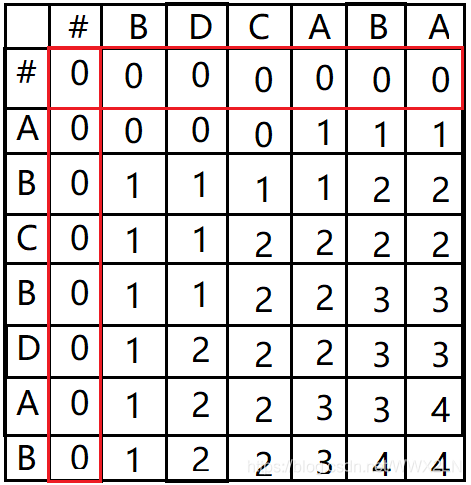
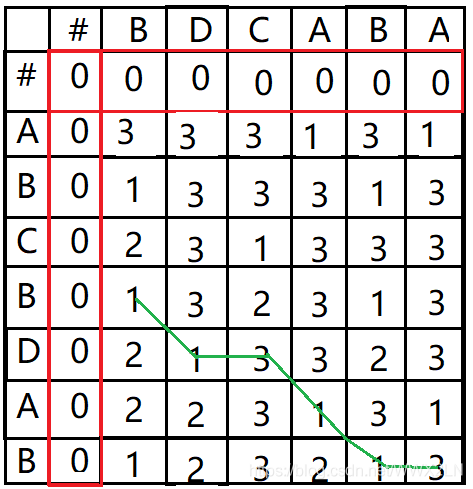
下面以序列{A,B,C,A}和序列{B,A,C,A}为例，展示填表的详细过程：

填表规则：当该位置对应的X序列的值与Y序列的值不相同，该位置就填其左方和上方中较大的值；若相同，就填其左上方的值+1

通过上述方式，在本例最终会得到一个表示到目前为止最长公共子序列的长度的表C：

和标识找到最长公共子序列的路线表S：

 

代码：

/*
c[i][j]存储Xi和Yi的最长公共子序列的长度；
b[i][j]记录c[i][j]的值是由哪一个子问题的解得到的，这在构造最长公共子序列时要用到
问题的最优解，即X和Y的最长公共子序列的长度记录于c[m][n]中,
为了方便编写代码，在下面代码中给X和Y序列的最前面都加上一个字符"#"，因此数组c和b大小都是（m+1）*(n+1)的,
第0行和第0列初始化为0
*/
void InitArray(vector > &c, int row,int col)
{
	c.resize(row);
	for(int i = 0;i >&c,vector >&b)
{
	if(i < 1 || j < 1) return 0;
	if(c[i][j] > 0) return c[i][j];
	if(x[i] == y[j]) 
	{
		c[i][j] =  LCSLength(i-1,j-1,x,y,c,b) + 1;
		b[i][j] = 1;
	}
	else
	{
		int max1 = LCSLength(i-1,j,x,y,c,b);
		int max2 = LCSLength(i,j-1,x,y,c,b);
		if(max1 > max2)
		{
			c[i][j] = max1;
			b[i][j] = 2;
		}
		else
		{
			c[i][j] = max2;
			b[i][j] = 3;
		}
	}
	return c[i][j];
}
//法二：非递归
int NiceLCSLength(int m,int n,string &x,string &y,vector> &c,vector> &b)//时间复杂度O(m*n)
{
	for(int i = 0;i<=m;++i) c[i][0] = 0;
	for(int i = 0;i<=n;++i) c[0][i] = 0;
	for(int i=1;i<=m;++i)
	{
		for(int j=1;j<=n;++j)
		{
			if(x[i]==y[j])
			{
				c[i][j]=c[i-1][j-1]+1;
				b[i][j]=1;//1是向左上走
			}    
			else if(c[i-1][j]>c[i][j-1])
			{
				c[i][j]=c[i-1][j];
				b[i][j]=2;//2是向上走
			}
			else
			{
				c[i][j]=c[i][j-1];
				b[i][j]=3;//3是向左走
			}
		}
	}
	return c[m][n];
}
//最后递归子问题
void LCS(int i,int j,string& x,vector>&b)
{
	if(i==0 || j==0)
	{
		return;
	}
	if(b[i][j]==1)
	{
		LCS(i-1,j-1,x,b);
		cout<< x[i]<<" ";
	}
	else if(b[i][j]==2)
	{
		LCS(i-1,j,x,b);
	}
	else
	{
		LCS(i,j-1,x,b);
	}
}
void Printf(vector>&b)
{
	for(int i=0;i>c;//最优解数组
	vector>b;//通过该数组中存的数值1,2,3可以找到最终的公共子序列并打印
	InitArray(c,m,n);
	InitArray(b,m,n);
	int res=NiceLCSLength(m-1,n-1,x,y,c,b);
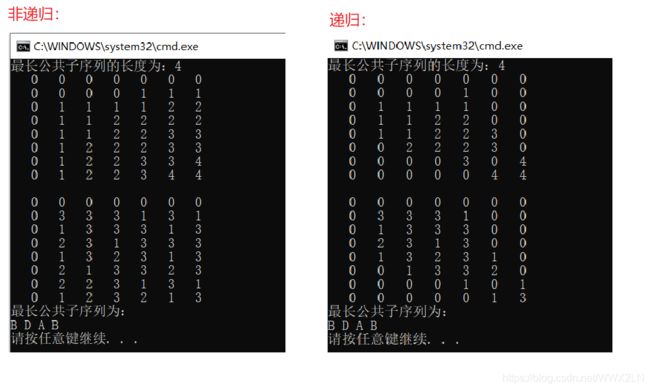
	cout<<"最长公共子序列的长度为："<

运行结果如下图：

扩展小知识： 

在写该代码时，主要逻辑理清楚了后就不难，但是本人在调试的过程中，发现了一些自己原来并没有注意到的问题。

一开始我只定义了二维数组c和b，并未声明其大小，我心里清楚m和n就是行和列的边界大小，在初始化时，也是直接利用下标操作这样初始化的，但是运行时就一直出现“vector subscript out of range”的错误。

查了资料才发现，在使用vector时，利用下标进行插入操作是非法的，必须使用vector里的push_back()方法，vector的下标操作只能用于修改容器中数组元素，不能用于插入元素，若非要用下标来进行操作，必须保证初始化容器的时候有足够的元素，但这种方法严格来说属于修改元素值而不是插入。

本代码中，就是先写了个InitArray()将容器初始化为0，再在后面根据实际情况利用下标进行修改对应元素的值。

这个小问题的发现和解决着实花了很长时间，真的是只有在实践过程中才会发现的点。