机器学习——自相似矩阵（Self-Similarity Matrix，SSM）

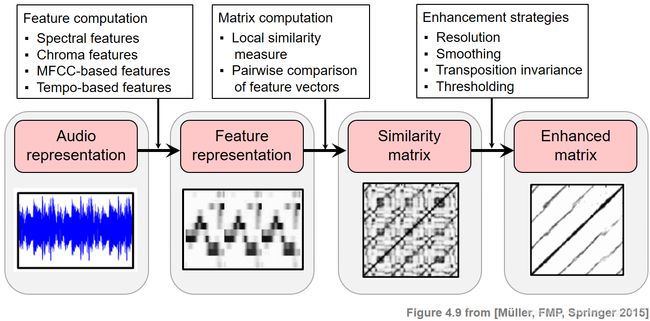
研究音乐结构及其相互关系的一般思路是将音乐信号转换为合适的特征序列，然后将特征序列中的每个元素与序列中的所有其他元素进行比较。这就产生了一种自相似矩阵(SSM)，它不仅对音乐结构分析具有重要意义，而且对多种时间序列的分析也具有重要意义。

基本定义

设F为特征空间，$s:F\times F\to R$为使$x,y\in F$两个元素可以比较的相似性度量。一般情况下，当元素$x,y\in F$相似时，$s(x,y)$值较高，否则值较小。给定一个特征序列$X=(x_1,x_2，\dots ，x_N)$，其思想是将序列中的所有元素相互比较。由此得到由定义的$N$平方自相似矩阵$S\in R^{N\times N}$为：
$$S(n,m):=s(x_n,x_m)$$
其中，$n,m\in [1:n]，x_n,x_m\in F$。在下文中，$(n,m)\in [1:n]\times [1:n]$也称为S的一个单元，$S(n,m)$的值称为单元$(n,m)$的取值。根据应用程序上下文和用于比较数据的概念，有许多不同名称下的相关概念，如递归图、代价矩阵或自距离矩阵等等。在本笔记本中，我们只考虑自相似矩阵，但是要解释的技术可以很容易地转移到其他类型的矩阵。

通常，我们假设特征空间是某个维数$K\in N$的欧几里德空间$F=R^K$。例如，一个简单的相似度度量$s$是由内积定义：
$$s(x,y):=⟨x,y⟩$$
对于两个向量$x,y\in F$。通过这种相似性度量，两个正交特征向量之间的得分为零，否则为非零。当特征向量对欧几里德范数进行归一化时，相似值$s(x,y)$位于区间$[-1,1]$。在这种情况下，给定特征序列$X=(x_1，x_2，\dots ，x_n)$的归一化特征中，对于所有$n个\in [1：n]$，假设在$s(x_n，x_n)=1$的情况下，SSM中的最大值被假定。因此，得到的SSM具有较大的对角线值。更一般地，给定特征序列的重复模式在SSM中以具有大相似值的结构的形式变得可见。

在下面的示例中，我们生成归一化特征向量的合成特征序列。特征向量的维数为$K=4$，序列长度为$N=500$。图中显示了功能序列以及生成的SSM。

Important notes:

• 在可视化SSM时，颜色映射表Cmap的选择可能会对插图的整体外观产生重大影响。选择合适的色彩映射表有助于直观地突出显示SSM的某些属性。
• 当使用如上所述的归一化特征的特征序列和相似性度量时，可以通过简单的矩阵-矩阵乘积来计算SSM。更准确地说，如果特征序列由$K\times N$矩阵$X$实现，则SSM中$S$由$S=X^{T}X$给出。
• 此外，我们经常假设特征向量的所有条目都是正的。在这种情况下，值$s(x_n，x_m)$也是正数，并且位于区间$[0，1]$内。

import numpy as np
import os, sys, librosa
from scipy import signal
from matplotlib import pyplot as plt
import matplotlib.gridspec as gridspec
import IPython.display as ipd
import pandas as pd
from numba import jit

sys.path.append('..')
import libfmp.b
import libfmp.c2
import libfmp.c3
import libfmp.c4
import libfmp.c6

%matplotlib inline

# Generate normalized feature sequence
K = 4
M = 100
r = np.arange(M)
b1 = np.zeros((K,M))
b1[0,:] = r
b1[1,:] = M-r
b2 = np.ones((K,M))
X = np.concatenate(( b1, b1, np.roll(b1, 2, axis=0), b2, b1 ), axis=1)
X = libfmp.c3.normalize_feature_sequence(X, norm='2', threshold=0.001)

# Compute SSM
S = np.dot(np.transpose(X), X)

# Visualization
cmap = 'gray_r'
fig, ax = plt.subplots(2, 2, gridspec_kw={'width_ratios': [1, 0.05], 
                                          'height_ratios': [0.2, 1]}, figsize=(4.5, 5))
libfmp.b.plot_matrix(X, Fs=1, ax=[ax[0,0], ax[0,1]], cmap=cmap,
            xlabel='Time (frames)', ylabel='', title='Feature sequence')
libfmp.b.plot_matrix(S, Fs=1, ax=[ax[1,0], ax[1,1]], cmap=cmap,
            title='SSM', xlabel='Time (frames)', ylabel='Time (frames)', colorbar=True);
plt.tight_layout()

通过适当调整色彩映射表，可以改变视觉外观。例如，将颜色分布移向较浅的颜色可以增强可视化中的路径结构。

cmap = libfmp.b.compressed_gray_cmap(alpha=-1000)
fig, ax = plt.subplots(2, 2, gridspec_kw={'width_ratios': [1, 0.05], 
                                          'height_ratios': [0.2, 1]}, figsize=(4.5, 5))
libfmp.b.plot_matrix(X, Fs=1, ax=[ax[0,0], ax[0,1]], cmap=cmap,
            xlabel='Time (frames)', ylabel='', title='Feature sequence')
libfmp.b.plot_matrix(S, Fs=1, ax=[ax[1,0], ax[1,1]], cmap=cmap,
            title='SSM', xlabel='Time (frames)', ylabel='Time (frames)', colorbar=True);
plt.tight_layout()

块和路径结构

如上例所示，SSMs中最突出的两个结构称为块和路径。如果特征序列捕获在整个音乐部分的持续时间内保持某种恒定的音乐属性，则每个特征向量与该片段内的所有其他特征向量相似。因此，整个大值块都会出现在SSM中。换句话说，同质性属性对应于块状结构。如果特征序列包含两个重复子序列(例如，对应于同一旋律的两个片段)，则两个子序列的对应元素彼此相似。结果，在SSM中可以看到平行于主对角线的高度相似的路径(或条纹)。换句话说，重复属性对应于路径状结构。

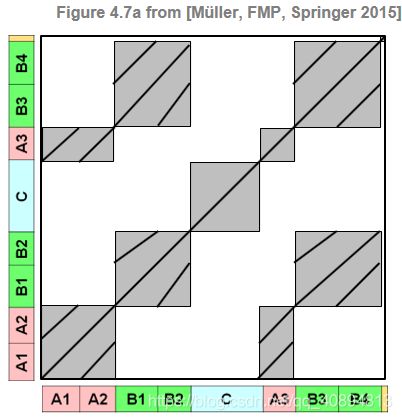
作为一个例子，下图显示了约翰尼斯·勃拉姆斯(Johannes Brahms)为匈牙利舞蹈5号创作的理想化SSM，其音乐结构为$A_1{A}_2{B}_1{B}_{2}C{A}_3{B}_3{B}_{4}D$。假设三个重复的$A$部分段是同质的，则SSM具有将对应于$A_1{A}_2$的段与其自身相关联的二次块，以及将$A_3$部分段与其自身相关联的另一二次块。此外，还有两个矩形块，一个将$A_1{A}_2$部分段与$A_3$部分段相关联，另一个将$A_3$部分段与$A_1{A}_2$部分段相关联。在三个重复的$A$部分段不同的情况下，SSM显示(或多或少)平行于主对角线的路径结构。例如，存在将$A_1$与$A_2$关联的路径和将$A_1$与$A_3$关联的路径，该路径具有较大的相似度值。

基于色谱图特征的SSM

下面的代码使用色度谱图作为特征表示，从Brahms的匈牙利舞的录音中生成SSM。在可视化中，较大的$S$值由深灰色表示，较小的值由浅灰色表示。实际上，在这种情况下得到的SSM在很大程度上类似于理想化的SSM。与$A$声部音段相对应的块状结构表明，这些音段在和声方面是相当均匀的。同样的道理也适用于$C$部分。此外，$C$部分块(即，将$C$部分帧与其他段的帧相关联的所有单元)之外的小相似值表明$C$部分段与所有其他部分在谐和上或多或少是无关的。对于$B$部分，有路径状结构，没有块状结构。这表明$B$部分片段共享相同的和声级数(即，在和声方面是重复的)，但在和声方面不是均匀的。

@jit(nopython=True)
def compute_sm_dot(X, Y):
    """Computes similarty matrix from feature sequences using dot (inner) product

    Notebook: C4/C4S2_SSM.ipynb

    Args:
        X (np.ndarray): First sequence
        Y (np.ndarray): Second Sequence

    Returns:
        S (float): Dot product
    """
    S = np.dot(np.transpose(X), Y)
    return S

def plot_feature_ssm(X, Fs_X, S, Fs_S, ann, duration, color_ann=None,
                     title='', label='Time (seconds)', time=True,
                     figsize=(5, 6), fontsize=10, clim_X=None, clim=None):
    """Plot SSM along with feature representation and annotations (standard setting is time in seconds)

    Notebook: C4/C4S2_SSM.ipynb

    Args:
        X: Feature representation
        Fs_X: Feature rate of ``X``
        S: Similarity matrix (SM)
        Fs_S: Feature rate of ``S``
        ann: Annotaions
        duration: Duration
        color_ann: Color annotations (see :func:`libfmp.b.b_plot.plot_segments`) (Default value = None)
        title: Figure title (Default value = '')
        label: Label for time axes (Default value = 'Time (seconds)')
        time: Display time axis ticks or not (Default value = True)
        figsize: Figure size (Default value = (5, 6))
        fontsize: Font size (Default value = 10)
        clim_X: Color limits for matrix X (Default value = None)
        clim: Color limits for matrix ``S`` (Default value = None)

    Returns:
        fig: Handle for figure
        ax: Handle for axes
    """
    cmap = libfmp.b.compressed_gray_cmap(alpha=-10)
    fig, ax = plt.subplots(3, 3, gridspec_kw={'width_ratios': [0.1, 1, 0.05],
                                              'wspace': 0.2,
                                              'height_ratios': [0.3, 1, 0.1]},
                           figsize=figsize)
    libfmp.b.plot_matrix(X, Fs=Fs_X, ax=[ax[0, 1], ax[0, 2]], clim=clim_X,
                         xlabel='', ylabel='', title=title)
    ax[0, 0].axis('off')
    libfmp.b.plot_matrix(S, Fs=Fs_S, ax=[ax[1, 1], ax[1, 2]], cmap=cmap, clim=clim,
                         title='', xlabel='', ylabel='', colorbar=True)
    ax[1, 1].set_xticks([])
    ax[1, 1].set_yticks([])
    libfmp.b.plot_segments(ann, ax=ax[2, 1], time_axis=time, fontsize=fontsize,
                           colors=color_ann,
                           time_label=label, time_max=duration*Fs_X)
    ax[2, 2].axis('off'), ax[2, 0].axis('off')
    libfmp.b.plot_segments(ann, ax=ax[1, 0], time_axis=time, fontsize=fontsize,
                           direction='vertical', colors=color_ann,
                           time_label=label, time_max=duration*Fs_X)
    return fig, ax

# Waveform
fn_wav = os.path.join('..', 'data', 'C4', 'FMP_C4_Audio_Brahms_HungarianDances-05_Ormandy.wav')
Fs = 22050
x, Fs = librosa.load(fn_wav, Fs) 
x_duration = (x.shape[0])/Fs

# Chroma Feature Sequence
N, H = 4096, 1024
chromagram = librosa.feature.chroma_stft(y=x, sr=Fs, tuning=0, norm=2, hop_length=H, n_fft=N)
X, Fs_X = libfmp.c3.smooth_downsample_feature_sequence(chromagram, Fs/H, filt_len=41, down_sampling=10)

# Annotation
filename = 'FMP_C4_Audio_Brahms_HungarianDances-05_Ormandy.csv'
fn_ann = os.path.join('..', 'data', 'C4', filename)
ann, color_ann = libfmp.c4.read_structure_annotation(fn_ann, fn_ann_color=filename)
ann_frames = libfmp.c4.convert_structure_annotation(ann, Fs=Fs_X) 

# SSM 
X = libfmp.c3.normalize_feature_sequence(X, norm='2', threshold=0.001)
S = compute_sm_dot(X,X)
fig, ax = plot_feature_ssm(X, 1, S, 1, ann_frames, x_duration*Fs_X, color_ann=color_ann,
                           clim_X=[0,1], clim=[0,1], label='Time (frames)',
                           title='Chroma feature (Fs=%0.2f)'%Fs_X)

SSM Based on MFCC Features

接下来，我们根据MFCC特征计算SSM。使用该表示的所有$K=20$的MFCC系数导致主要具有块状结构的SSM。特别地，可以观察到大致对应于A部分和C部分的块。实际上，块结构由MFCC特征的前两个(较低)系数主导。仅考虑系数4到14会导致SSM具有更精细的块结构，并且还揭示出路径状结构。

Important notes:

• 在计算SSM之前，我们通过应用带有后续下采样的平均滤波器进行了一些平滑处理。平滑抑制了特征序列中的小局部波动，并且可能对所得到的SSM具有显著影响。
• 注意，对特征序列下采样系数$H$，在计算SSM的$S$时将效率提高到$H_2$的系数。
• 由于MFCC特征的值可以是负值，因此SSM值也可以是负值(在归一化MFCC特征之后的间隔$[1,-1]$中)。

from libfmp.b import FloatingBox
float_box = libfmp.b.FloatingBox()

# MFCC-based feature sequence
N, H = 2048, 1024
X_MFCC = librosa.feature.mfcc(y=x, sr=Fs, hop_length=H, n_fft=N)
coef = np.arange(0,20)
X_MFCC_upper = X_MFCC[coef,:]
X, Fs_X = libfmp.c3.smooth_downsample_feature_sequence(X_MFCC_upper, Fs/H, filt_len=41, down_sampling=10)
X = libfmp.c3.normalize_feature_sequence(X, norm='2', threshold=0.001)
S = compute_sm_dot(X,X)
ann_frames = libfmp.c4.convert_structure_annotation(ann, Fs=Fs_X) 
fig, ax = plot_feature_ssm(X, 1, S, 1, ann_frames, x_duration*Fs_X, color_ann=color_ann,
    title='MFCC (20 coefficients, Fs=%0.2f)'%Fs_X, label='Time (frames)')
float_box.add_fig(fig)


# MFCC-based feature sequence only using coefficients 4 to 14
coef = np.arange(4,15)
X_MFCC_upper = X_MFCC[coef,:]
X, Fs_X = libfmp.c3.smooth_downsample_feature_sequence(X_MFCC_upper, Fs/H, filt_len=41, down_sampling=10)
X = libfmp.c3.normalize_feature_sequence(X, norm='2', threshold=0.001)
S = compute_sm_dot(X,X)
ann_frames = libfmp.c4.convert_structure_annotation(ann, Fs=Fs_X) 
fig, ax = plot_feature_ssm(X, 1, S, 1, ann_frames, x_duration*Fs_X, 
                           color_ann=color_ann, label='Time (frames)',
                           title='MFCC (coefficients 4 to 14, Fs=%0.2f)'%Fs_X)
float_box.add_fig(fig)

float_box.show()

SSM Based on Tempogram Features

最后，我们使用循环傅立叶时间图作为底层特征表示来计算SSM。与基于色度的SSM相比，基于时程图的SSM结构不是很清晰。至少，人们可以观察到一个与$C$部分片段相对应的语块，从而强调了它的对比作用。此外，SSM表示在此音乐记录中发生的许多节奏变化。

# Tempogram feature sequence
nov, Fs_nov = libfmp.c6.compute_novelty_spectrum(x, Fs=Fs, N=2048, H=512, gamma=100, M=10, norm=1)
nov, Fs_nov = libfmp.c6.resample_signal(nov, Fs_in=Fs_nov, Fs_out=100)


N, H = 1000, 100
X, T_coef, F_coef_BPM = libfmp.c6.compute_tempogram_fourier(nov, Fs_nov, N=N, H=H, Theta=np.arange(30, 601))
octave_bin = 12
tempogram_F = np.abs(X)
output = libfmp.c6.compute_cyclic_tempogram(tempogram_F, F_coef_BPM, octave_bin=octave_bin)
X = output[0]
F_coef_scale = output[1]
Fs_X = Fs_nov/H
X = libfmp.c3.normalize_feature_sequence(X, norm='2', threshold=0.001)
S = compute_sm_dot(X,X)
ann_frames = libfmp.c4.convert_structure_annotation(ann, Fs=Fs_X) 
fig, ax = plot_feature_ssm(X, 1, S, 1, ann_frames, x_duration*Fs_X, color_ann=color_ann,
    title='Tempogram (Fs=%0.2f)'%Fs_X, label='Time (frames)')

路径和块的形式化定义

我们将segment正式定义为由其起点$s$和终点$t$(根据特征索引给出)指定的集合$\alpha =[s：t]\subseteq [1：n]$。令
$$|\alpha |:=t-s+1$$
表示$\alpha$的长度。接下来，长度为$L$的$\alpha$上的路径是一个序列
$$P=((n_1,m_1),\dots ,(n_L,m_L))$$
其中$(n_{\ell },m_{\ell })\in [1:N{]}^2,\ell \in [1:L]$，满足$M_1=s$，$m_L=t$(boundary condition)和$(n_{\ell +1}，m_{\ell +1})-(n_{\ell }，m_{\ell })\in \Sigma (stepsizecondition)$，其中$\Sigma$表示一组允许的步长。请注意，此定义与warping path 的定义非常相似。在$\Sigma =(1，1)$的情况下，可以得到严格对角线的路径。在下面，我们通常使用集合$\Sigma =(2，1)，(1，2)，(1，1)$。对于路径$P$，可以分别关联由投影${\pi }_1(P)：=[N1：NL]$和${\pi }_2(P)：=[M1：ML]$定义的两个段。边界条件强制${\pi }_2(P)=\alpha$。另一段${\pi }_1(P)$称为诱导段。$P$的得分$\sigma (P)$定义为
$$\sigma (P):=\sum _{\ell =1}^{L}S(n_{\ell },m_{\ell }).$$
注意，segment $\alpha$上的每条路径编码$\alpha$和诱导段之间的关系，其中分数$\sigma (P)$产生该关系的质量度量。对于块，我们也引入了相应的概念。段$\alpha =[s：t]$上的块是一个子集
$$B={\alpha }^{\prime }\times \alpha \subseteq [1:N]\times [1:N]$$
对于某些segment，${\alpha }^{\prime }=[s^{\prime }：t^{\prime }]$。与路径类似，我们为块$B$定义了两个投影${\pi }_1(B)={\alpha }^{\prime }$和${\pi }_2(B)=\alpha$，并将${\alpha }^{\prime }$称为诱导段。此外，我们通过以下公式定义块$B$的得分
$$\sigma (B)=\sum _{(n,m)\in B}S(n,m)$$
路径和块的正式定义如下图所示：

基于路径和块，人们可以考虑不同类型的段之间的相似关系。如果存在高分值的路径$P$，且${\alpha }_1(P)={\alpha }_1$且${\pi }_2(P)={\alpha }_2$，则称段${\pi }_1$与段${\alpha }_2$路径相似。类似地，如果存在得分较高的块$B$，且${\alpha }_1(B)={\alpha }_1$且${\pi }_2(B)={\alpha }_2$，则${\pi }_1$与${\alpha }_2$类似。显然，在相似度量$s$是对称的情况下，自相似矩阵$S$和上面定义的段之间的相似关系也是对称的。相似关系的另一个重要性质是传递性，即如果段${\alpha }_1$类似于段${\alpha }_2$，段${\alpha }_2$类似于段${\alpha }_3$，那么${\alpha }_1$也应该与${\alpha }_3$相似(至少在一定程度上)。此外，在相似性度量s具有该属性的情况下，该属性也适用于路径和块相似性。因此，路径和块结构通常以满足某些对称性和传递性属性的组出现，至少在理想情况下是这样。

音乐结构分析的总体程序

大多数音乐结构分析的计算方法都以这样或那样的方式利用SSM的路径和块状结构，并且整个算法流水线通常包含以下一般步骤：

• 音乐信号被转换成合适的特征序列。
• 基于相似性度量从特征序列计算自相似矩阵。
• 总得分高的块和路径是从SSM派生的。每个块或路径定义一对相似的段。
• 通过应用聚类步骤，从成对关系中形成相互相似的整个片段组。

最后一步可以看作是对由块和路径结构引起的两段关系形成一种传递闭包。

进一步说明

在Brahms的例子中，音乐结构可以通过它的重复结构得到很好的解释。在上图中，当使用基于色度的SSM时，这些结构尤其可见。在接下来的笔记本中，我们将主要关注基于色度的特征来说明音乐结构分析方法。当然，许多技术也可以应用于从其他特征表示获得的SSM。在文献中，通常使用各种特征类型的组合。除了特征类型之外，还有许多方法可以增强SSM的结构特性。如下所示:

• Feature smoothing
• Path enhancemen
• Transposition invariance
• Thresholding
  下图概述了在计算SSM时可以应用的各种策略。
  

This notebook was created by Meinard Müller.
https://www.audiolabs-erlangen.de/fau/professor/mueller