基于有限域Chebyshev多项式的类ElGamal公钥密码算法
文章目录
- 概述
- 论文介绍
-
- 算法描述
- 基于有限域Chebyshev多项式的类ElGamal公钥密码算法实现
-
- 大素数的生成
- 有限域Chebyshev多项式运算的实现
-
- 普通递归法
- 快速递归法
-
- 测试
- 矩阵特征值法
-
- 分析
- 实现
- 测试:
- 算法实现
-
- 密钥产生算法
- 加密算法
- 解密算法
- 算法分析
-
- 三种求ChebyShev多项式的算法的比较
- 改进算法的数值测试
-
- 密钥长度为64位
- 密钥长度为128位
- 论文中的一些错误
-
- 数据错误
- 矩阵特征值求Chebyshev多项式的值
-
- 我的解决办法
- 源代码
概述
复现论文:《基于混沌理论的非对称加密算法研究》
复现算法:基于有限域Chebyshev多项式的类ElGamal公钥密码算法
编程语言:Python
采用论文中的方法:
- 矩阵特征值法赋值ChebyShev多项式
- 素数生成Miller-Rabin算法
库依赖:
- 需要下载第三方库gmpy2库
- 这个库实现了求e模p的逆元
- 求逆元操作直接导入库了
代码文件组成:
- alogrithm.py公钥算法文件
- Miller-Rabin.py素性检验算法
- 赋值ChebyShev多项式的方法
- common_method.py 普通递归法
- quick_method.py快速递归法
- charactor_method.py 矩阵特征值法
- test.py:是分析三种方法的效率的程序
程序运行方式:根据命令行提示进行输入数据
不足或改进之处:命令行输入不方便,可以写一个GUI程序
论文介绍
论文中主要叙述的三种算法,
- 基于Chebyshev多项式的类ElGamal公钥密码算法
- 基于有限域Chebyshev多项式的类ElGamal公钥密码算法
- 改进的基于有限域Chebyshev多项式的类ElGamal公钥密码算法
Chebyshev多项式
T p + 1 = 2 x T p ( x ) − T p − 1 ( x ) , p ≥ 2 , T 1 = x T_{p+1}=2xT_p(x)-T_{p-1}(x),p\geq2,T_1=x Tp+1=2xTp(x)−Tp−1(x),p≥2,T1=x
一个显著的星光值是其班群特性
T r ( T s ( x ) ) = T r s ( x ) , r , s ∈ Z T_r(T_s(x))=T_{rs}(x), r,s \in Z Tr(Ts(x))=Trs(x),r,s∈Z
满足复合律
T s ( T r ( x ) ) = T r ( T s ( x ) ) , r , s ∈ Z T_s(T_r(x))=T_r(T_s(x)),r,s\in Z Ts(Tr(x))=Tr(Ts(x)),r,s∈Z
有限域Chebyshev多项式
定义:令 n ∈ Z + n\in Z^+ n∈Z+,变量 x ∈ Z p x\in Z_p x∈Zp,则多项式 T n ( x ) : Z p − > Z p T_n(x):Z_p -> Z_p Tn(x):Zp−>Zp的递推关系定义为:
T p + 1 = ( 2 x T p ( x ) − T p − 1 ( x ) ) ( m o d P ) , n ≥ 2 T_{p+1}=(2xT_p(x)-T_{p-1}(x))(mod\;P),n\geq2 Tp+1=(2xTp(x)−Tp−1(x))(modP),n≥2,且有 T 0 ( X ) ≡ 1 ( m o d p ) T_0(X)\equiv1(mod\;p) T0(X)≡1(modp) T 1 ( X ) ≡ x ( m o d p ) T_1(X)\equiv x(mod\;p) T1(X)≡x(modp)
算法描述
设N=P*Q,P和Q为两个大素数,则有(A mod N)(mod P)=A(mod P)。根据这一性质,本章提出了一种改进的基于有限域Chebyshev多项式的类ELGamal公钥密码算法。改进后的算法同样有密钥残生算法,加密算法和机密算法构成。
密钥产生算法:(Alice需要产生密钥)
- 产生一个大的随机数P和Q,计算N=P*Q;
- 随机残生一个大整数x,是的x
- 随机残生一个随机数2<=s
- Alice的公开密钥为(x,N,A),密钥为(S,P)
- 随机残生一个随机数2<=s
加密算法:(Bob需要将明文m加密)
- 获得Alice的公开密钥(x,N,A);
- 将m看做一个整数并将m分段,使得m属于Zp,0
- 选择一个随机整数2<=r
- 计算B=Tr(x)(mod N)和X=m*Tr(A)(mod N);
- 将密文消息(B,X)传给Alice。
- 选择一个随机整数2<=r
解密算法:(Alice需要将密文c还原成m)
- 使用密钥P计算C=B(mod P)
- 使用密钥s计算D=Ts©(mod P)
- 计算m=X*D-1(mod P)恢复明文m。
基于有限域Chebyshev多项式的类ElGamal公钥密码算法实现
大整数的实现
因为编程语言是python,所以不需要考虑大整数的存储和运算。
大素数的生成
论文中使用的是很容易实现并且广泛应用的简单算法——Miller-Rabin素性测试法。本身算法不难
代码如下:
import random
def quickPowMod(a,n,m):
re = 1
base = a % m
while(n>0):
temp = n&1
if (temp):
re = (re*base) % m
base = (base*base) % m
n >>= 1
return re
def Miler_Rabin(P,m=15):
flag = 0
for _ in range(0, m):
a = random.randint(2, P-1)
temp = quickPowMod(a,P-1,P)
if temp != 1:
flag = 1
break
if flag == 0:
print("{} 是素数".format(P))
else:
print("{} 不是素数".format(P))
有限域Chebyshev多项式运算的实现
普通递归法
根据Chebyshev多项式的性质和定义,可以得到:
T 2 n = T 2 ( T n ( x ) ) T 2 n + 1 = 2 T n + 1 T n ( x ) − x T_{2n}=T_2(T_n(x)) \\ T_{2n+1}=2T_{n+1}T_n(x)-x T2n=T2(Tn(x))T2n+1=2Tn+1Tn(x)−x
应用到Chebyshev多项式的赋值运算中,得到:
当n为偶数时:
T n = 2 T n / 2 2 − 1 T_n=2T^2_{n/2}-1 Tn=2Tn/22−1
n为奇数时
T n = 2 T n + 1 / 2 T n − 1 / 2 − x T_n=2T_{n+1/2}T_{n-1/2}-x Tn=2Tn+1/2Tn−1/2−x
import time
import doctest
def func(n,x,p):
'''
>>> func(155033642076,8909654478045,431084178421767)
290588719813696
'''
if n==0:
return 1
elif n==1:
return x
elif n%2==0:
temp=func(n//2,x,p)
re=2*temp*temp-1
return re%p
else:
re=2*func((n+1)//2,x,p)*func((n-1)//2,x,p)-x
return re%p
测试数据:func(155033642076,8909654478045,431084178421767)
输出
290588719813696
耗时: 2.061542510986328
快速递归法
流程对整数n,有:
- 首先计算偶数部分,得到A
- 计算奇数部分的时候重复利用A
根据递归函数的思想,首先判断n的值是否为0,若为0,则满足递归程序的出口条件,返回值1,若n为1返回值x;否则判断n是否为偶数:若为偶数,则n/2递归。为奇数时还需要判断模4为1还是3,然后根据结果进行相应的递归。
def func(n,x,p):
if n==0:
return 1
elif n==1:
return x
elif n%2==0:#偶数
temp=func(n//2,x,p)
return (2*temp*temp-1)%p
else:
if n%4==1:
odd=(n+3)//4
even=(n-1)//4#偶数
else:
odd=(n-3)//4
even=(n+1)//4
A=func(even,x,p)
B=func(odd,x,p)
C=(2*A*A-1)%p
D=(2*A*B-x)%p
return (2*C*D-x)%p
测试
测试数据
n=155033642076
x=8909654478045
p=431084178421767
调用函数
func(155033642076,8909654478045,431084178421767)
输出
290588719813696
耗时: 0.01200246810913086
与普通递归法相比快速递归法赋值ChebyShev多项式在速度上快了20几倍
矩阵特征值法
分析
将有限域Chebyshev多项式的表达式协程表达式:
( T n T n + 1 ) = ( 0 1 − 1 2 x ) . ( T n − 1 T n ) ( m o d P ) = ( 0 1 − 1 2 x ) n ( T 0 T 1 ) ( m o d P ) = A n . ( T 0 T 1 ) ( m o d P ) \begin{pmatrix}T_n\\T_{n+1}\end{pmatrix}=\begin{pmatrix}0&1\\-1&2x\end{pmatrix}.\begin{pmatrix}T_{n-1}\\T_{n}\end{pmatrix}(mod\;P)=\begin{pmatrix}0&1\\-1&2x\end{pmatrix}^n\begin{pmatrix}T_0\\T_1\end{pmatrix}(mod\;P)=A^n.\begin{pmatrix}T_0\\T_1\end{pmatrix}(mod\;P) (TnTn+1)=(0−112x).(Tn−1Tn)(modP)=(0−112x)n(T0T1)(modP)=An.(T0T1)(modP)
设 a = x 2 − 1 a=x^2-1 a=x2−1, λ 1 = x − a \lambda_1=x-\sqrt{a} λ1=x−a, λ —— 2 = x + a \lambda——2=x+\sqrt{a} λ——2=x+a,则有 λ 1 + λ 2 = 2 x \lambda_1+\lambda_2=2x λ1+λ2=2x, λ 1 . λ 2 = 1 \lambda_1.\lambda_2=1 λ1.λ2=1
则 T n ( x ) = ( λ 1 n − 1 − λ 2 n − 1 ) + x . ( λ 1 n − λ 2 n ) λ 2 − λ 1 ( m o d p ) T_n(x)=\frac{(\lambda_1^{n-1}-\lambda_2^{n-1})+x.(\lambda_1^n-\lambda_2^n)}{\lambda_2-\lambda_1}(mod\;p) Tn(x)=λ2−λ1(λ1n−1−λ2n−1)+x.(λ1n−λ2n)(modp)
= λ 1 n + λ 2 n 2 ( m o d p ) \frac{\lambda_1^n+\lambda_2^n}{2}(mod\;p) 2λ1n+λ2n(modp)
假如 ( x + a ) n = c + d a (x+\sqrt{a})^n=c+d\sqrt{a} (x+a)n=c+da,则 ( x − a ) n = c − d a (x-\sqrt{a})^n=c-d\sqrt{a} (x−a)n=c−da,那么 T n ( X ) = c ( m o d P ) T_n(X)=c(mod\;P) Tn(X)=c(modP)
因此求 ( x + a ) n (x+\sqrt{a})^n (x+a)n是关键。
我们需要求解 ( x + a ) n (x+\sqrt{a})^n (x+a)n,然后取整数部分的结果就是 T n = c ( m o d p ) T_n=c(mod\; p) Tn=c(modp)的结果
作者给出的求解方法,应该是模重复平方计算法。但是我按照作者给的算法和流程图的思路进行编程。发现结果是错误的(可能是我没看懂它的流程图)。所以我根据作者的思路(模重复平方计算法)自己设计程序实现了求解 ( x + a ) n (x+\sqrt{a})^n (x+a)n。
实现
我们知道带根号的乘法运算,计算机实现和手算是不一样的,计算机算会开根号取近似值,而我们在这个算法的过程中不需要开根号,开根号后结果是不正确的,所以我们需要自行编程实现带根号的乘法。
例如:
( c + d a ) 2 = c 0 + d 0 a (c+d\sqrt{a})^2=c_0+d_0\sqrt{a} (c+da)2=c0+d0a
其中
c 0 = c 2 + d 2 a c_0=c^2+d^2a c0=c2+d2a
d 0 = 2 c d d_0=2cd d0=2cd
整数部分: c 0 c_0 c0
带根号部分: d 0 a d_0\sqrt{a} d0a
( c + d a ) ( x + a ) = g + h a (c+d\sqrt{a})(x+\sqrt{a})=g+h\sqrt{a} (c+da)(x+a)=g+ha
其中
g = c x + d a g=cx+da g=cx+da
h = c + d x h=c+dx h=c+dx
整数部分: g g g
带根号部分: h a h\sqrt{a} ha
我们不需要将根号拆开,让它保持原样。需要设计两个函数
- 带根号的平方 pow_2()
- 两个不同的根号数 mul()
代码
def pow_2(c,d,a,p):
'''带根式的多项式的平方,不拆根号'''
x=c*c+d*d*a
y=2*c*d
return (x%p,y%p)
def mul(x1,y1,x2,y2,a,p):
'''带根式的乘法,保证不拆根号'''
x=x1*x2+y1*y2*a
y=x1*y2+x2*y1
return (x%p,y%p)
def T(n,x,p):
a=x*x-1
c,d=x,1
e,f=1,0#初始值
j,k=1,0#初始j,k
while n>0:
ep=n&1
n>>=1
if ep:
j,k=mul(e,f,c,d,a,p)
e,f=j,k
c,d=pow_2(c,d,a,p)
return j
测试:
n=155033642076
x=8909654478045
p=431084178421767
调用函数
T(155033642076,8909654478045,431084178421767)
(注:以下耗时是乘以1020后才统计到的结果,一般情况下都是 0.0)
290588719813696
耗时 1.0004043579101563e+17
将结果除以10^20次方后约等于0.001s
算法实现
求ChebyShev多项式的算法采用矩阵特征值法
密钥产生算法
- 产生一个大的随机数P和Q,计算N=P*Q;
- 随机产生一个大整数x,是的x
- 随机产生一个随机数2<=s
- Alice的公开密钥为(x,N,A),密钥为(S,P)
- 随机产生一个随机数2<=s
手工输入数据产生key的代码
def key():
p=int(input('输入p: '))
q=int(input('输入q: '))
N=p*q
x=int(input('输入x(x))
s=int(input('输入s(2))
A=T(s,x,p)
print('公钥\nx: {}\nN: {}\nA: {}\n私钥\ns: {}\np: {}'.format(x,N,A,s,p))
return (x,N,A),(s,p)
测试
输入p: 48487858671441677503
输入q: 34675575173844376547
输入x(x随机生成p,q,s,r产生key的代码
def randomkey():
num=2
delta=0
pq=[]
for i in range(10**64,10**200):
if num<1:
break
if not Miler_Rabin(i+delta):
pq.append(delta+i)
delta=10**5
num-=1
p=pq[0]
q=pq[1]
N=p*q
x=random.randrange(10**5,p)
s=random.randrange(2,p)
A=T(s,x,p)
print('公钥\nx: {}\nN: {}\nA: {}\n私钥\ns: {}\np: {}'.format(x,N,A,s,p))
测试
++++++++++ 操作 ++++++++++
1 密钥生成
2 加密
3 解密
其它 退出
+++++++++++++++++++++++++
操作数:1
y/n 手动输入p,q,x,s (随机生成):
公钥
x: 3701067950663966601843104319385932777411511926725352977597168006
N:100000000000000000000000000000000000000000000000000000000001002040000000000000000000000000000000000000000000000000000000005708379
A: 8604473064581927969822581060545081655745948659068081426786271706
私钥
s: 6855826339596984719498579332803047617235671254685907621123392070
p: 10000000000000000000000000000000000000000000000000000000000000057
加密算法
- 获得Alice的公开密钥(x,N,A);
- 将m看做一个整数并将m分段,使得m属于Zp,0
- 选择一个随机整数2<=r
- 计算B=Tr(x)(mod N)和X=m*Tr(A)(mod N);
- 将密文消息(B,X)传给Alice。
- 选择一个随机整数2<=r
代码
def encrypt():
print('输入公钥','+'*20)
x=int(input('x: '))
N=int(input('N: '))
A=int(input('A: '))
print('输入待加密明文','+'*20)
m=int(input('m: '))
r=random.randrange(2,x)
B=T(r,x,N)
X=m*T(r,A,N)
print('密文(B,X)','*'*20)
print('B: {}\nX: {}'.format(B,X))
解密算法
- 使用密钥P计算C=B(mod P)
- 使用密钥s计算D=Ts©(mod P)
- 计算m=X*D-1(mod P)恢复明文m。
代码
def decrypt():
print('输入密钥')
p=int(input('p: '))
s=int(input('s: '))
print('输入密文')
B=int(input('B: '))
X=int(input('X: '))
C=B%p
D=T(s,C,p)
m=X*invert(D,p)%p
print('解密出明文','+'*20)
print('m:',m)
算法分析
三种求ChebyShev多项式的算法的比较
首先选取小的参数仿真举例,用计算机随机选取一组1组(n,x,P)。如n=155033642076,x=8909654478045,p=431084178421767,通过计算得到$T_n(x)(mod;p)=$290588719813696
在主频为3.00GHz,内存为16G的计算机下计算,
其中直接迭代法用时太长没有跑完程序就主动中断程序了,普通递归所用时间2.062秒,快速递归所用时间 0.012秒,矩阵特征值所用时间0.001秒。
通过上面的例子可以看出,直接迭代法不可用,普通递归法相对于其它两种方法慢的多。而矩阵特征值法所用时间最短。下面只对“普通递归法”,“快速递归法”和“矩阵特征值法”进行比较。固定p值和x值,改变n值,比较这三种方法求 T n ( x ) ( m o d p ) T_n(x)(mod\;p) Tn(x)(modp)值所用的时间。固定p=431084178421767,x=8909654478045, n ∈ [ 1500 0000 0000 , 1700 0000 0000 ] n\in [1500\;0000\;0000,1700\;0000\;0000] n∈[150000000000,170000000000]之间随机取值,用着三种办法计算所得的时间通过matplotlib库进行做图,如下所示

从图上看普通递归法求值比其它两种方法慢得多
而快速递归法和矩阵特征值法时间相近。理论上是矩阵特征值法比快速递归法还要快。
之所以看着差不多。一方面是迭代次数不大,另一方面是硬件比较好,在迭代次数不大的情况下,体现不出来优势。且花费时间与N没有相关性,而是根据迭代次数(n的取值有关)n符合某个特征的话,执行的次数少,自然花费的时间就越少。
时间与迭代次数成正相关。
而迭代次数不仅与N有关,更与N的构成有关
- N的构成简单: N = e x + c y N=e^x+c^y N=ex+cy,N为这种形式时,它的迭代次数相对较少。
- N的构成越复杂,迭代次数越多。花费时间就越多。
但是不可否认的是:
普通递归法最慢,快速递归法相对较快。但是涉及到递归,递归次数上去后,会消耗大量内存。这也是递归的缺点,虽然代码量少,但是会消耗更多的内存。
而特征值法,时间和空间性都比较好。迭代次数与N的二进制位数有关。
改进算法的数值测试
选择不同长度的密钥,加密同一明文m=64784457424784,对改进算法进行测试。
密钥长度为64位
(1) 密钥产生:产生两个随机素数
P=34126644289158652207
Q=27101092457309781619
则N=924869342138211483322346774027542383133
选取大整数x=7646794539055646799,产生一个随机数s=179696390584392503,计算 A = T s ( x ) ( m o d P ) A=T_s(x)(mod\; P) A=Ts(x)(modP)=23618804596014579605 。所以公开密钥为(x,N,A),私密密钥为(s,P)
(2) 加密运算:随机选取整数r=738494658218590538(需要修改encrypt函数中的r,将随机赋值,改为固定值),计算 B = T r ( x ) ( m o d P ) B=T_r(x)(mod\;P) B=Tr(x)(modP)=64098056950971877262922909844434713538
X = m ∗ T r ( A ) ( m o d N ) X=m*T_r(A)(mod\; N) X=m∗Tr(A)(modN)=16047118512433490570593784159857162769332009033172672
密文信息为(B,X)
加密时间为:0.0秒
(3)解密运算:计算 C = B ( m o d P ) C=B(mod\;P) C=B(modP)= , D = T s ( C ) ( m o d P ) D=T_s(C)(mod\;P) D=Ts(C)(modP)=
则 m = X / D ( m o d P ) m=X/D(mod P) m=X/D(modP)= 64784457424784 解出明文
解密时间为 0.0秒(时间太小,最靠近0.0)
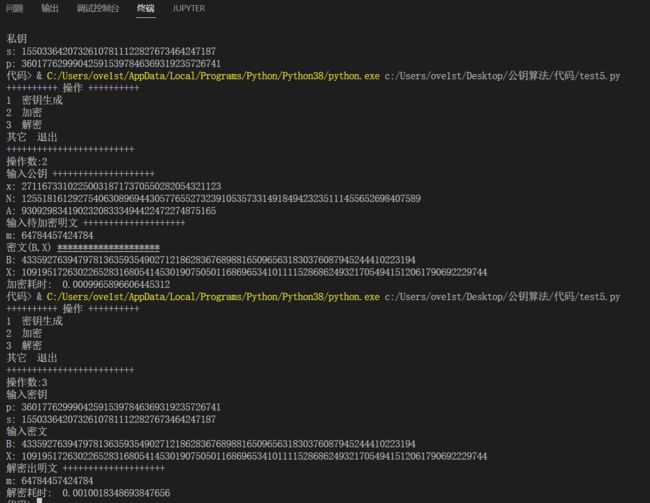
密钥长度为128位
(1) 密钥产生:产生两个随机素数
P=360177629990425915397846369319235726741
Q=348489608574776096131124912618883538129
则N=125518161292754063089694430577655273239105357331491849423235111455652698407589
选取大整数x=271167331022500318717370550282054321123,产生一个随机数s=15503364207326107811122827673464247187,计算 A = T s ( x ) ( m o d P ) A=T_s(x)(mod\; P) A=Ts(x)(modP)= 93092983419023208333494422472274875165。所以公开密钥为(x,N,A),私密密钥为(s,P)
(2) 加密运算:随机悬疑整数r=1144622009756027592,计算 B = T r ( x ) ( m o d P ) B=T_r(x)(mod\;P) B=Tr(x)(modP)=43359276394797813635935490271218628367689881650965631830376087945244410223194
X = m ∗ T r ( A ) ( m o d N ) X=m*T_r(A)(mod\; N) X=m∗Tr(A)(modN)=1091951726302265283168054145301907505011686965341011115286862493217054941512061790692229744
密文信息为(B,X)
加密时间为: 0.0009965896606445312秒
(3)解密运算:计算 C = B ( m o d P ) C=B(mod\;P) C=B(modP)= , D = T s ( C ) ( m o d P ) D=T_s(C)(mod\;P) D=Ts(C)(modP)=
则 m = X / D ( m o d P ) m=X/D(mod P) m=X/D(modP)= 64784457424784 解出明文
解密时间为 0.0010018348693847656秒
论文中的一些错误
数据错误
在计算ChebyShev多项式的值的地方,论文中的有些数据是错误的。
只截取一个示例,这样的错误不只一处

矩阵特征值求Chebyshev多项式的值
我的解决办法
作者给出的求解方法,应该是模重复平方计算法。但是我按照作者给的算法和流程图的思路进行编程。发现结果是错误的(可能是我没看懂它的流程图)。所以我根据作者的思路(模重复平方计算法)自己设计程序实现了求解 ( x + a ) n (x+\sqrt{a})^n (x+a)n。
源代码
完整源代码
链接:https://pan.baidu.com/s/19dbpm1vHSY1jhkP3CLVoAw?pwd=tqcz
提取码:tqcz