机器学习算法基础——逻辑回归

01逻辑回归可以用来解决简单的二分类问题。
逻辑回归的预测函数为$h_{\theta }(x)=g({\theta }^{T}x)$，其中$g(x)$为$sigmoid$函数，用于将数值映射到区间$[0,1]$中，然后再取对数值用于刻画损失函数。

线性逻辑回归：

我们先来实现一个简单的线性逻辑回归的二分类问题：
数据下载：https://pan.baidu.com/s/17bCV1et7fpr2T2XK3dcRRA?pwd=o4br

import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
from sklearn.metrics import classification_report #计算正确率，召回率，F1值
from sklearn import linear_model #导入逻辑回归模型库

data=np.genfromtxt("LR-testSet.csv",delimiter=',') #读取数据
x_data=data[:,:-1] #特征
y_data=data[:,-1]  #标签
column,row=data.shape

x0=[]
y0=[]
x1=[]
y1=[]

def classify(): #分类并绘制散点图
    for i in range(column):
        if(data[i,-1]==1):
            x0.append(x_data[i,0])
            y0.append(x_data[i,1])
        else:
            x1.append(x_data[i,0])
            y1.append(x_data[i,1])
    plt.scatter(x0,y0,c='b',marker='.',label='0')
    plt.scatter(x1,y1,c='r',marker='x',label='1')
classify() 

model=linear_model.LogisticRegression() 
model.fit(x_data,y_data) #建立逻辑回归模型

x_=np.arange(-4,4,0.01)
classify()
y_=-(model.intercept_+model.coef_[0][0]*x_)/model.coef_[0][1]
plt.plot(x_,y_,c='y') #输出分类线
plt.legend()
plt.title("01逻辑回归")
plt.xlabel("x0")
plt.ylabel("x1")
plt.show()

predictions=model.predict(x_data)
print(classification_report(y_data,predictions)) #输出分类结果分析

可以看到正确率在95%左右，效果比较不错。

非线性逻辑回归

我们再来实现一个非线性的逻辑回归：
数据下载：https://pan.baidu.com/s/1D3Rp2XYeB_dXjTR-fj2mYg?pwd=l9vi

import numpy as np
import matplotlib.pyplot as plt
from sklearn import linear_model
from sklearn.metrics import classification_report
from sklearn.preprocessing import PolynomialFeatures #多项式特征库

data=np.genfromtxt("LR-testSet2.txt",delimiter=',') 
x_data=data[:,:-1]
y_data=data[:,-1]
colomn,row=data.shape

x0=[]
y0=[]
x1=[]
y1=[]
def classify():
    for i in range(colomn):
        if(y_data[i]==0):
            x0.append(x_data[i][0])
            y0.append(x_data[i][1])
        else:
            x1.append(x_data[i][0])
            y1.append(x_data[i][1])
    plt.scatter(x0,y0,c='b',marker='o',label='0')
    plt.scatter(x1,y1,c='r',marker='x',label='1')
classify()
plt.legend()
plt.show()

poly=PolynomialFeatures(degree=2) #采用二次多项式
x_poly=poly.fit_transform(x_data)
model=linear_model.LogisticRegression()
model.fit(x_poly,y_data)
x_min,x_max=x_data[:,0].min()-0.3,x_data[:,0].max()+0.3
y_min,y_max=x_data[:,1].min()-0.3,x_data[:,1].max()+0.3

xx,yy=np.meshgrid(np.arange(x_min,x_max,0.01),np.arange(y_min,y_max,0.01))
z=model.predict(poly.fit_transform(np.c_[xx.flatten(),yy.flatten()])) #先展平，在从列方向叠加
z=z.reshape(xx.shape) #把展平后的一维的z重新变为与xxsize相同的二维数组
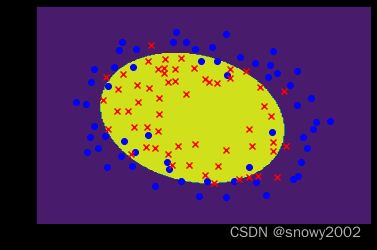
cs=plt.contourf(xx,yy,z) #绘制等高线图
plt.scatter(x0,y0,c='b',marker='o',label='0')
plt.scatter(x1,y1,c='r',marker='x',label='1')
plt.show()

predictions=model.predict(x_poly)
print(classification_report(y_data,predictions))

正确率为81%，也算是相当不错的结果了。