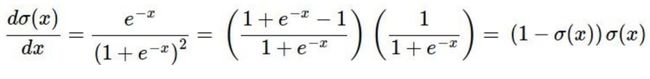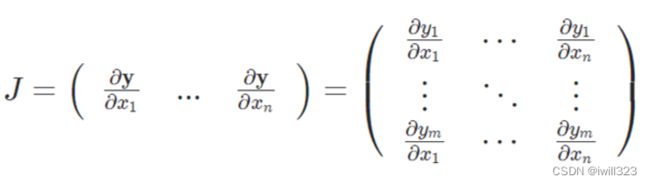CH9 神经网络
超级详细清楚地介绍请先看：神经网络——最易懂最清晰的一篇文章
文章目录
- CH9 神经网络
-
- 9.1 引子
- 9.2 单层神经网络（感知器）
-
- 9.2.1 感知器效果
- 9.3 两层神经网络（多层感知器）
-
- 9.3.1 激活函数
- 9.3.2 一个神经网络前向计算的例子（三层）
- 9.3.3 两层神经网络的训练
- 9.3.3.1 完整的两层神经网络训练实现
- 9.3 反向传播算法
-
- 9.3.1 一个简单的例子
- 9.3.2 反向传播图例
- 9.3.3 反向传播实例：扁平化代码
- 9.3.4 向量的反向传播
- 9.4 神经网络训练
- 9.5 总结
CH9 神经网络
9.1 引子
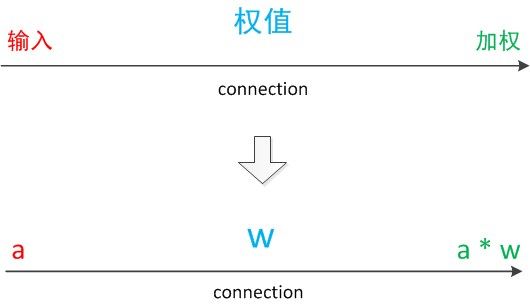
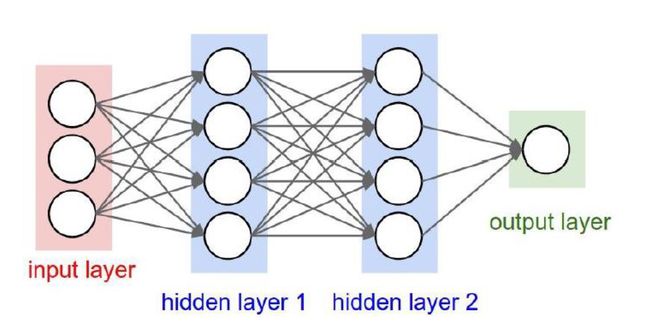
神经元模型，是一个包含输入，输出与计算功能的模型。
下图包含3个输入，1个输出，以及两个计算功能（求和、非线性函数）
注意中间的箭头线，这些线称为“连接”，每个箭头线上有一个“权值”
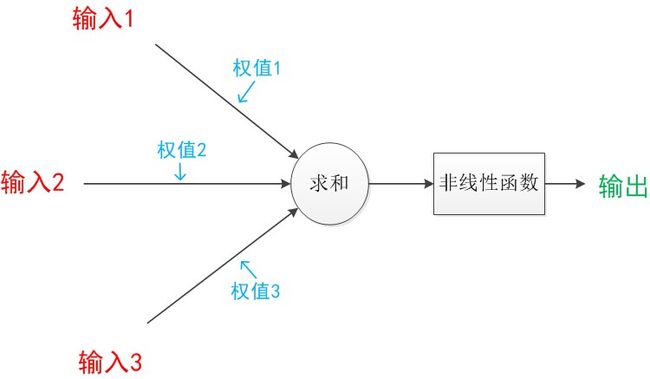
一个神经网络的训练算法就是让权重的值调整到最佳，使得整个网络的预测效果最好
在神经元模型中，每个有向箭头表示的是值的加权传递
将神经元图中的所有变量用符号表示，并写出输出的计算公式，如下图：
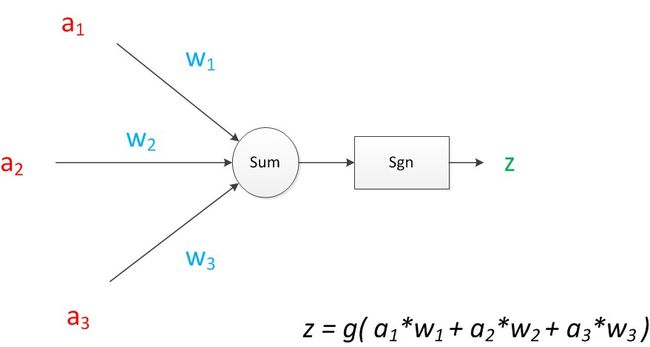
可见z是在输入和权值的线性加权和叠加了一个函数g的值。在MP模型中，函数g是sgn函数，也就是取符号函数，这个函数当输入大于0时，输出1，否则输出0。
一个神经元可以引出多个代表输出的有向箭头，但值都是一样的。
神经元可以看作一个计算与存储单元，计算是神经元对其的输入进行计算功能，存储是神经元会暂存计算结果，并传递到下一层。
理解：
- 一个数据，称之为样本，样本有四个属性，其中三个属性已知，一个属性未知，我们需要做的就是通过三个已知属性预测未知属性
- 具体方法就是使用神经元的公式进行计算，三个已知属性的值是a1，a2，a3，未知属性的值是z，z可以通过公式计算出来
- 在这里，已知的属性称为特征，未知的属性称为目标。假设特征与目标之间确实是线性关系，并且我们已经得到表示这个关系的权值w1，w2，w3，那么我们就可以通过神经元模型预测新样本的目标。
9.2 单层神经网络（感知器）
只能做简单的线性分类任务
两个层次：
- 输入层： 输入单元只负责传输数据，不做计算
- 输出层： 输出单元需要对前一层的输入进行计算
带有两个输入单元的单层神经网络
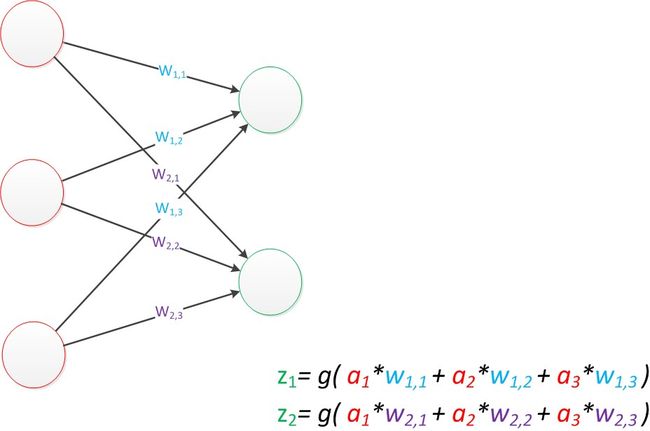
用 w x , y w_{x,y} wx,y来表达一个权值，下标中的x代表后一层神经元序号，y代表前一层神经元序号（序号顺序从上到下）
如果我们仔细看输出的计算公式，会发现这两个公式就是线性代数方程组，因此可以用矩阵乘法来表达这两个公式
输入的变量是 [ a 1 , a 2 , a 3 ] T [a_1,a_2,a_3]^T [a1,a2,a3]T，用向量a表示，方程的左边是 [ z 1 , z 2 ] T [z_1,z_2]^T [z1,z2]T，用向量z表示，系数则是矩阵W（2行3列）。
于是，输出公式可写成g(W * a) = z
9.2.1 感知器效果
与神经元模型不同，感知器中的权值是通过训练得到的。感知器类似一个逻辑回归模型，可以做线性分类任务。
可以用决策分界来形象的表达分类的效果。决策分界就是在二维的数据平面中划出一条直线，当数据的维度是3维的时候，划出一个平面；当数据的维度是n维时，就是划出一个n-1维的超平面
下图显示了在二维平面中划出决策分界的效果，也就是感知器的分类效果
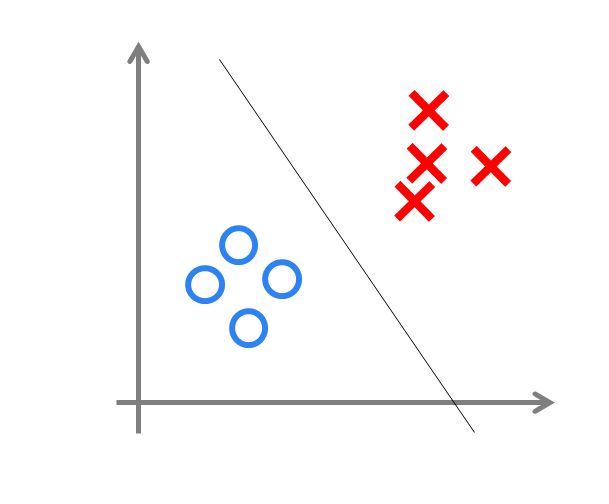
9.3 两层神经网络（多层感知器）
包含输入层，输出层，对比单层神经网络还增加了一个中间层，此时，中间层和输出层都是计算层。
扩展上节的单层神经网络，在右边新加了一个层次（只含一个节点）。
现在权值矩阵增加到了两个，我们用上标来区分不同层次之间的变量。
例如 a x ( y ) a_x^{(y)} ax(y)表示第y层的第x个节点， z 1 z_1 z1， z 2 z_2 z2 变成了 a 1 ( 2 ) a_1^{(2)} a1(2)， a 2 ( 2 ) a_2^{(2)} a2(2)，下图给出了中间层计算
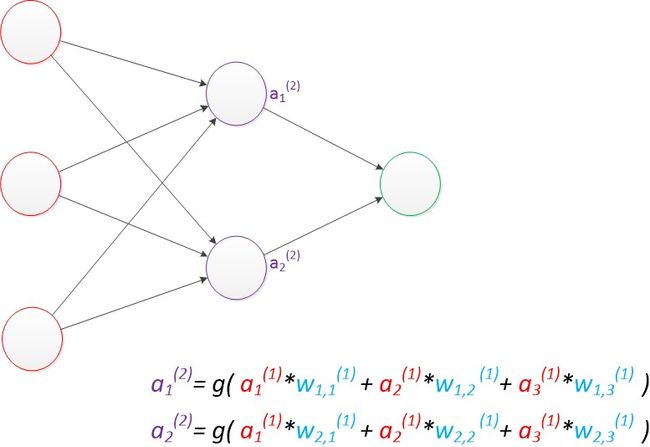
计算最终输出的z时利用了中间层的 a 1 ( 2 ) a_1^{(2)} a1(2) ， a 2 ( 2 ) a_2^{(2)} a2(2)和第二个权值矩阵计算得到，下图为输出层计算
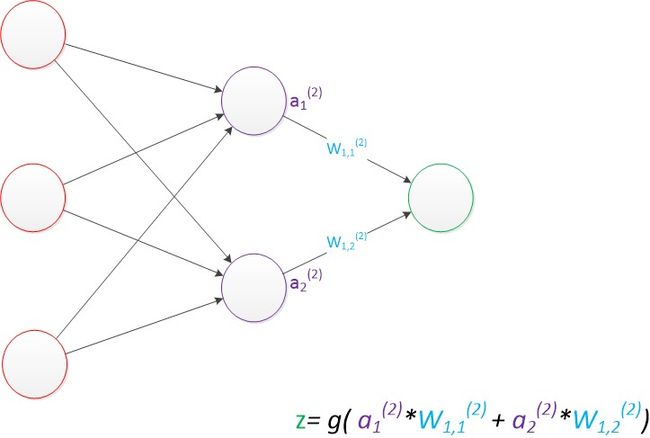
假设我们的预测目标是一个向量，那么与前面类似，只需要在“输出层”增加节点即可。
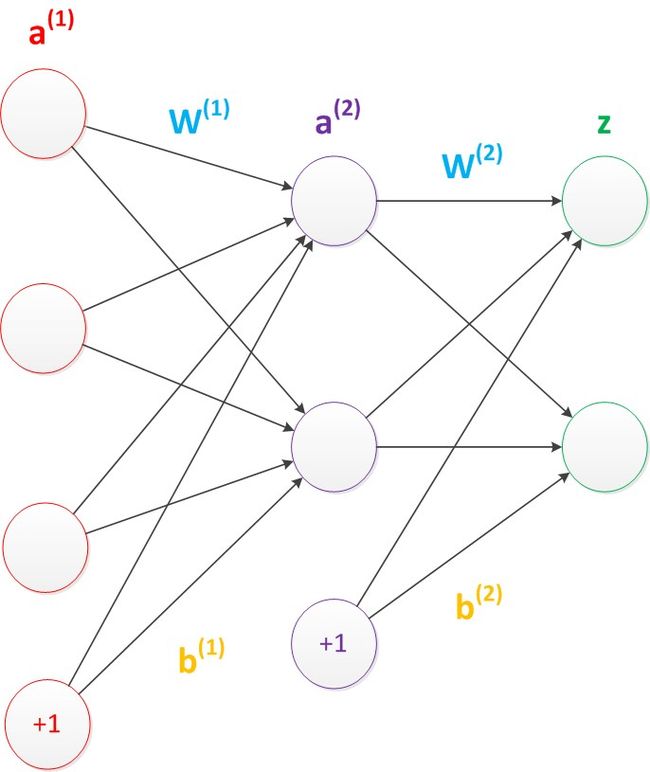
我们使用向量和矩阵来表示层次中的变量。a(1)，a(2)，z是网络中传输的向量数据。W(1)和W(2)是网络的矩阵参数。如下图。
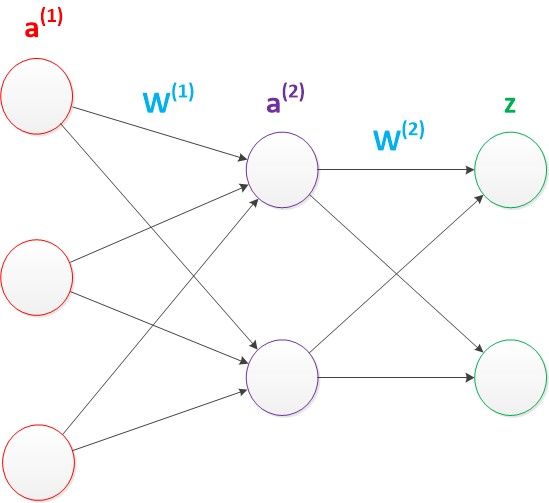
使用矩阵运算来表达整个计算公式如下：
g ( W ( 1 ) ⋅ a ( 1 ) ) = a ( 2 ) g(W^{(1)}\cdot a^{(1)}) = a^{(2)} g(W(1)⋅a(1))=a(2)
g ( W ( 2 ) ⋅ a ( 2 ) ) = z g(W^{(2)}\cdot a^{(2)}) = z g(W(2)⋅a(2))=z
偏置节点：默认存在，本质上是一个只含有存储功能，且存储值永远为1的单元。在神经网络的每个层次中，除了输出层以外，都会含有这样一个偏执单元
前一层没有箭头指向他，一般情况下不会明确画出
考虑了偏置节点以后的神经网络矩阵运算如下：
g ( W ( 1 ) ⋅ a ( 1 ) + b ( 1 ) ) = a ( 2 ) g(W^{(1)}\cdot a^{(1)}+b^{(1)}) = a^{(2)} g(W(1)⋅a(1)+b(1))=a(2)
g ( W ( 2 ) ⋅ a ( 2 ) + b ( 2 ) ) = z g(W^{(2)}\cdot a^{(2)}+b^{(2)}) = z g(W(2)⋅a(2)+b(2))=z
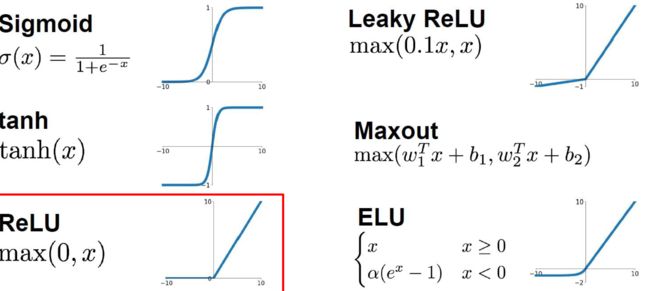
9.3.1 激活函数
即函数g，有以下激活函数我们一般会选择
ReLU对于大多数问题是一个很好的默认选择
9.3.2 一个神经网络前向计算的例子（三层）
（这一部分很有可能我自己的理解是错的，求指正）
f = lambda x: 1.0/(1.0 + np.exp(-x))
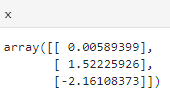
x = np.random.randn(3, 1) # 随机的输入一个向量（3*1）
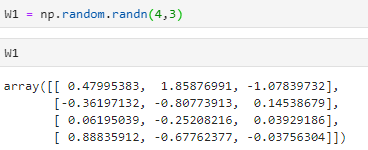
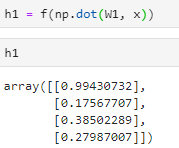
h1 = f(np.dot(W1, x) + b1) # 计算第一层，得到的结果（4*1）
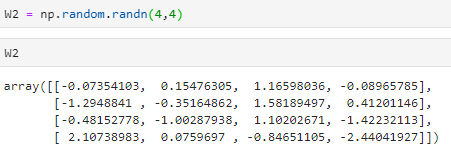
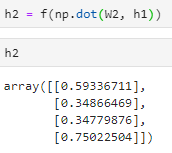
h2 = f(np/dot(W2, h1) + b2) # 计算第二层，得到的结果（4*1）
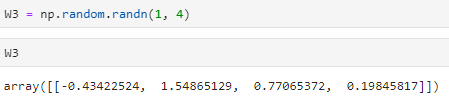
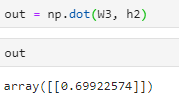
out = np.dot(W3, h2) + b3 # 输出（1*1）
-
f为一个函数，输入的值为x，输出的值为1.0/(1.0 + np.exp(-x))，其中np.exp()返回e的幂次方 -
随机输入一个(3 * 1)的向量，其中
randn(x,y)表示返回由正态分布的随机数组成的x*y的矩阵
-
计算第一层
-
先假设一个W1的值，4个权值，3个输入，所以设4*3
-
计算后得到结果是4 * 1 （4 * 3 · 3 * 1）
-
-
计算第二层
-
假设一个W2的值，4个权值，给4个输入（上一层4个），所以设4*4
-
计算后得到的结果是4 * 1（4 * 4 · 4 * 1）
-
-
输出结果
-
假设一个W3的值，4个权值，给一个输出，所以设1*4
-
计算后得到的结果是1 * 1（1 * 4 · 4 * 1）
-
9.3.3 两层神经网络的训练
首先给所有参数赋上随机值。我们使用这些随机生成的参数值，来预测训练数据中的样本。样本的预测目标为 y p y_p yp，真实目标为y，那么定义一个值loss，计算公式如下：
l o s s = ( y p − y ) 2 loss = (y_p-y)^2 loss=(yp−y)2
这个值称为损失，我们的目标就是使对所有训练数据的损失和尽可能小
9.3.3.1 完整的两层神经网络训练实现
import numpy as np
from numpy.random import randn
网络定义：
N, D_in, H, D_out = 3, 3, 2, 1
x, y = randn(N, D_in), randn(N, D_out)
w1, w2 = randn(D_in, H), randn(H, D_out)
前向计算
for t in range(20):
h = 1 / (1 + np.exp(-x.dot(w1))) # 激活函数
y_pred = h.dot(w2) # 预测值
loss = np.square(y_pred - y).sum() # 损失函数
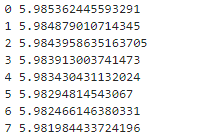
print(t, loss)
其中np.square()表示求矩阵的平方
计算解析梯度
grad_y_pred = 2.0 * (y_pred-y)
grad_w2 = h.T.dot(grad_y_pred)
grad_h = grad_y_pred.dot(w2.T)
grad_w1 = x.T.dot(grad_h * h * (1-h))
梯度下降
w1 -= 1e-4 * grad_w1
w2 -= 1e-4 * grad_w2
反向修改权重
最终结果
形如：
可以看到随着次数的增加损失函数的值是在下降的，这也是我们想要的结果
9.3 反向传播算法
正向传播求损失，反向传播回传误差，同时，神经网络每层的每个神经元都可以根据误差信号修正每层的权重。
如何优化参数，能够让损失函数的值最小
梯度下降算法
梯度下降算法每次计算参数在当前的梯度，然后让参数向着梯度的反方向前进一段距离，不断重复，直到梯度接近零时截止。一般这个时候，所有参数恰好达到使损失函数达到一个最低值的状态
在神经网络模型中，由于结构复杂，每次计算梯度的代价很大，因此还需要使用反向传播算法。
反向传播算法是利用了神经网络的结构进行的计算，不一次计算所有参数的梯度，而是从后往前，首先计算输出层的梯度，然后是第二个参数矩阵的梯度，接着是中间层的梯度，再然后是第一个参数矩阵的梯度，最后是输入层的梯度。计算结束以后，所要的两个参数矩阵的梯度都有了
如下图，梯度的计算从后往前，一层层反向传播。前缀E代表相对导数的意思。
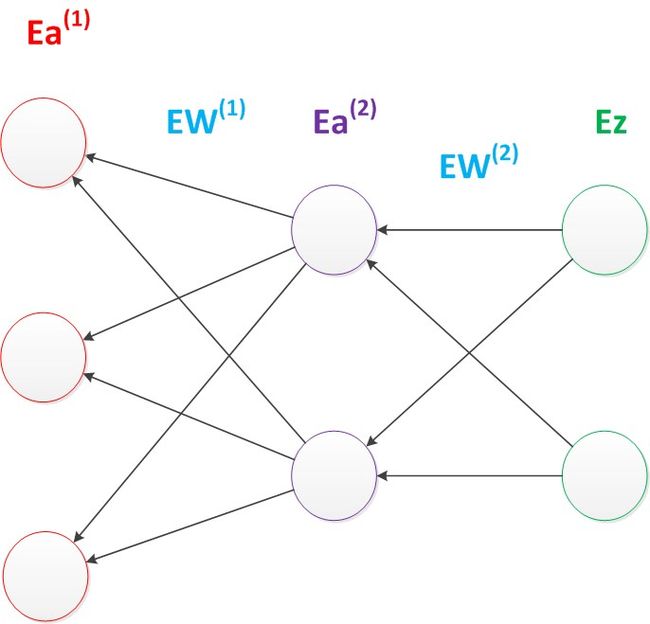
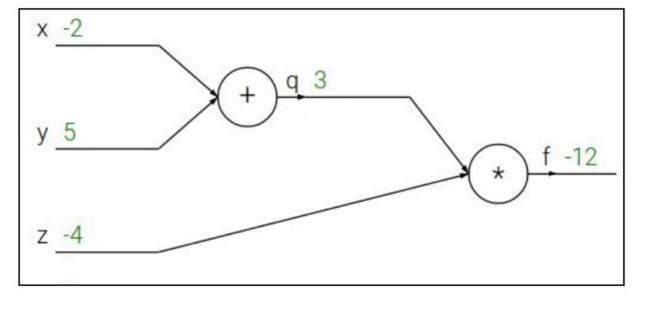
9.3.1 一个简单的例子
下图反应f(x,y,z) = (x+y)z
q = x + y ∂ q ∂ x = 1 , ∂ q ∂ y = 1 q = x+y\quad\frac{\partial q}{\partial x}=1,\frac{\partial q}{\partial y}=1 q=x+y∂x∂q=1,∂y∂q=1
f = q z ∂ f ∂ q = z , ∂ f ∂ z = q f = qz\quad\frac{\partial f}{\partial q} = z,\frac{\partial f}{\partial z}=q f=qz∂q∂f=z,∂z∂f=q
想要得到： ∂ f ∂ x , ∂ f ∂ y , ∂ f ∂ z \frac{\partial f}{\partial x},\frac{\partial f}{\partial y},\frac{\partial f}{\partial z} ∂x∂f,∂y∂f,∂z∂f
通过链式法则：
∂ f ∂ x = ∂ f ∂ q ∂ q ∂ x ∂ f ∂ y = ∂ f ∂ q ∂ q ∂ y \boxed{\frac{\partial f}{\partial x} = \frac{\partial f}{\partial q}\frac{\partial q}{\partial x}}\quad\quad\boxed{\frac{\partial f}{\partial y} = \frac{\partial f}{\partial q}\frac{\partial q}{\partial y}} ∂x∂f=∂q∂f∂x∂q∂y∂f=∂q∂f∂y∂q
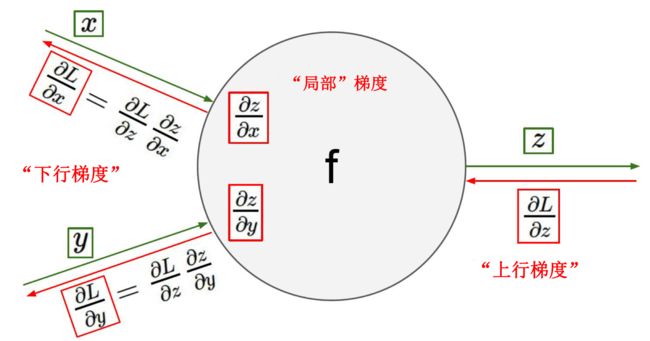
9.3.2 反向传播图例
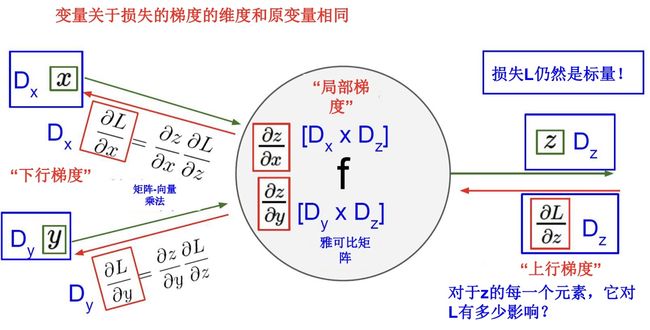
L是z的下一层，可以直接对z求偏导，x和y则要通过z
下行梯度 = 上行梯度 * 局部梯度
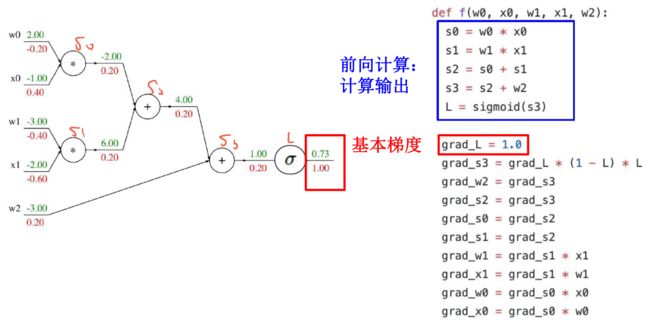
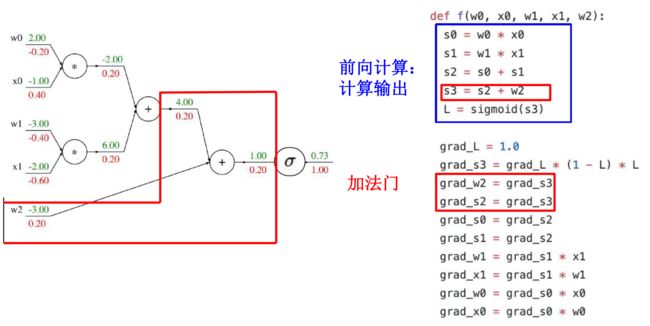
9.3.3 反向传播实例：扁平化代码
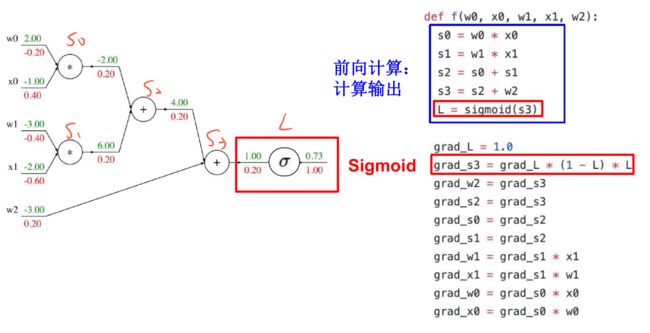
补充：sigmoid局部梯度
再接下去就类似了
9.3.4 向量的反向传播
回顾：向量求导
雅可比矩阵：
由于z是向量，所以局部梯度现在是雅可比矩阵，更新下游梯度的时候采用矩阵乘积
代码：
W = np.random.randn(5, 10)
X = np.random.randn(10, 3)
D = W.dot(X)
dD = np.random.randn(*D.shape) # 与D同样的shape
dW = dD.dot(X.T)
dX = W.T.dot(dD)
9.4 神经网络训练
输入：数据集 { ( x ( i ) , y ( i ) ) } i = 1 n \{(x^{(i)},y^{(i)})\}^n_{i=1} {(x(i),y(i))}i=1n，步长 α \alpha α，小批量大小b，迭代次数T
- 初始化网络参数 w 0 w_0 w0
- for t ∈ { 1 , 2 , ⋯ , T } t\in \{1,2,\cdots,T\} t∈{1,2,⋯,T}
- 从m个样本中均匀随机选取b个样本
- 前向传播逐层计算隐藏层，得到样本输出 y ~ \widetilde{y} y
- 根据损失函数计算误差，计算输出层梯数
- 反向逐层计算隐藏层梯度
- 计算连接参数梯度并更新参数
w t ← w t − 1 − a b ∑ i ∈ m b ∂ w J ( i ) ( w ) w_t \leftarrow w_{t-1}-\frac{a}{b}\sum_{i\in m_b}\partial_wJ^{(i)}(w) wt←wt−1−bai∈mb∑∂wJ(i)(w)
输出：训练收敛的神经网络
9.5 总结
（全连接）神经网络是一系列线性函数和非线性激活函数的堆叠，它们比起线性分类器有更加强大的表示能力
反向传播 = 沿着计算图递归应用链式法则来计算所有输入/参数/中间值的梯度
前向计算：计算运算结果，并将梯度计算所需的任何中间值保存在内存中
反向传播：应用链式法则来计算损失函数相对于输入的梯度