目标运动模型——匀速运动CV
目标运动模型-——匀速运动CV
原创不易,路过的各位大佬请点个赞
WX: ZB823618313
目标运动模型-——匀速运动CV
- 目标运动模型-——匀速运动CV
-
- 1. 目标模型概述
- 2. 目标运动模型
-
- 2.1 匀速运动CV模型
-
- 2.1.1 一维匀速运动CV 模型
- 2.1.2 二维匀速运动CV 模型
- 3.1.1 三维匀速运动CV 模型
- 3.2 匀加速运动CA模型
- 3.3 匀速转弯CT模型
- 3.4 Singer模型
- 3.5 “当前”统计模型
- 3.6 Jerk统计模型
1. 目标模型概述
机动目标模型描述了目标状态随着时间变化的过程。一个好的模型抵得上大量的数据。当前几乎所有的目标跟踪算法都是基于模型进行状态估计的。在卡尔曼滤波器被引入目标跟踪领域后,基于状态空间的机动目标建模成为主要研究对象之一。
目标的空间运动基于不同的运动轨迹和坐标系
一维运动
二维运动
三维运动根据不同方向的运动是否相关
坐标间不耦合模型
坐标间耦合模型
坐标间不耦合模型: 这类模型假设三维空间三个正交方向上的目标机动过程不耦合。目标机动是飞行器受到外力作用而使得加速度变化所致,所以对机动建模的难点在于对目标加速度的描述。对于无机动目标,常速(Constant Velocity,CV〉模型常用于描述这类目标的运动,而常加速度(Constant Acceleration,CA)模型则常用于描述加速度趋近常数的机动目标的运动。
坐标间耦合模型: 坐标间耦合模型绝大多数情况下指的是转弯运动模型。由于此类模型与坐标密切相关,所以可以分为两类:二维转弯模型和三维转弯模型。二维转弯模型又称为平面转弯模型,即CT模型。
下面讲机动目标不同的模型:
2. 目标运动模型
2.1 匀速运动CV模型
匀速运动模型用来匹配目标做匀速直线运动的情况,这也是目标运动最简单的情况.
其中匀速运动模型包括:
一维匀速运动CV 模型
二维匀速运动CV 模型
三维匀速运动CV 模型
2.1.1 一维匀速运动CV 模型
由于目标做匀速直线运动,则目标加速度为0。实际情况中,速度至少要轻微的变化,则加速度常常看做是具有随机特性的扰动输入,可用连续时间的白噪声来建模,并假设其服从均值为零,方差为的高斯分布,即
X ¨ ( t ) = W ( t ) \ddot{X}(t)=W(t) X¨(t)=W(t)
其中 W ( t ) W(t) W(t)零均值白高斯噪声最为普遍。
一维匀速运动模型(连续):
目标状态为:位置和速度、即 X = [ x , x ˙ ] T {X}=[x, \dot{x}]^T X=[x,x˙]T
CV模型为:
X ˙ ( t ) = [ 0 1 0 0 ] X ( t ) + [ 0 1 ] W ( t ) \dot{X}(t)=\begin{bmatrix}0&1\\0&0\end{bmatrix}X(t) + \begin{bmatrix}0\\1\end{bmatrix}W(t) X˙(t)=[0010]X(t)+[01]W(t)
离散化上述模型:
一维匀速运动模型(离散):
X k + 1 = [ 1 T 0 1 ] X k + [ T 2 / 2 T ] W k X_{k+1}=\begin{bmatrix}1&T\\0&1\end{bmatrix}X_{k} + \begin{bmatrix}T^2/2\\T\end{bmatrix}W_k Xk+1=[10T1]Xk+[T2/2T]Wk
T T T为采样时间。
%% 一维匀速CV运动目标轨迹
clc;
clear all;
close all;
n=2; % state dimension : 6
T=1; % sample time.
N=100; %the runs atime,跟踪总时长
w_mu=[0]';
%% target model
q=3; % 目标运动学标准差,过程噪声
Qk=q^2*eye(1);% cov. of process noise
% state matrix
Fk= [1 T
0 T ]; %
Gk= [ T^2/2
T
]; %
%
%% define parameter
sV=zeros(n,N,1,1); % state
x=[1000,20]';
P_0=diag([1e5,10^2]);
x0=mvnrnd(x,P_0); % 初始状态
%x0=(x+normrnd(0,0.001)')';
x=x0';
for k=1:N
%% %%%%%%% target model %%%%%%%%%%%%%%%%%%%%
%% 目标运动学模型(被跟踪目标建模),匀速运动CV模型
w=mvnrnd(w_mu',Qk)';%过程噪声方差
x=Fk*x+Gk*w;
sV(:,k,1,1)=x;
end
% 一维匀速CV运动目标轨迹
ii=1:N;
figure
plot(ii,sV(1,:,1,1),'-*r','LineWidth',1)
grid on
xlabel('时间(s)');ylabel('m');
legend('真实轨迹')
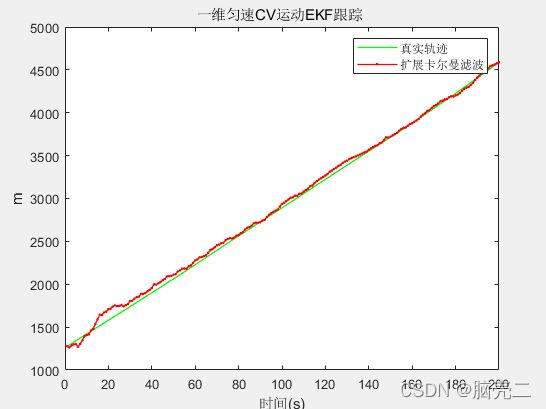
title('一维维匀速运动目标轨迹')
利用扩展卡尔曼滤波EKF跟踪上面的一维匀速运动目标,跟踪轨迹如下
2.1.2 二维匀速运动CV 模型
二维匀速运动模型(连续):
目标状态为:x维位置和速度、y维位置速度、即 X = [ x , x ˙ , y , y ˙ ] T {X}=[x, \dot{x},y, \dot{y}]^T X=[x,x˙,y,y˙]T
CV模型为:
X ˙ ( t ) = [ 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 ] X ( t ) + [ 0 0 1 0 0 0 0 1 ] W ( t ) \dot{X}(t)=\begin{bmatrix}0&1&0&0\\0&0&0&0\\0&0&0&1\\0&0&0&0 \end{bmatrix}X(t) + \begin{bmatrix}0&0\\1&0\\0&0\\0&1\end{bmatrix}W(t) X˙(t)=⎣⎢⎢⎡0000100000000010⎦⎥⎥⎤X(t)+⎣⎢⎢⎡01000001⎦⎥⎥⎤W(t)
离散化上述模型:
二维匀速运动模型(离散):
X k + 1 = [ 1 T 0 0 0 1 0 0 0 0 1 T 0 0 0 1 ] X k + [ T 2 / 2 0 T 0 0 T 2 / 2 0 T ] W k X_{k+1}=\begin{bmatrix}1&T&0&0\\0&1&0&0\\0&0&1&T\\0&0&0&1 \end{bmatrix}X_{k} + \begin{bmatrix}T^2/2&0\\T&0\\0&T^2/2\\0&T\end{bmatrix}W_k Xk+1=⎣⎢⎢⎡1000T100001000T1⎦⎥⎥⎤Xk+⎣⎢⎢⎡T2/2T0000T2/2T⎦⎥⎥⎤Wk
%% 二维匀速CV运动目标轨迹
clc;
clear all;
close all;
n=4; % state dimension : 6
T=1; % sample time.
N=100; %the runs atime,跟踪总时长
w_mu=[0,0]';
%% target model
q=0.1; % 目标运动学标准差,过程噪声
Qk=q^2*eye(2);% cov. of process noise
% state matrix
Fk= [1 T 0 0
0 T 0 0
0 0 1 T
0 0 0 T]; %
Gk= [ T^2/2 0
T 0
0 T^2/2
0 T ]; %
%
%% define parameter
sV=zeros(n,N,1,1); % state
x=[1000,20,1000,20]';
P_0=diag([1e5,10^2,1e5,10^2]);
x0=mvnrnd(x,P_0); % 初始状态
%x0=(x+normrnd(0,0.001)')';
x=x0';
for k=1:N
%% %%%%%%% target model %%%%%%%%%%%%%%%%%%%%
%% 目标运动学模型(被跟踪目标建模),匀速运动CV模型
w=mvnrnd(w_mu',Qk)';%过程噪声方差
x=Fk*x+Gk*w;
sV(:,k,1,1)=x;
end
% 二维匀速CV运动目标轨迹
figure
plot(sV(1,:,1,1),sV(3,:,1,1),'-*r','LineWidth',1)
grid on
xlabel('m');ylabel('m');
legend('真实轨迹')
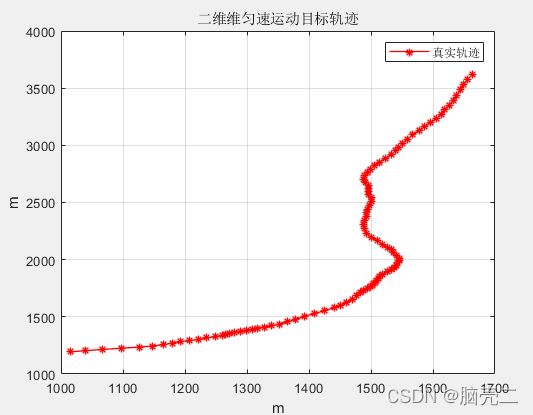
title('二维维匀速运动目标轨迹')
%% 二维匀速CV运动目标轨迹
clc;
clear all;
close all;
n=4; % state dimension : 6
T=1; % sample time.
N=100; %the runs atime,跟踪总时长
w_mu=[0,0]';
%% target model
q=3; % 目标运动学标准差,过程噪声
Qk=q^2*eye(2);% cov. of process noise
% state matrix
Fk= [1 T 0 0
0 T 0 0
0 0 1 T
0 0 0 T]; %
Gk= [ T^2/2 0
T 0
0 T^2/2
0 T ]; %
%
%% define parameter
sV=zeros(n,N,1,1); % state
x=[1000,20,1000,20]';
P_0=diag([1e5,10^2,1e5,10^2]);
x0=mvnrnd(x,P_0); % 初始状态
%x0=(x+normrnd(0,0.001)')';
x=x0';
for k=1:N
%% %%%%%%% target model %%%%%%%%%%%%%%%%%%%%
%% 目标运动学模型(被跟踪目标建模),匀速运动CV模型
w=mvnrnd(w_mu',Qk)';%过程噪声方差
x=Fk*x+Gk*w;
sV(:,k,1,1)=x;
end
% 二维匀速CV运动目标轨迹
figure
plot(sV(1,:,1,1),sV(3,:,1,1),'-*r','LineWidth',1)
grid on
xlabel('m');ylabel('m');
legend('真实轨迹')
title('二维维匀速运动目标轨迹')
利用扩展卡尔曼滤波EKF跟踪上面的二维匀速运动目标,跟踪轨迹如下
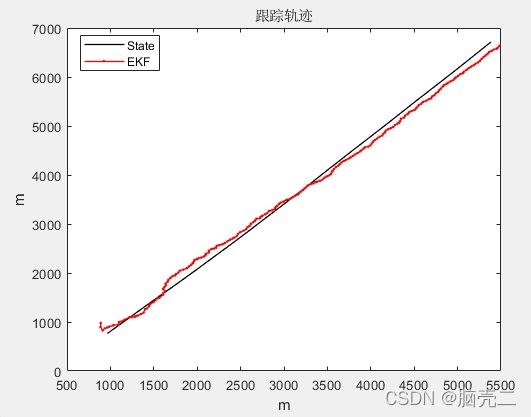
3.1.1 三维匀速运动CV 模型
三维匀速运动CV 模型见另一个博客
3.2 匀加速运动CA模型
匀加速运动CA模型见另一个博客
3.3 匀速转弯CT模型
匀速转弯CT运动模型见另一个博客:包括二维、三维
3.4 Singer模型
Singer模型见另一个博客
3.5 “当前”统计模型
当前统计模型见另一个博客
3.6 Jerk统计模型
Jerk模型见另一个博客
原创不易,路过的各位大佬请点个赞