SHAP：解释模型预测的通用方法

本篇内容来自"A Unified Approach to Interpreting Model Predictions"；

在许多应用中，理解一个模型为什么要进行某种预测与预测的准确性同样重要。然而，现代大型数据集的最高精度往往是通过复杂的模型来实现的，即使是专家也很难解释，比如集成或深度学习模型，这就造成了准确性和可解释性之间的紧张关系。因此，最近提出了各种方法来帮助用户解释复杂模型的预测，但这些方法之间的关系以及一种方法什么时候比另一种方法更好往往是不清楚的。为了解决这个问题，我们提出了一个统一的框架来解释预测，SHAP (SHapley Additive explanation)。SHAP为每个特征分配一个特定预测的重要性值。它的新颖之处包括:

• 确定了一类新的可加性特征重要性测度；
• 理论结果表明，在这类测度中存在一个具有一组理想性质的唯一解。这个新类统一了6个现有的方法，值得注意的是，这个类中最近出现的几个方法都缺乏本文提出的所需属性。

基于这种统一的见解，我们提出了比以前的方法更好的计算性能与人类直觉的一致性的新方法。

引言

正确解释预测模型输出的能力是极其重要的。它能够建立使用者的信任，提供对模型如何改进的见解，并支持对建模过程的理解。在某些应用中，简单模型(例如线性模型)往往因其易于解释而受到青睐，即使它们可能不如复杂模型准确。然而，随着大数据可用性的不断增加，使用复杂模型的好处也越来越多，因此，在模型输出的准确性和可解释性之间进行权衡就成了当务之急。最近人们提出了各种不同的方法来解决这个问题。但是，对于这些方法之间的关系以及哪种方法比哪种方法更好的理解仍然缺乏。

在这里，我们提出了一个新的统一的方法来解释模型的预测。我们的方法导致了三个潜在的令人惊讶的结果，使越来越多的方法变得清晰起来:

• 我们引入了这样一种观点，即把对模型预测的任何解释看作模型本身，我们称之为解释模型（Explanation model）。这让我们可以定义附加特性属性方法的类，它统一了6个当前的方法。
• 然后，我们展示了保证唯一解的博弈论结果适用于整个类别的加性特征属性方法，并提出了SHAP值作为特征重要性的统一度量，各种方法都近似于SHAP值。
• 我们提出了新的SHAP值估计方法，并证明了它们比现有的几种方法更符合使用者研究所衡量的人类直觉，并更有效地区分模型输出类。

Additive Feature Attribution Methods加性特征归因法

对简单模型最好的解释是模型本身。对于复杂模型，如集成方法或深度网络，我们不能使用原始模型作为自己的最佳解释，因为它不容易理解。相反，我们必须使用一个更简单的解释模型，我们将其定义为原始模型的任何可解释的近似。下面我们可以看出，文献中目前的六种解释方法都使用相同的解释模型。这种以前未被重视的统一形式具有有趣的含义，我们将在后面描述。

设$f$为待解释的原始预测模型，$g$为解释模型Explanation model。这里，我们着重于局部方法，这些方法被设计用来解释基于单个输入$x$的预测$f(x)$，如LIME所提到。Explanation model经常使用简化的输入$x^{\prime }$，通过映射函数$x=h_x(x^{\prime })$映射回到原始输入。局部方法在$z^{\prime }\approx x^{\prime }$时尽量确保$g(z^{\prime })\approx f(h_x(x^{\prime }))$。

注意$h_x(x^{\prime })=x$，尽管$x^{\prime }$包含的信息可能比$x$少，因为$h_x$是特定于当前输入$x$的。

定义1：加性特征归因方法的解释模型是二元变量的线性函数$$g(z^{\prime })={\varphi }_0+\sum _{i=1}^M{\varphi }_i{z}_i^{\prime }$$其中，$z^{\prime }\in {\left\{0,1\right\}}^M$，$M$为简化输入特征$x^{\prime }$的维度数量，另外${\varphi }_i\in R$。

解释模型对每个特征属性的影响${\varphi }_i$排序，并将所有特征属性的影响相加，逼近原始模型的输出$f(x)$。许多当前的方法都可以归类对应到定义1。下面讨论其中几个解释方法。

LIME

LIME方法解释个别模型的预测，基于局部逼近模型周围的一个给定的预测。LIME使用的局部线性解释模型完全符合定义1，是一种加性特征归因方法。LIME将简化的输入$x^{\prime }$称为"可解释输入interpretable inputs"，映射$x=h_x(x^{\prime })$将可解释输入的二进制向量转换为原始输入空间。不同类型的$h_x$映射用于不同的输入空间。对于bag of words文本的特征，如果简化输入$x^{\prime }$为1，$h_x$将1或0（存在与否）的向量转换为原始字数；如果简化输入为0，则转换为0。对于图像，$h_x$将图像视为超像素的集合，然后，它将1映射为保留超像素的原始值，将0映射为用相邻像素的平均值替换超像素。

为了找到$\varphi$，LIME将下列目标最小化：$$mi{n}_{g\in G}[L(f,g,{\pi }_{x^{\prime }})+\Omega (g)]$$解释模型$g(z^{\prime })$对原始模型$f(h_x(z^{\prime }))$的信念度（Faithfulness）是通过在简化输入空间中的损失$L$实现的，该简化输入空间由局部核函数${\pi }_{x^{\prime }}$加权得到。$\Omega$用于惩罚$g$的复杂性。

DeepLIFT

DeepLIFT是最近提出的一种用于深度学习的递归预测解释方法。为每个输入$x_i$赋予一个值$C_{\Delta x_i\Delta y}$，表示该输入相对于其原始值被设置为参考值后的效果。这意味着对于DeepLIFT，映射$x=h_x(x^{\prime })$将二进制转换为原始输入，其中1表示输入接受其原始值，0表示接受参考值。参考值虽然是使用者选择的，但代表了改特性的典型非信息背景值。DeepLIFT使用了一个"求和到增量"属性，该属性为：$$\sum _{i=1}^n{C}_{\Delta x_i\Delta o}=\Delta o$$其中，$o=f(x)$是模型的输出，$\Delta o=f(x)-f(r),\Delta x_i=x_i-r_i$，$r$是参考输入。如果我们令${\varphi }_i=C_{\Delta x_i\Delta o}$以及${\varphi }_0=f(r)$，则DeepLIFT可以匹配到定义1。

Layer-Wise Relevance Propagation

分层关联传播方法解释了深度网络的预测。正如Shrikumar等人所指出的，这种方法相当于将所有神经元的参考激活固定为零的DeepLIFT。因此，$x=h_x(x^{\prime })$将二进制值转换为原始输入空间，其中1表示输入原始值，0表示输入0值。

Classic Shapley Value Estimation

之前的三种方法使用合作博弈论的经典方程来计算模型预测的解释：Shapley回归值，Shapley采样值，定量输入影响。

Shapley回归值是存在多重共线性的线性模型的重要特征。该方法需要对所有特征子集$S\subseteq F$重新训练模型，其中$F$是所有特征的集合。Shapley回归值为每个特征赋值，表示包含该特征对模型预测的影响。为了计算这个影响，模型$f_{S\cup \left\{i\right\}}$使用当前特征训练，另一个模型$f_S$使用保留的特征训练。在当前输入下，两个模型的预测被比较$f_{S\cup \left\{i\right\}}(x_{S\cup \left\{i\right\}})-f_S(x_S)$，其中$x_S$代表特征$S$对应的输入。由于保留特征的效果取决于模型中的其他特征 ，因此要对所有可能的子集$S\subseteq F/\left\{i\right\}$计算前面的差异。然后计算Shapley值作为特征属性。它们是所有可能差异的加权平均值：$${\varphi }_i=\sum _{S\subseteq F/\left\{i\right\}}\frac{|S|!(|F|-|S|-1)!}{|F|!}[f_{S\cup \left\{i\right\}}(x_{S\cup \left\{i\right\}})-f_S(x_S)]$$对于Shapley回归值，$h_x$映射1或0到原始输入空间，其中1表示输入包含在模型中，0表示从模型中排除。如果我们令${\varphi }_0=f_{\varnothing }(\varnothing )$，那么Shapley回归值与定义1匹配，因此是一种加性特征归因方法。

Shapley采样值可以用于解释任何模型：

• 对上面公式应用采样逼近；
• 通过对训练数据集的样本进行积分来逼近从模型中移除一个变量的效果。这就消除了对模型进行再训练的需要。

由于Shapley采样值的解释模型形式与Shapley回归值的解释模型形式相同，也是一种加性特征归因方法。

定量输入影响是一个更广泛的框架，解决的不仅仅是特征属性。然而，作为其方法的一部分，它独立地提出了一个近似于Shapley值的采样方法，该方法几乎与Shapley采样值相同。因此，它是另一种加性特征归因方法。

简单属性唯一地决定了可加性特征属性

加法特征属性方法（加性特征归因法）类的一个令人惊讶的属性是该类中存在一个唯一的解决方案，具有三个理想的属性。虽然这些特性对于经典的Shapley值估计方法来说是很常见的，但是对于其他的加性特征属性方法来说，它们是未知的。

属性1：局部精度$$f(x)=g(x^{\prime })={\varphi }_0+\sum _{i=1}^M{\varphi }_i{x}_i^{\prime }$$当$x=h_x(x^{\prime })$时，解释模型$g(x^{\prime })$匹配原始模型$f(x)$，其中${\varphi }_0=f(h_x(\text{0}))$表示关闭所有简化输入时的模型输出。

第二个属性是缺失。如果简化的输入代表特征存在，那么缺失要求原始输入中缺失的特征没有影响。前面描述的所有方法都符合缺失属性。

属性2：缺失$$x_i^{\prime }=0\to {\varphi }_i=0$$缺失限制了$x_i^{\prime }=0$的特征没有属性影响。

第三个属性是一致性。一致性表明，如果模型发生变化，使得某些简化输入的贡献增加或保持不变，而不考虑其他输入，则该输入的属性不应减少。

属性3：一致性

令$f_x(z^{\prime })=f(h_x(z^{\prime }))$并且$z^{\prime }/i$表示设置$z_i^{\prime }=0$。对于任意两个模型$f$和$f^{\prime }$，如果：$$f_x^{\prime }(z^{\prime })-f_x^{\prime }(z^{\prime }/i)\ge f_x(z^{\prime })-f_x(z^{\prime }/i)$$对于所有输入$z^{\prime }\in {\left\{0,1\right\}}^M$，有${\varphi }_i(f^{\prime },x)\ge {\varphi }_i(f,x)$。

定理1：只有一种可能的解释模型遵循定义1并满足属性1、2和3：$${\varphi }_i(f,x)=\sum _{z^{\prime }\subseteq x^{\prime }}\frac{|z^{\prime }|!(M-|z^{\prime }|-1)!}{M!}[f_x(z^{\prime })-f_x(z^{\prime }/i)]$$其中，$|z^{\prime }|$表示$z^{\prime }$中非零项的数量，$z^{\prime }\subseteq x^{\prime }$表示所有的$z^{\prime }$向量，其中非零项是$x^{\prime }$中非零项的子集。

定理1来源于组合合作博弈论的结果，其中的值称为Shapley值。

SHAP values

Shapley值

SHAP值的主要思想就是Shapley值，Shapley值是一个来自合作博弈论（coalitional game theory）的方法，由Shapley在1953年创造的Shapley值是一种根据玩家对总支出的贡献来为玩家分配支出的方法，玩家在联盟中合作并从这种合作中获得一定的收益。用shapley值去解释机器学习的预测，其中“总支出”就是数据集单个实例的模型预测值，“玩家”是实例的特征值，“收益”是该实例的实际预测减去所有实例的平均预测。

假设以下情形：

• 已经训练了一个机器学习模型来预测公寓价格，分别有park、size、floor、cat四个特征。某个面积为50平方米（size=50）、位于二楼（floor=2nd）、附近有一个公园（park=nearby）、禁止猫咪（cat=banned）的公寓，它预测价格为300,000欧元，现在要解释这个预测，即每个特征是如何促进预测的？当所有公寓的平均预测为310,000欧元时，与平均预测相比，每个特征值对预测的贡献是多少？
  线性回归模型的答案很简单，每个特征的贡献是特征的权重乘以特征值，但这仅适用于线性模型，对于更复杂的模型我们需要不同的解决方案，例如LIME建议用局部模型来估计特征的影响，另一种解决方案则来自合作博弈论。
  在公寓示例中，park=nearby，cat=banned，size=50，floor=2nd的特征值共同实现了300,000欧元的预测。我们的目标是解释实际预测（300,000欧元）和平均预测（310,000欧元）之间的差异：-10,000欧元。答案可能是：park=nearby贡献了30,000欧元，size=50贡献了10,000欧元，floor=2nd贡献了0欧元，cat=banned贡献了-50,000欧元，这些贡献加起来为-10,000欧元，即最终预测减去平均预测的公寓价格。

我们感兴趣的是每个特征如何影响预测，在线性模型中很容易计算出各个特征的贡献，以下是一个数据实例的线性模型预测：$$f(x)={\beta }_0+{\beta }_1{x}_1+...+{\beta }_p{x}_p$$其中，$x$是我们想要计算贡献的实例，每个$x_j(j=1,...,p)$是实例的特征值，${\beta }_j$是与特征$j$对应的权重。

定义第$j$个特征对预测$f(x)$的贡献是：$${\varphi }_j={\beta }_j{x}_j-E[{\beta }_j{X}_j]={\beta }_j{x}_j-{\beta }_{j}E[X_j]$$其中$E[{\beta }_j{X}_j]$是特征$j$的平均影响估计，贡献是特征影响与平均影响之间的差异。现在我们知道每个特征对预测的贡献程度了。如果我们将一个实例的所有特征贡献相加，则结果如下：$$\sum _{j=1}^p{\varphi }_j(f)=\sum _{j=1}^p({\beta }_j{x}_j-E[{\beta }_j{X}_j])=({\beta }_0+\sum _{j=1}^p{\beta }_j{X}_j)-({\beta }_0+\sum _{j=1}^{p}E[{\beta }_j{X}_j])=f(x)-E[f(X)]$$也就是说数据点 $x$ 的贡献之和等于预测值减去平均预测值。由于我们在其他非线性模型（比如集成模型）中没有类似的权重，因此我们需要一个不同的解决方案，通过合作博弈论中的Shapley去得到机器学习模型的单个实例预测的特征贡献。

每个特征值的Shapley值是该特征值对预测的贡献，通过对所有可能的特征值组合进行加权和求和得到：$${\varphi }_j(val)=\sum _{S\subseteq \left\{x_1,...,x_p\right\}/\left\{x_j\right\}}\frac{|S|!(p-|S|-1)!}{p!}(val(S\cup \left\{x_j\right\})-val(S))$$其中$S$是模型中使用的特征子集（联盟），$x$是待解释的实例，$p$为特征数量，其中，$\frac{|S|!(p-|S|-1)!}{p!}$是子集$S$的权重。$val(S)$是子集$S$的预测。

---

关于子集权重的理解：
其中，{$x_1,...,x_p$}是所有输入特征的集合，$p$为所有输入特征的数目；$\left\{x_1,...,x_p\right\}/\left\{x_j\right\}$为不包括$\left\{x_j\right\}$的所有输入特征的可能集合，$val(S)$为特征子集$S$的预测；

• 对于分母：$p$个特征在任意排序的情况下有$p!$种组合情况；
• 对于分子：在确定子集$S$后，$p$个特征在特定排序的情况下有$|S|!(p-|S|-1)!$种组合情况。确定子集$S$后，特征的集合为$\left\{x_1,...,x_{|S|},x_j,x_{|S|+2},...,x_p\right\}$，子集$S\left\{x_1,...,x_{|S|}\right\}$本身有$|S|!$种组合，后面紧跟着特征$j$，剩余的特征$\left\{x_{|S|+2},...,x_p\right\}$则有$(p-|S|-1)!$种组合，因此确定子集$S$后共有$|S|!(p-|S|-1)!$种组合；

---

通过上述方式计算Shapley值是不现实的，当特征很多时，计算会很耗费时间。于是提出基于蒙特卡洛采样的近似估计（Shapley采样值）

---

输入：迭代次数$M$，关注的实例 $x$，特征索引 $j$，数据矩阵 $X$ 和机器学习模型 $f$
输出：实例 $x$ 的第 $j$ 个特征值的Shapley值
对于所有的 $m=1,...,M$：

• 从数据矩阵$X$随机抽取实例$z$；
• 生成特征的随机序列$o$；
• 随机顺序实例$x_o=(x_{(1)},...,x_{(p)}),z_o=(z_{(1)},...,z_{(p)})$；
• 构造两个新的实例，有特征$j$：$$x_{+j}=(x_{(1)},...,x_{(j-1)},x_{(j)},z_{(j+1)},...,z_{(p)})$$没有特征$j$：$$x_{-j}=(x_{(1)},...,x_{(j-1)},z_{(j)},z_{(j+1)},...,z_{(p)})$$
• 计算边际贡献：$${\varphi }_j^m=f(x_{+j})-f(x_{-j})$$

最后平均即为Shapley值：$${\varphi }_j=\frac{1}{M}\sum _{m=1}^M{\varphi }_j^m$$

---

上面是Shapley采样值，SHAP值是Shapley值的另一种估计方法

SHAP值

目前许多解释机器学习模型局部预测的方法都属于可加特征归因方法（Additive feature attribution methods），比如LIME、DeepLIFT、 分层相关传播（layer-wise relevance propagation）、Shapley回归值（Shapley regression values），Shapley采样值（Shapley sampling values）和定量输入影响（Quantitative Input Influence），而SHAP（Shapley Additive exPlanations）则是统一了上面六种方法的解释预测框架。

为了计算SHAP值，我们定义$f_x(S)=E[f(x)|x_S]$，其中$S$是输入特征可能的子集（Shapley中的联盟），$E[f(x)|x_S]$是输入特征的子集$S$的条件期望值（Shapley中的$val$函数）。

下图为预测的解释：

可以看出，SHAP值将每个特征的归因值赋值为在调整该特征时模型预测的预期变化，将模型$f$对于样本{$x_1=a_1,x_2=a_2,x_3=a_3,x_4=a_4$}的预测解释为引入条件期望的每个特征的影响${\varphi }_j$的总和。此图只显示了单个排序的情况，上图的解释过程为：

• 首先，$S$为空集时，${\varphi }_0=f_x(\varnothing )=E[f(x)]$，其中，$E[f(x)]$为模型预测值的期望，可用训练样本的模型预测值的平均值近似；
• 接下来$S$顺序加入特征$x_1$，此时${\varphi }_1=f_x(\left\{x_1\right\})-f_x(\varnothing )=E[f(x)|x_1]-E[f(x)]$，即{$x_1=a_1$}时的模型预测期望$-$模型预测期望；
• 然后$S$顺序加入特征$x_2$，此时${\varphi }_2=f_x(\left\{x_1,x_2\right\})-f_x(\left\{x_1\right\})=E[f(x)|x_1,x_2]-E[f(x)|x_1]$，即{$x_1=a_1,x_2=a_2$}时的模型预测期望$-${$x_1=a_1$}时的模型预测期望；
• …
• 直至加入最后一个特征$x_4$，此时${\varphi }_4=f_x(\left\{x_1,x_2,x_3,x_4\right\})-f_x(\left\{x_1,x_2,x_3\right\})=E[f(x)|x_1,x_2,x_3,x_4]-E[f(x)|x_1,x_2,x_3]$，即{$x_1=a_1,x_2=a_2,x_3=a_3,x_4=a_4$}时的模型预测期望$-${$x_1=a_1,x_2=a_2,x_3=a_3$}时的模型预测期望；此时​为四个特征单一排序下的预测值，其实就是样本​的预测值​。

另一个解释实例的规则和上面所述类似：

其他概念

预测值的可视化

假设用100棵树随机训练一个森林分类器来预测宫颈癌的风险，我们将使用SHAP来解释单个样本的预测。Python的shap包带来了一种可视化：可以将Shapley值等特性属性可视化为“力”，每个特征值都是一个增加或减少预测的力。预测从基线开始，基线是所有预测的平均值，每个Shapley值是一个箭头，增加（正值）或减少（负值）预测。

下图显示了来自宫颈癌数据集的两个妇女的SHAP解释力图：

SHAP值是这样解释两个实例的癌症预测概率的：基线为平均预测概率0.066，第一个妇女的预测概率为0.06，有性病（STDs=1）是风险增加的影响，年龄42岁（Age=42）是减少的影响。第二位女性的预测风险为0.71，年龄51岁（Age=51）和吸了34年烟（Smokes…years.=34）增加了她患癌症的风险。

这些都是单个实例预测的解释，Shapley值可以组合成全局解释。如果我们对每个实例运行SHAP，就会得到一个Shapley值的矩阵，这个矩阵每个数据实例有一行，每个特征有一列，可以通过分析这个矩阵中的Shapley值来解释整个模型。

SHAP特征重要度

具有较大Shapley绝对值的特征很重要。由于我们需要全局重要度，因此我们在数据中对每个特征的Shapley绝对值取平均值：$$I_j=\sum _{i=1}^n|{\varphi }_j^{(i)}|$$接下来，我们对特征重要度降序排序并绘制它们，下图显示了SHAP对于之前预测宫颈癌的经过训练的随机森林的特征重要性。

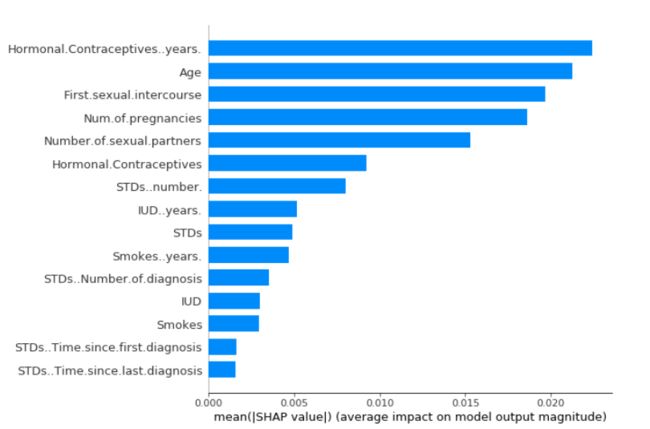
使用激素类避孕药的年数（Hormonal.Contraceptives…years.）是最重要的特征，平均将预测的癌症绝对概率改变了2.4个百分点。

SHAP摘要图

摘要图结合了特征重要度和特征的影响。摘要图上的每个点都是一个特征和一个实例的Shapley值，y轴上的位置由特征决定，x轴上的位置由Shapley值决定，颜色代表特征值从小到大，重叠点在y轴方向上抖动，因此我们可以了解每个特征的Shapley值的分布。

SHAP摘要图显示服用激素避孕药的年数（Hormonal.Contraceptives…years.）越少，患癌症的风险越低，服用年数越多，患癌症的风险越高。不过所有的影响都只是描述了模型的行为，在现实世界中不一定是因果关系。

SHAP依赖图

SHAP依赖图可能是最简单的全局解释图：

• 选择一个特征；
• 对于每个数据实例，绘制一个点，x轴上是特征值，y轴上是对应的Shapley值；

下图显示了服用激素避孕药的年数（Hormonal.Contraceptives…years.）的SHAP依赖图，该图包含所有的点${\left\{(x_j^{(i)},{\varphi }_j^{(i)})\right\}}_{i=1}^n$：

可以看到，与0年相比，服用激素避孕药的年数少则预测概率低，年数多则预测癌症概率高。