Python通过机器学习实现对个人信用评估
资源下载地址:https://download.csdn.net/download/sheziqiong/85884404
资源下载地址:https://download.csdn.net/download/sheziqiong/85884404
一、项目介绍
在银行贷款行为中,银行最关心的就是贷款人是否会违约从而造成贷款损失。而避免贷款被发放给可能违约的贷款人的主要手段就是对贷款人进行信用评估。
信用评估是银行对借款人信用情况进行评估的一种活动。银行贷款的最基本条件是信用,信用好就容易取得银行贷款支持,信用差就难以取得银行贷款支持。而借款人信用是由多种因素构成的,包括借款人资产负债状况、经营管理水平、产品经济效益及市场发展趋势等等。为了对借款人信用状况有一个统一的基本的正确的估价,以便正确掌握银行贷款,就必须对借款人信用状况进行评估。
1.信用评估介绍
信用评估包括个人信用评分、企业信用评级和职业信用评价等。其中个人信用评分指信用评估机构利用信用评分模型对消费者个人信用信息进行量化分析,以分值形式表述。除此之外,还有个人综合信用评分,指通过使用科学严谨的分析方法,综合考察影响个人及其家庭的内在和外在的主客观环境,并对其履行各种经济承诺的能力进行全面的判断和评估。
一般针对个人信用评分时,会主要参考诸如个人基本信息、银行信用信息、个人缴费信息、个人资本状况四类变量,其中,银行信用信息所占权重最大,接近50%,其余三类变量所占权重大致相当。
2. 数据集来源
数据集选自阿里天池贷款违约预测比赛数据集。赛题以预测用户贷款是否违约为任务,数据集报名后可见并可下载,该数据来自某信贷平台的贷款记录,总数据量超过120w,包含47列变量信息,其中15列为匿名变量。为了保证比赛的公平性,将会从中抽取80万条作为训练集,20万条作为测试集A,20万条作为测试集B,同时会对employmentTitle、purpose、postCode和title等信息进行脱敏。
二、数据处理
1. 数据集各项特征含义
| 特征名 | 含义 |
|---|---|
| id | 为贷款清单分配的唯一信用证标识 |
| loanAmnt | 贷款金额 |
| term | 贷款期限(year) |
| interestRate | 贷款利率 |
| installment | 分期付款金额 |
| grade | 贷款等级 |
| subGrade | 贷款等级之子级 |
| employmentTitle | 就业职称 |
| employmentLength | 就业年限(年) |
| homeOwnership | 借款人在登记时提供的房屋所有权状况 |
| annualIncome | 年收入 |
| verificationStatus | 验证状态 |
| issueDate | 贷款发放的月份 |
| purpose | 借款人在贷款申请时的贷款用途类别 |
| postCode | 借款人在贷款申请中提供的邮政编码的前3位数字 |
| regionCode | 地区编码 |
| dti | 债务收入比 |
| delinquency_2years | 借款人过去2年信用档案中逾期30天以上的违约事件数 |
| ficoRangeLow | 借款人在贷款发放时的fico所属的下限范围 |
| ficoRangeHigh | 借款人在贷款发放时的fico所属的上限范围 |
| openAcc | 借款人信用档案中未结信用额度的数量 |
| pubRec | 贬损公共记录的数量 |
| pubRecBankruptcies | 公开记录清除的数量 |
| revolBal | 信贷周转余额合计 |
| revolUtil | 循环额度利用率,或借款人使用的相对所有可用循环信贷的信贷金额 |
| totalAcc | 借款人信用档案中当前的信用额度总数 |
| initialListStatus | 贷款的初始列表状态 |
| applicationType | 表明贷款是个人申请还是与两个共同借款人的联合申请 |
| earliesCreditLine | 借款人最早报告的信用额度开立的月份 |
| title | 借款人提供的贷款名称 |
| policyCode | 公开可用的策略_代码=1新产品不公开可用的策略_代码=2 |
| n系列匿名特征 | 匿名特征n0-n14,为一些贷款人行为计数特征的处理 |
2. 数据缺失项处理
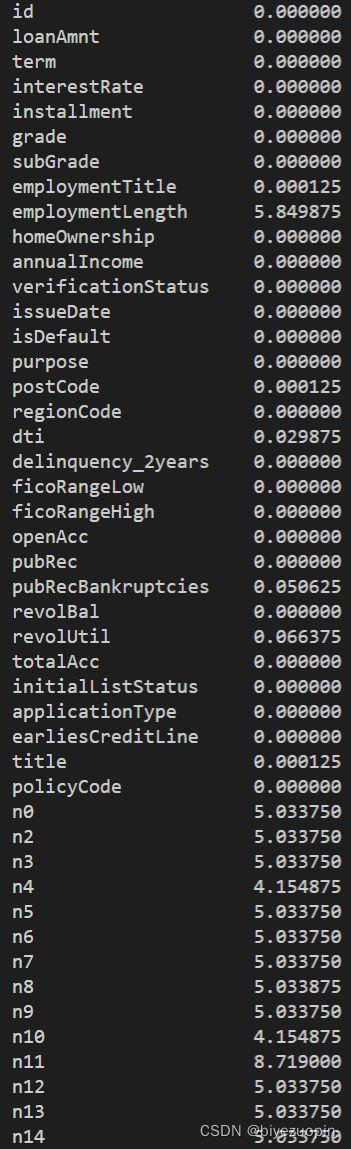
检查数据集中是否存在部分特征有缺失的情况,代码与效果如下:
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
def collect_na_value(dataframe):
return dataframe.isna().sum() / dataframe.shape[0] * 100
if __name__ == "__main__" :
### 读取数据 ###
data = pd.read_csv("..\\dataset\\raw\\train.csv", index_col = 'id')
### 读取缺失项 ###
null_info = collect_na_value(data)
### 可视化 ###
plt.figure()
plt.plot(null_info)
plt.show()
原数据集中有特征存在缺失项,但是确实项比例占比均不超过10%,因此不用废弃特征。但仍需要对缺失的数据进行填充。其中需要区分数据中的连续数值型数据、离散数值型数据以及对象类型数据(即数据内容为字符串等),代码如下:
# 读入数据
self.data = pd.read_csv(dataPath, index_col = 'id')
### 数值型数据分类 ###
#数值类型: numerical_feature
self.numerical_feature = list(self.data.select_dtypes(exclude=['object']).columns)
#对象类型: category_feature: ['grade', 'subGrade', 'employmentLength', 'issueDate', 'earliesCreditLine']
self.category_feature = list(filter(lambda x: x not in self.numerical_feature,list(self.data.columns)))
# 遍历判断数值型变量是连续还是离散(以变化类型是否超过15为界限)
for feature in self.numerical_feature:
temp = self.data[feature].nunique()
if temp <= 15:
self.discrete_feature.append(feature)
else:
self.serial_feature.append(feature)
在分类完成后,将数值型特征缺失项用中位数填充;而对象类型适用众数填充
# 数值型用中位数填充
for col in self.numerical_feature:
self.data[col].fillna(self.data[col].median(), inplace = True )
# 对象型用众数填充
for col in self.category_feature:
self.data[col].fillna(self.data[col].mode(), inplace = True)
# ['employmentLength']项特殊对待,用上一项进行填充
self.data['employmentLength'].fillna(method='pad', inplace = True)
3. 时间戳特征数据处理
经检查发现,‘issueDate’, 'earliesCreditLine’两类特征为时间戳类型。根据数据含义可知’issueDate’代表贷款发放的月份,'earliesCreditLine’代表借款人最早报告的信用额度开立的月份。通过经验可知,这两个时间戳的差值为报告信用额度开立到贷款发放的用时,这相比这两个特征原先的时间戳数据而言,对贷款者的信用评估影响更大。因此决定将这两个特征做差得到新特征,并在原数据集中进行替换。代码如下:
# 该类型均为年/月/日类型字符串
# 考虑将两者合并,只记录差值,存放于['CreditLine']列中
data_earliesCreditLine_year = self.data['earliesCreditLine'].apply(lambda x:x[-4:]).astype('int64')
data_issueDate_year = self.data['issueDate'].apply(lambda x:x[:4]).astype('int64')
# 将二者做差
self.data['CreditLine'] = data_issueDate_year - data_earliesCreditLine_year
# 丢弃原项
self.data = self.data.drop(['earliesCreditLine','issueDate'], axis=1)
4. 对象型特征编码处理
观察发现’grade’,'subGrade’这两个特征的数据内容为字母与数字的组合,其含义为贷款等级。因此考虑对其进行简单编码,从而将其转换为数值型。代码如下:
### ['grade', 'subGrade']类型 ###
# 这两列是简单的字符、字符串代码,考虑对这两列手动编码
a2z = 'ABCDEFGHIJKLMNOPQRSTUVWXYZ'
a2z_code = np.arange(1,27)
a2z_mapping = dict(zip(a2z, a2z_code))
# 遍历对这两个特征进行替换
self.data.loc[:,['grade','subGrade']] = self.data.loc[:,['grade','subGrade']].applymap(lambda g:g.replace(g[0], str(a2z.index(g[0])+1))).astype('int')
而’employmentLength’这一特征数据内容为字符串类型,其含义为工作年限。因此只用提取字符串中工作年限的数字即可。代码如下:
### ['employmentLength']类型 ###
# 该类型是字符串,种类多样:"<1 year", "n years", "10+ years" 共12种
# 由于种类固定,直接提取其中的数字
self.data['employmentLength'] = self.data['employmentLength'].replace({'< 1 year':'1 year','10+ years':'10 years'}).str.split(' ',expand=True)[0].astype('int64')
5.测试集分割
由于原数据集中测试集不包含违约与否的答案数据。因此本次试验中,我们将训练集的后20万条数据(不含缺失项)分割出,作为测试集。
三、模型选择
1. GBDT
GBDT (Gradient Boosting Decision Tree) 是机器学习中一个长盛不衰的模型,其主要思想是利用弱分类器(决策树)迭代训练以得到最优模型,该模型具有训练效果好、不易过拟合等优点。GBDT不仅在工业界应用广泛,通常被用于多分类、点击率预测、搜索排序等任务;在各种数据挖掘竞赛中也是致命武器,据统计Kaggle上的比赛有一半以上的冠军方案都是基于GBDT。
2. LGBMRegressor
LightGBM(Light Gradient Boosting Machine)是一个实现GBDT算法的框架,支持高效率的并行训练,并且具有更快的训练速度、更低的内存消耗、更好的准确率、支持分布式可以快速处理海量数据等优点。
为了避免上述XGBoost的缺陷,并且能够在不损害准确率的条件下加快GBDT模型的训练速度,lightGBM在传统的GBDT算法上进行了如下优化:
-
基于Histogram的决策树算法。
-
单边梯度采样 Gradient-based One-Side Sampling(GOSS):使用GOSS可以减少大量只具有小梯度的数据实例,这样在计算信息增益的时候只利用剩下的具有高梯度的数据就可以了,相比XGBoost遍历所有特征值节省了不少时间和空间上的开销。
-
互斥特征捆绑 Exclusive Feature Bundling(EFB):使用EFB可以将许多互斥的特征绑定为一个特征,这样达到了降维的目的。
-
带深度限制的Leaf-wise的叶子生长策略:大多数GBDT工具使用低效的按层生长 (level-wise) 的决策树生长策略,因为它不加区分的对待同一层的叶子,带来了很多没必要的开销。实际上很多叶子的分裂增益较低,没必要进行搜索和分裂。LightGBM使用了带有深度限制的按叶子生长 (leaf-wise) 算法。
-
直接支持类别特征(Categorical Feature)
-
支持高效并行
-
Cache命中率优化
3. GridSearchCV
GridSearchCV,它存在的意义就是自动调参,只要把参数输进去,就能给出最优化的结果和参数。但是这个方法适合于小数据集,一旦数据的量级上去了,很难得出结果。这个时候就是需要动脑筋了。数据量比较大的时候可以使用一个快速调优的方法——坐标下降。它其实是一种贪心算法:拿当前对模型影响最大的参数调优,直到最优化;再拿下一个影响最大的参数调优,如此下去,直到所有的参数调整完毕。
四、实验结果分析
1. 第一次试验
第一次试验我们直接将完成了数据处理后的数据传入模型训练。训练结果使用k-Fold进行本地验证,并用auc对测试集进行验证。评价指标如下:
| 本地测试 | 训练集测试 |
|---|---|
| 0.7249421218515957 | 0.7241445091503432 |
2. 第二次试验
第二次试验,我们对各特征值进行优化,希望减少训练集中的无用数据,从而加快后续试验中的训练速度。
1.检查数据分布
首先我们绘制了所有数据的分布图,其中policyCode, annualIncome, applicationType, n11, n12, n13特征数据几乎没有变化,因此将他们从训练集中排除。其分布情况如下图所示:
分析特征间线性关系
首先我们绘制出所有特征的热力图:
图中policyCode, annualIncome, applicationType, n11, n12, n13项的异常是由于其有效数据过少而造成的,由于在上一步中决定删去这些特征,因此此处不再进行讨论。随后我们打印出相关系数较高的服务对:
| feature_x | feature_y | corr |
|---|---|---|
| loanAmnt | installment | 0.9533692932239131 |
| interestRate | grade | 0.9532685750717439 |
| interestRate | subGrade | 0.9708469479718348 |
| grade | subGrade | 0.9939067441072746 |
| ficoRangeLow | ficoRangeHigh | 0.9999999288414679 |
| openAcc | n7 | 0.817523495370809 |
| openAcc | n10 | 0.9838900341270191 |
| n1 | n2 | 0.8081573447236511 |
| n1 | n3 | 0.801243568608452 |
| n1 | n4 | 0.8266510426867069 |
| n1 | n9 | 0.801243568608452 |
| n2 | n3 | 1.0 |
| n2 | n9 | 0.9820448979716367 |
| n3 | n9 | 0.838420270694751 |
| n5 | n8 | 0.838420270694751 |
| n7 | n10 | 0.826807072189599 |
我们将具有高相关性的特征对分布图绘制出来进行人工分析:
分析后发现,grade与subgrade特征中,subgrade特征完全包含了grade的信息,因此可以考虑删除grade特征;openAcc-totalAcc-n1-n2-n3-n4-n7-n9,loanAmnt-installment,intersetRate-subGrade这三组特征均存在线性关系,但是不能互相替代,因此考虑使用pca降维的方式处理。
2. pca降维
上一步中发现了具有强相关关系的三组特征[“openAcc”, “totalAcc”, “n1”, “n2”, “n3”, “n4”, “n7”, “n9”], [“loanAmnt”, “installment”], [“interestRate”, “subGrade”]
准备使用pca对这三组数据进行降维处理。其中第二三组均降至一维即可。而对于第一组特征的降维目标参数需要斟酌。
以下是对第一组数据降维后能保留的信息,由下图可知,在仅保留3个维度的特征前提下,仍然能保证整体信息丢失较少。
pca降维代码实现如下:
import pandas as pd
import numpy as np
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
def getNcomponents(train, columns) :
train_col = train.loc[:,columns]
### 可视化寻找n_components最优取值 ###
pca = PCA().fit(train_col) # 默认n_components为特征数目4
pca_info = pca.explained_variance_ratio_
# print("每个特征在原始数据信息占比:\n", pca_info)
pca_info_sum = np.cumsum(pca_info)
# print("前i个特征总共在原始数据信息占比:\n", pca_info_sum)
plt.plot(range(1,len(columns)+1), pca_info_sum) # [1, 2, 3, 4]表示选1个特征、2个特征...
plt.xticks(range(1,len(columns)+1)) # 限制坐标长度
plt.xlabel('The number of features after dimension')
plt.ylabel('The sum of explained_variance_ratio_')
plt.savefig("pca")
plt.show()
if __name__ == "__main__" :
### 读取数据 ###
train = pd.read_csv("..\\output\\experiment1\\data\\train.csv")
test = pd.read_csv("..\\output\\experiment1\\data\\test.csv")
### 手动降维 ###
# 删去有效信息过少的特征
useless_col = ["policyCode", "annualIncome", "applicationType", "n11", "n12", "n13"]
train.drop(useless_col,axis=1,inplace=True) # axis=0表示行;axis=1表示列
test.drop(useless_col,axis=1,inplace=True) # axis=0表示行;axis=1表示列
# 删去可被替换的特征
replaceable_col = ["grade"]
train.drop(replaceable_col,axis=1,inplace=True)
test.drop(replaceable_col,axis=1,inplace=True)
### pca降维 ###
col_pca_1 = ["openAcc", "totalAcc", "n1", "n2", "n3", "n4", "n7", "n9"]
col_pca_2 = ["loanAmnt", "installment"]
col_pca_3 = ["interestRate", "subGrade"]
train_col_1 = train.loc[:,col_pca_1]
train_col_2 = train.loc[:,col_pca_2]
train_col_3 = train.loc[:,col_pca_3]
test_col_1 = test.loc[:,col_pca_1]
test_col_2 = test.loc[:,col_pca_2]
test_col_3 = test.loc[:,col_pca_3]
### 针对第一组求最佳n_components参数 ###
getNcomponents(train, col_pca_1)
### pca降维:第一组 ###
pca_1 = PCA(n_components=3) # 设置pca参数
# 做归一化等操作后直接使用pca降维(即SVD分解)
train_col_1 = pca_1.fit_transform(train_col_1)
test_col_1 = pca_1.transform(test_col_1)
# 生成存放新特征用的DataFrame数据
train_pca_1 = pd.DataFrame(train_col_1,columns=['pca1-1','pca1-2','pca1-3'])
test_pca_1 = pd.DataFrame(test_col_1,columns=['pca1-1','pca1-2','pca1-3'])
# 删去原有特征
train.drop(col_pca_1,axis=1,inplace=True)
test.drop(col_pca_1,axis=1,inplace=True)
# 添加入新特征至原DataFrame数据
train = pd.concat([train,train_pca_1],axis=1)
test = pd.concat([test,test_pca_1],axis=1)
### pca降维:第二组 ###
pca_2 = PCA(n_components=1)
train_col_2 = pca_2.fit_transform(train_col_2)
test_col_2 = pca_2.transform(test_col_2)
train_pca_2 = pd.DataFrame(train_col_2,columns=['pca2'])
test_pca_2 = pd.DataFrame(test_col_2,columns=['pca2'])
train.drop(col_pca_2,axis=1,inplace=True)
test.drop(col_pca_2,axis=1,inplace=True)
train = pd.concat([train,train_pca_2],axis=1)
test = pd.concat([test,test_pca_2],axis=1)
### pca降维:第三组 ###
pca_3 = PCA(n_components=1)
train_col_3 = pca_3.fit_transform(train_col_3)
test_col_3 = pca_3.transform(test_col_3)
train_pca_3 = pd.DataFrame(train_col_3,columns=['pca3'])
test_pca_3 = pd.DataFrame(test_col_3,columns=['pca3'])
train.drop(col_pca_3,axis=1,inplace=True)
test.drop(col_pca_3,axis=1,inplace=True)
train = pd.concat([train,train_pca_3],axis=1)
test = pd.concat([test,test_pca_3],axis=1)
### 保存新数据 ###
train.to_csv("train.csv", index=False)
test.to_csv("test.csv", index=False)
3. 实验结果
相比第一次试验结果指标有所提升:
| 本地测试 | 训练集测试 |
|---|---|
| 0.7268395109024496 | 0.7256975890664609 |
3.第三次试验
第三次实验的目标是寻找模型最适合的参数,从而提升准确率。
1. 确定有效参数
LGBMClassifier模型中主要参数有一下几种:
- num_leaves 树的最大叶子数,对比xgboost一般为2的max_depth幂次
- max_depth 最大树的深度
- learning_rate 学习率
- n_estimators 拟合的树的棵树,相当于训练轮数
- subsample_for_bin 用来构建直方图的数据的样本数量
- min_child_samples 一个叶子节点中最小的数据量,调大可以防止过拟合
利用GridSearchCV对以上参数分别单独进行调整后发现,num_leaves在30时模型准确率最高;learning_rate在0.02时模型准确率最高;n_estimators在在2000时模型准确率最高;而max_depth, subsample_for_bin, min_child_samples各项单独变化时均不影响模型准确率,因此后续不再讨论这三项参数的变化。
2.确定最优参数组合
在上一步中已经确定了num_leaves, learning_rate, n_estimators单项变化时的最优范围,还需要使用GridSearchCV找出这三项参数的最优组合,代码如下:
parameters = {
"num_leaves" : [28,30,32]
,"learning_rate" : [0.01,0.02,0.05]
,"n_estimators" : [1500,2000,3000]
}
### 初始化模型 ###
gbm = lgb.LGBMClassifier(num_leaves=30
,max_depth=5
,learning_rate=.02
,n_estimators=1000
,subsample_for_bin=5000
,min_child_samples=200
,colsample_bytree=.2
,reg_alpha=.1
,reg_lambda=.1)
### kFold在原集合上测试 ###
kf = KFold(n_splits=10, shuffle=True, random_state=100)
### GridSearchCV设置超参数网格搜索 ###
gsearch = GridSearchCV(gbm, param_grid=parameters, scoring='accuracy', cv=3)
# 直接在训练集上找最优参数
gsearch.fit(train, target.values.ravel())
print("Best score: %0.3f" % gsearch.best_score_)
print("Best parameters set:")
best_parameters = gsearch.best_estimator_.get_params()
for param_name in sorted(parameters.keys()):
print("\t%s: %r" % (param_name, best_parameters[param_name]))
最优组合结果为:
Best score: 0.805
Best parameters set:
learning_rate: 0.02
n_estimators: 2000
num_leaves: 30
3.实验结果
将前两步中得到的最优模型参数代入后,实验结果如下,可以看出准确率有所提升。
| 本地测试 | 训练集测试 |
|---|---|
| 0.727115132504674 | 0.72640380735171839 |
资源下载地址:https://download.csdn.net/download/sheziqiong/85884404
资源下载地址:https://download.csdn.net/download/sheziqiong/85884404