构建贝叶斯网络_MATLAB学习笔记（1）

本文是利用matlab贝叶斯网络构建工具FullBNT创建一个贝叶斯网络并做一些简单的推理工作的一个学习笔记。

一、原理

贝叶斯网络的原理是贝叶斯定理。
利用贝叶斯网络解决推理问题的核心就是，利用已知的“正向概率”求解“逆向概率”。

二、构建贝叶斯网络

1、安装贝叶斯网络构建工具FullBNT

工具的安装可以参考《利用matlab进行简单的贝叶斯网络构建》。文章中提到的在命令行中输入命令 ：`

    cd D:\MATLAB7\toolbox\FullBNT-1.0.4

会报错，应改为：

    cd 'D:\MATLAB7\toolbox\FullBNT-1.0.4'

其他的都没有问题，按大佬的教程能安装成功。

2、着手构建网络

贝叶斯网络的构成包括：(1)无向环；(2)条件概率表集合。所以贝叶斯网络的创建也主要包括这两大部分，这个过程在matlab中的具体实现步骤如下，前五步是在创建一个对应的无向环，最后一步赋值条件概率：
（1）创建矩阵（无向环在matlab用矩阵构建）
（2）给各个结点编号（按拓扑逻辑结构编号）
（3）结点之间相关性赋值（有关系的赋值为1）
（4）定义结点的类型和大小（不同的节点定义为不同的类型，大小是该节点的可能性的种类，比如对于下雨，定义它有两种可能，下雨和不下雨，那么其大小为2）
（5）通过工具箱中的语句创建一个网络
（6）给每个关系赋予对应的条件概率

【例子1】

此例子来着《利用matlab进行简单的贝叶斯网络构建》。


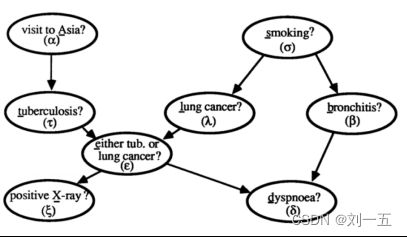
（1）创建贝叶斯网络的matlab程序：

clear all;
N=8;
dag=zeros(N,N);%创建无环图对应的矩阵
A=1;S=2;T=3;L=4;B=5;E=6;P=7;D=8;%按拓扑矩阵给各个节点编号
dag(A,T)=1;%按拓扑结构关系赋值
dag(S,L)=1;
dag(S,B)=1;
dag(T,E)=1;
dag(L,E)=1;
dag(E,P)=1;
dag(E,D)=1;
dag(B,D)=1;
discrete_nodes = 1:N;%赋予各个节点类型，用1：N表示各个节点种类不同
node_sizes = 2*ones(1,N);%赋予节点的大小,节点独立地有几种可能
bnet=mk_bnet(dag,node_sizes,'names',{'A','S','T','L','B','E','P','D'},'discrete',discrete_nodes);%创建节点
bnet.CPD{A}=tabular_CPD(bnet,A,[0.99,0.01]);%赋概率值
bnet.CPD{S}=tabular_CPD(bnet,S,[0.50,0.50]);
bnet.CPD{T}=tabular_CPD(bnet,T,[0.99,0.95,0.01,0.05]);
bnet.CPD{L}=tabular_CPD(bnet,L,[0.99 0.9 0.01 0.1]);
bnet.CPD{B}=tabular_CPD(bnet,B,[0.70,0.40,0.30,0.60]);
bnet.CPD{E}=tabular_CPD(bnet,E,[1,0,0,0,0,1,1,1]);
bnet.CPD{P}=tabular_CPD(bnet,P,[0.95,0.02,0.05,0.98]);
bnet.CPD{D}=tabular_CPD(bnet,D,[0.9,0.2,0.3,0.1,0.1,0.8,0.7,0.9]);
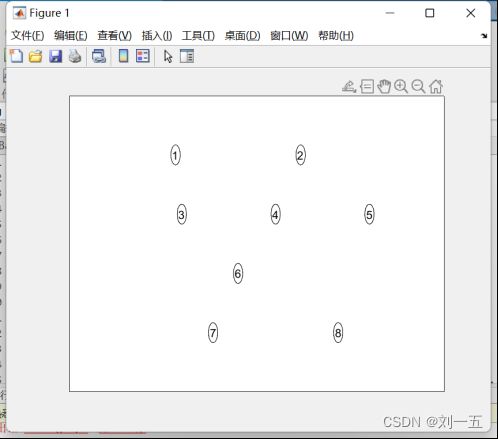
draw_graph(dag)

（2）构建完成的贝叶斯网络：

【例子2】

此例子来着《How to use the Bayes Net Toolbox》.

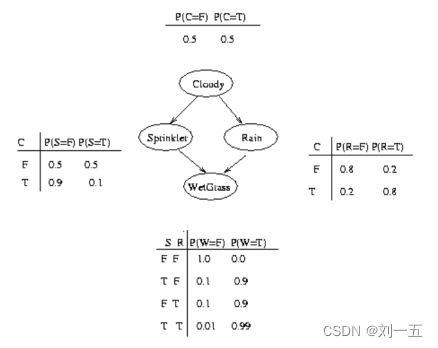
（1）创建贝叶斯网络的matlab程序：

clear all;
N=4;
dag=zeros(N,N);%无向环用矩阵表示
C=1;S=2;R=3;W=4;%按拓扑矩阵给各个节点编号,方便下一步赋值
dag(C,[R S])=1;%按逻辑关系赋值
dag([S R],W)=1;
discrete_nodes = 1:N;%定义类型
node_sizes = 2*ones(1,N);%分配大小
bnet=mk_bnet(dag,node_sizes,'names',{'C','S','R','W'},'discrete',discrete_nodes);%创建网络
bnet.CPD{C}=tabular_CPD(bnet,C,[0.5 0.5]);%赋上各个事件的概率值
bnet.CPD{S}=tabular_CPD(bnet,S,[0.5 0.9 0.5 0.1]);
bnet.CPD{R}=tabular_CPD(bnet,R,[0.8 0.2 0.2 0.8]);
bnet.CPD{W}=tabular_CPD(bnet,W,[1.0 0.1 0.1 0.01 0 0.9 0.9 0.99]);
draw_graph(dag) %绘制出贝叶斯网络图

（2）构建完成的贝叶斯网络：

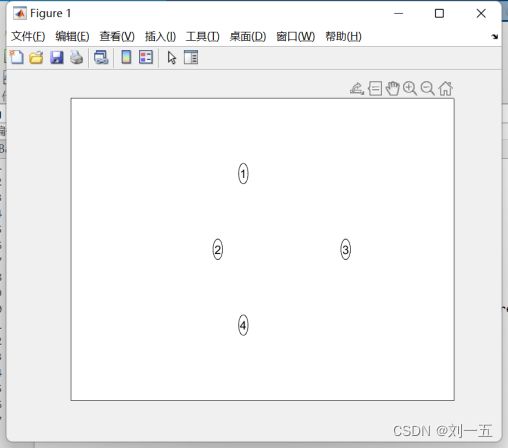
Notice1：

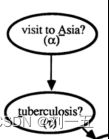
在表达这个逻辑关系时，是 dag(A,T)=1，而不是dag(T,A)=1.

Notice2：
节点的大小仅表示节点在独立情况下有多少种可能性，比如像上图中的节点A，是否去过亚洲，可能的结果有两种，去过和没去过，那么节点的大小就是2.

Notice3：
这里的概率值是有一定的先后顺序的，
（1）只有两个概率值时：F T（其实也就是 0 1）
（2）有四个概率值时，按下面这个例子，PC：FF FT TF TT（其实也就是00 01 10 11）

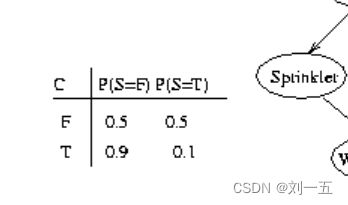
（3）有八个概率值时，按下面的这个例子，WRS：FFF FFT FTF FTT TFF TFT TTF TTT（其实也就是000 001 010 011 100 101 110 111）

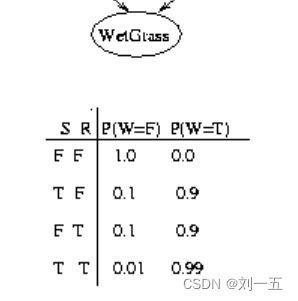
By the way，这里PC、WRS遵循的规律是：
不同级时，下面的排在前；
同一级时，右面的排在前。

三、构建贝叶斯网络后要解决什么问题

比如对于【例子2】，在建立贝叶斯网络之后，可以根据观察到的现象推测原因；下面是计算当观察到玻璃是湿的时候，下雨的可能性有多大的matlab程序片段：

engine=jtree_inf_engine(bnet); %结树，贝叶斯网络，创建一个"引擎"
evidence=cell(1,N);
evidence{W}=2;%计算当观察到玻璃是湿的时候，下雨的可能性有多大
[engine,loglik]=enter_evidence(engine,evidence);
m=marginal_nodes(engine,C);
m.T

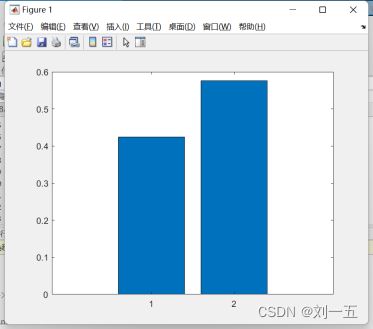
计算结果如下图所示，表明当观察到玻璃是湿的的时候，没有下雨的可能性是42.42%，下过雨的可能性是57.58%。

也可以用柱状图表示出来：

bar(m.T)

参考：
【1】https://blog.csdn.net/liubaobei199209/article/details/78810977
【2】https://www.cs.ubc.ca/~murphyk/Software/BNT/usage.html#examples
【3】https://blog.csdn.net/weixin_39716877/article/details/111158278