MeanShift- 案例实现(python)
MeanShift
- Mean Shift聚类算法
-
- 背景介绍
- 效果展示
- 模型概览
-
- 模型定义
- 训练过程
- 数据集
-
- 数据集介绍
- 训练
-
- 01 - 读入数据
- 02 - 求解meanshift向量
- 03 - 聚类
- 04 - 绘图
- 05 - 主函数
- 运行结果
- 总结
- 参考文献
Mean Shift聚类算法
Mean Shift算法是一种无参密度估计算法,Mean Shift算法在很多领域都有成功应用,例如图像平滑、图像分割、物体跟踪等,这些属于人工智能里面模式识别或计算机视觉的部分,另外也包括常规的聚类应用。
背景介绍
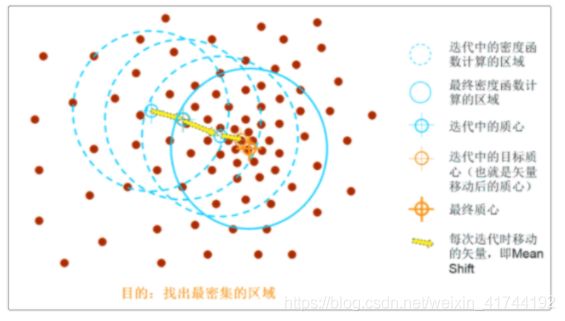
通过名字就可以看到该算法的核心,mean(均值),shift(偏移),Mean Shift算法所做的工作是找到数据概率密度最大的区域。以二维来说明可能更容易理解,下图中的很多的红点就是我们的样本特征点,meanshift会依次选中每一个点为圆心(质心),在选中一个点后,然后以半径R画一个圆,然后落在这个圆中的每一个点与圆心都会构成一个向量,把所有这些向量相加,我们会得到一个向量,就是下图中用黄色箭头表示的向量,这个向量就是meanshift向量。然后再以这个meanshift向量的终点为圆心,继续上述过程,又可以得到一个meanshift向量,然后不断地继续重复这样的过程,我们可以得到很多连续的meanshift向量,这些向量首尾相连,最终迭代到收敛,在某处停下来。最后的那个meanshift向量的终点就是最终得到的结果(最终质心),如下图:
效果展示
我们使用meanshift算法对商城消费者的数据进行聚类,下面的散点图为聚类结果,其中每个点的横坐标代表消费者的消费积分,纵坐标代表消费者的年收入,星形标记代表不同的聚类。

模型概览
模型定义
在商城统计的消费者数据中,与消费者有关的数据有4条,分别为性别,年龄,年收入,消费产生的积分。现对消费者进行聚类,我们选取年收入与消费积分数据作为样本特征点,在2维空间n个样本点中 x i , i = 1 , ⋯ , n x_{i}, i=1, \cdots, n xi,i=1,⋯,n,对于其中的一个样本的候选质心 x x x,其中 N ( x ) N\left(x\right) N(x)是围绕 x x x 周围一个给定距离范围内的样本邻域, 通过计算其他所有样本点 y y y与 x x x的距离,小于区域半径 r r r的点即表示落在区域内, N ( x i ) N\left(x_{i}\right) N(xi)定义为下:
N h ( x ) = ( y ∣ ( y − x ) ( y − x ) T ⩽ r 2 ) N_{h}(x)=\left(y \mid(y-x)(y-x)^{T} \leqslant r^{2}\right) Nh(x)=(y∣(y−x)(y−x)T⩽r2)
再通过更新质心的候选位置,到达最终质心,这些侯选位置通常是所选定区域内点的均值,则对于 x x x点,其Mean Shift向量的基本形式为:
M h ( x ) = 1 k ∑ x i ∈ N h ( x i − x ) M_{h}(x)=\frac{1}{k} \sum_{x_{i} \in N_{h}}\left(x_{i}-x\right) Mh(x)=k1xi∈Nh∑(xi−x)
∥ m h ( x ) − x ∥ < ε \left\|m_{h}(x)-x\right\|<\varepsilon ∥mh(x)−x∥<ε
M h M_{h} Mh 是均值偏移向量(mean shift vector), 该向量是所有质心中指向点密度增加最多的区域的偏移向量, k k k表示区域内的样本点数量。在不断迭代的过程中,质心不断更新,当更新后的质心与原质心变化小于一定阈值 ε \varepsilon ε时(此值在以下实现算法中定义为区域半径),发生收敛,结束循环。对其他样本点重复以上步骤,可求得每个样本的最终质心。有了质心即可根据样本点密度来进行分类了。
训练过程
通过以下几个步骤进行模型训练
- 在未被标记的数据点中依次选择作为起始中心点C。
- 以C为质心作半径为radius的圆,得到区域中出现的所有数据点,则设这些点同属于一个聚类A。同时在该聚类中记录数据点出现的频率次数加1。
- 以C为中心点,得到从C开始到区域内每个样本的向量,将这些向量相加,得到向量Shift。C沿着Shift的方向移动到Shift的终点。
- 重复步骤2、3,直到shift向量不在发生变化(迭代到收敛),记住此时的C。且这个迭代过程中遇到的点都归类到A。
- 如果收敛时当前类A的质心与其它已经存在的类A2质心的距离小于半径(也可设为其他阈值),那么把A2和A合并,数据点出现次数也对应合并。否则,把A作为新的类,并保存。
- 重复1、2、3、4、5直到所有的点都被标记为已访问。
- 分类:根据每个类对每个点的访问频率,取访问频率最大的那个类,作为当前点集的所属类。
数据集
数据集介绍
此数据集共200行,每行包含了消费者的相关信息与消费数据。其各维属性的意义如下:
| 属性名 | 解释 | 类型 |
|---|---|---|
| Customer | 消费者编号 | 连续值 |
| Gender | 消费者性别 | 离散值 |
| Age | 消费者年龄 | 离散值 |
| Annual Income (k$) | 消费者的年收入 | 离散值 |
| Spending Score (1-100) | 消费产生的积分 | 离散值 |
训练
首先我们引入必要的库:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from tqdm.notebook import tqdm
01 - 读入数据
param:
- file_path:数据存储路径
return:
- data:样本特征数据
def load_data(file_path):
customers_data = pd.read_csv("meanshift_data/Mall_Customers.csv")# 读入样本数据
data = customers_data.iloc[:, [3, 4]].values # 获取收入与消费积分数据
return data
02 - 求解meanshift向量
param:
- data:样本特征数据
- radius:样本区域半径
return:
- clusters:所有样本点聚类结果
def mean_shift(data, radius=2.5):
clusters = []#存储每个样本所属的质心与出现频次
for i in tqdm(range(len(data))):
# 每个数据点都做为初始聚类的质心
cluster_centroid = data[i] # 初始质心
cluster_frequence = np.zeros(len(data)) # 初始每个数据点的聚类频率
# 遍历数据点
while True:
temp_data = []#存储半径内的所有数据集
for j in range(len(data)): # 每次都遍历所有元素
v = data[j] # 获取第j个点
if np.linalg.norm(v - cluster_centroid)<= radius:#判断样本是否在圆区域内
temp_data.append(v)# 把半径内的所有数据集合起来
cluster_frequence[i] += 1 # 在当前聚类中记录数据点出现的次数加1
old_centroid = cluster_centroid # 旧的质心
new_centroid = np.average(temp_data,axis=0)# 新的质心
cluster_centroid = new_centroid # 更新质心
# 如果新旧质心一致,出现收敛,则结束
if np.array_equal(new_centroid,old_centroid):
# 判断是否出现重复聚类
has_same_cluster = False
for cluster in clusters:
# 两个质心小于半径,则为同一个聚类
if np.linalg.norm(cluster['centroid'] - cluster_centroid)<= radius:
has_same_cluster = True
#合并,数据点出现次数也对应合并。
cluster['frequency'] = cluster['frequency'] + cluster_frequence
#出现重复的类,跳出,直接进行下一个样本点计算
if has_same_cluster:
break
#如果质心不同,保存质心,记录数据频次,并跳出,进行下一个样本点计算
if not has_same_cluster:
clusters.append({
'centroid':cluster_centroid,
'frequency':cluster_frequence
})
break
return clusters
03 - 聚类
根据样本点在所有聚类中出现的频率,取对其访问频率最大的那个类,作为当前点的所属类。
param:
- data:样本特征数据
- clusters:所有聚类结果
return:
- index:最终聚类数量
def clustering(data, clusters):
t = []
index=[]
for cluster in clusters:
cluster['data'] = []
t.append(cluster['frequency'])
t = np.array(t)
# 聚类
for i in range(len(data)):
column_frequency = t[:, i]
cluster_index = np.where(column_frequency == np.max(column_frequency))[0][0]#得到频率最大的类索引
index.append(cluster_index)#记录索引
clusters[cluster_index]['data'].append(data[i])#将样本点添加到所属类
return np.unique(index)
04 - 绘图
param:
- clusters:所有聚类结果
- index:最终聚类数量
def draw(index,clusters):
fig = plt.figure(figsize=(20,7))
axes = fig.add_subplot(111)
colour=['magenta','cyan','pink','red','orange','green','blue']#创建一个颜色库
# 画出每个类质心
for i in index:
axes.scatter(clusters[i]['centroid'][0], clusters[i]['centroid'][1], marker='*', s=260, linewidths=3, color='black', label='centroid')
# 画出样本聚类结果
for i in tqdm(index):
for j in range(len(clusters[i]['data'])):
axes.scatter(clusters[i]['data'][j][0], clusters[i]['data'][j][1], color=colour[i],alpha=1)
x_min, x_max = min(data[:,0])-10, max(data[:,0])+10 # 横轴坐标范围
y_min, y_max = min(data[:,1])-1, max(data[:,1])+1 # 纵轴坐标范围
plt.title("Mean Shift clustering") # 标题
plt.show()
05 - 主函数
if __name__ == "__main__":
data = load_data("meanshift_data/Mall_Customers.csv")
print("1、导入数据:",len(data),"条")
print("2、求解MeanShift向量")
clusters=mean_shift(data, radius=18)
index = clustering(data, clusters)
print("3、聚类数量为:",len(index))
print("4、绘图")
draw(index,clusters)
运行结果
总结
介绍了meanshift聚类算法的基本概念,算法原理以及具体实现过程。并借助消费者数据集,建立模型,实现了根据消费者的特征进行分类的模型训练过程。
参考文献
- http://www.scikitlearn.com.cn/0.21.3/22/#234-mean-shift
- Mean shift: A robust approach toward feature space analysis.” D. Comaniciu and P. Meer, IEEE Transactions on Pattern Analysis and Machine Intelligence (2002)
