Quaternion kinematics for error state kalman filter实现GPS+IMU融合，（附源码）

最近在学习kalman滤波相关的知识，恰好工作可能需要使用ESKF算法，因此将Joan Sola大神的书看了一遍，同时推导了相关的公式。俗话说得好：“Talk is cheap, show me the code。"因此我就想着如何将文章里面的算法实现一遍，加深对算法的记忆。

在网上查阅资料时，看到了博主利用高精度IMU模型实现了GPS+IMU的ESKF融合，这不巧了，数据啥的就都有了，只需要将代码的核心部分修改一下就可以了。

首先就是将源代码看了一遍，搞懂了输入输出，于是对代码进行了改写。附上github地址:GitHub - Shelfcol/gps_imu_fusion at Qk-ESKF-dev

（引流我的EKF实现GPS+IMU的融合）

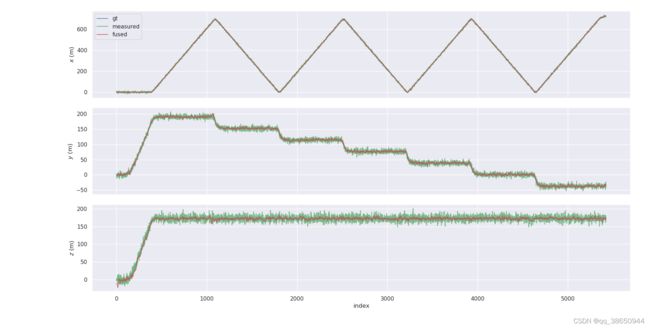
先上效果图：（感觉还不错，gnss-ins-sim使用得low-accuracy IMU）

 下面对算法进行讲解，并给出相应得代码段。

本文使用的名义状态量， 误差状态量为,这里需要注意一下，名义状态量多一维是因为利用四元数表示的旋转。

名义状态运动学方程为： 

使用上述公式在IMU数据到来的预测阶段进行状态的预测：（需要注意的是，这里使用的IMU的加速度和角速度都是使用的IMU局部坐标系下的数值）

bool ESKFQK::UpdateOdomEstimation(const Eigen::Vector3d& a_m, const Eigen::Vector3d& w_m, const double dt) {
    // 计算位置
    Eigen::Matrix3d R = q_.toRotationMatrix();
    
    pose_ += velocity_*dt+0.5*(R*(a_m-accel_bias_)+g_)*dt*dt;
    velocity_ += (R*(a_m-accel_bias_)+g_)*dt;

    Eigen::Vector3d d_theta = (w_m-gyro_bias_)*dt;
    Eigen::AngleAxisd dq(d_theta.norm(),d_theta.normalized());//!
    q_ = q_*Eigen::Quaterniond(dq);

    return true;
}

（矩阵块太难打，所以直接截图）

误差状态动力学公式为：

 这里需要注意的就是的更新：书上使用的是生成的旋转矩阵的转置来旋转原本的。而我根据s上的公式(155)

所以对 的更新使用的公式为 

 

公式157c的推导没搞明白，如果有理解的仁兄还望不吝赐教。

完全是利用误差状态动力学公式推导而来，这里不再赘述，直接贴图。需要注意的是误差状态的预测方程(164)是无用的，因为在只有IMU数据时，误差状态为0，所以(164)没有实质作用。

 对应的代码块：

bool ESKFQK::UpdateErrorState(const Eigen::Vector3d& a_m, const Eigen::Vector3d& w_m, const double dt) {
    Eigen::Matrix3d A_M = BuildSkewMatrix(a_m-accel_bias_);

    // Fx
    Fx_.setZero(); // 初始化为零矩阵
    Fx_.block<3,3>(0,0) = Fx_.block<3,3>(3,3) = Fx_.block<3,3>(9,9) = Fx_.block<3,3>(12,12) = Fx_.block<3,3>(15,15)= Eigen::Matrix3d::Identity();
  
    Eigen::Matrix3d R = q_.toRotationMatrix();
    Fx_.block<3,3>(INDEX_STATE_POSI,INDEX_STATE_VEL) =  Eigen::Matrix3d::Identity()*dt;
    Fx_.block<3,3>(INDEX_STATE_VEL,INDEX_STATE_ORI) =  -R*A_M*dt;
    Fx_.block<3,3>(INDEX_STATE_VEL,INDEX_STATE_ACC_BIAS) =  -R*dt;
    Fx_.block<3,3>(INDEX_STATE_VEL,INDEX_STATE_GYRO_BIAS) = Eigen::Matrix3d::Identity()*dt;
    

    Eigen::AngleAxisd  AngleAxis_w(((w_m-gyro_bias_)*dt).norm(),((w_m-gyro_bias_)*dt).normalized());
    Eigen::Matrix3d R_w(AngleAxis_w);
    Fx_.block<3,3>(INDEX_STATE_ORI,INDEX_STATE_ORI) = R_w.transpose();//公式157c
    // Fx_.block<3,3>(INDEX_STATE_ORI,INDEX_STATE_ORI) = Eigen::Matrix3d::Identity()-BuildSkewMatrix(w_m-gyro_bias_)*dt;//自己使用的公式
    
    Fx_.block<3,3>(INDEX_STATE_ORI,INDEX_STATE_GYRO_BIAS) =  -Eigen::Matrix3d::Identity()*dt;

    P_ = Fx_*P_*Fx_.transpose()+Fi_*Qi_*Fi_.transpose();
    return true;
}

当有GPS数据到来的时候，则进行观测更新。因为GPS只有位置，所以可观测的数据只有位置。则对应的

 其中的H矩阵不是关于名义状态量，而是关于误差状态量的，同时是在真实状态处获得。因为当前还没有进行观测，所以误差状态的均值为0，所以。

其中 ，这也是标准的EKF步骤中使用的观测矩阵。

而求解如下

 对应的代码如下：

bool ESKFQK::ObservationOfErrorState()
{
    Hx_.setZero();
    Hx_.block<3,3>(0,0) = Eigen::Matrix3d::Identity();
    // X_dx_;
    X_dx_.block<6,6>(0,0) = Eigen::Matrix::Identity();
    X_dx_.block<9,9>(10,9) = Eigen::Matrix::Identity();
    double qx = q_.x();
    double qy = q_.y();
    double qz = q_.z();
    double qw = q_.w();
    X_dx_.block<4,3>(6,6) = 0.5*(Eigen::Matrix()<<-qx,-qy,-qz,
                                                                qw,-qz,qy,
                                                                qz,qw,-qx,
                                                                -qy,qx,qw).finished();
    H_ = Hx_*X_dx_;

    K_ = P_ * H_.transpose() * (H_ * P_ * H_.transpose() +V_).inverse(); // kalman增益
    X_ = K_*(curr_gps_data_.position_ned - pose_);

    P_ = (TypeMatrixP::Identity() - K_ * H_) * P_*(TypeMatrixP::Identity() - K_ * H_).transpose()+K_*V_*K_.transpose();
    
}

下一步就需要将误差量加入到名义状态里面：（需要注意的是这里使用的是右乘，因为是绕动轴旋转）

// 估计值=估计值+误差量
void ESKFQK::EliminateError() {
    pose_ +=X_.block<3,1>(INDEX_STATE_POSI,0);
    velocity_ += X_.block<3,1>(INDEX_STATE_VEL, 0);
    Eigen::Matrix3d C_nn = Sophus::SO3d::exp(X_.block<3,1>(INDEX_STATE_ORI, 0)).matrix();
    q_ = q_*Eigen::Quaterniond(C_nn); 
    accel_bias_ += X_.block<3,1>(INDEX_STATE_ACC_BIAS, 0);
    gyro_bias_ += X_.block<3,1>(INDEX_STATE_GYRO_BIAS, 0);
    g_ += X_.block<3,1>(INDEX_STATE_G,0);
}

最后还需要重置ESKF：

void ESKFQK::ResetState() {
    X_.setZero();
    // P = G'PG'^T
    Eigen::Matrix  G;
    G.setIdentity();
    G.block<3,3>(6,6) -= BuildSkewMatrix(0.5*X_.block<3,1>(INDEX_STATE_ORI, 0)); 
    P_ = G*P_*G.transpose();
}

这样就大功告成啦！

说一点调参的经验，需要注意状态量的方差设置要与实际的传感器的精度对应。

参考文献：[1]J Solà. Quaternion kinematics for the error-state Kalman filter[J].  2017.

                  [2]【附源码+代码注释】误差状态卡尔曼滤波(error-state Kalman Filter)，扩展卡尔曼滤波，实现GPS+IMU融合，EKF ESKF GPS+IMU_一点儿也不萌的萌萌的博客-CSDN博客_误差卡尔曼