几个常用机器学习算法 - 最大熵模型

作者：xg123321123

出处：http://blog.csdn.net/xg123321123/article/details/54286514

声明：版权所有，转载请联系作者并注明出处

熵是随机变量不确定性的度量，不确定性越大，熵值越大；若随机变量退化成定值，熵为0。
如果没有外界干扰，随机变量总是趋向于无序，在经过足够时间的稳定演化，它应该能够达到的最大程度的熵。
假设离散随机变量 X 的概率分布是P(X)，则其熵是

H(P)=−∑xP(x)logP(x)

且熵满足下列不等式：

0≤H(P)≤log|X|

其中 |X| 是 X 的取值个数，当且仅当X 的分布是均匀分布时右边的等号成立，这就是说，当 X 服从均匀分布时，熵最大。

1 最大熵原理

为了准确的估计随机变量的状态，我们一般习惯性最大化熵，认为在所有可能的概率模型（分布）的集合中，熵最大的模型是最好的模型。
换言之，在已知部分知识的前提下，关于未知分布最合理的推断就是符合已知知识最不确定或最随机的推断，其原则是承认已知事物（知识），且对未知事物不做任何假设，没有任何偏见。

例如，投掷一个骰子，如果问”每个面朝上的概率分别是多少”，你会说是等概率，即各点出现的概率均为1/6。因为对这个”一无所知”的色子，什么都不确定，而假定它每一个朝上概率均等则是最合理的做法。
从投资的角度来看，这是风险最小的做法，而从信息论的角度讲，就是保留了最大的不确定性，也就是说让熵达到最大。

所以，最大熵原理也可以表述为在满足约束条件的模型集合中选取熵最大的模型。

2 无偏原则

下面抄来一个有关最大熵模型的文章中都喜欢举的例子。

例如，一篇文章中出现了“学习”这个词，那这个词是主语、谓语、还是宾语呢？换言之，已知“学习”可能是动词，也可能是名词，故“学习”可以被标为主语、谓语、宾语、定语等等。

令x1表示“学习”被标为名词， x2表示“学习”被标为动词。
令y1表示“学习”被标为主语， y2表示被标为谓语， y3表示宾语， y4表示定语。

且这些概率值加起来的和必为1，即:

p(x1)+p(x2)=1

p(y1)+p(y2)+p(y3)+p(y4)=1

则根据无偏原则，认为这个分布中取各个值的概率是相等的，故得到：

p(x1)=p(x2)=0.5

p(y1)=p(y2)=p(y3)=p(y4)=0.25

因为没有任何的先验知识，所以这种判断是合理的。如果有了一定的先验知识呢？
即进一步，若已知：“学习”被标为定语的可能性很小，只有0.05，即

p(y4)=0.05

剩下的依然根据无偏原则，可得：

p(x1)=p(x2)=0.5

p(y1)=p(y2)=p(y3)=0.953

再进一步，当“学习”被标作名词x1的时候，它被标作谓语y2的概率为0.95，即

p(y2|x1)=0.95

此时仍然需要坚持无偏见原则，使得概率分布尽量平均。但怎么样才能得到尽量无偏见的分布？

熵的理论中，在完全无约束状态下，均匀分布等价于熵最大（有约束的情况下，不一定是概率相等的均匀分布。 比如，给定均值和方差，熵最大的分布就变成了正态分布 ）。
于是，问题便转化为了：计算X和Y的分布，使得H(Y|X)达到最大值，并且满足下述条件：

p(x1)+p(x2)=1

p(y1)+p(y2)+p(y3)+p(y4)=1

p(y4)=0.05

p(y2|x1)=0.95

因此，也就引出了最大熵模型的本质，它要解决的问题就是已知X，计算Y的概率，且尽可能让Y的概率最大（实践中，X可能是某单词的上下文信息，Y是该单词翻译成me，I，us、we的各自概率），从而根据已有信息，尽可能最准确的推测未知信息，这就是最大熵模型所要解决的问题。

相当于已知X，计算Y的最大可能的概率，转换成公式，便是要最大化下述式子H(Y|X)：

maxH(Y|X)=∑{x∈x1,x2}{y∈y1,y2,y3,y4}p(x,y)log1p(y|x)

且满足以下4个约束条件：

p(x1)+p(x2)=1

p(y1)+p(y2)+p(y3)+p(y4)=1

p(y4)=0.05

p(y2|x1)=0.95

3.2 最大熵模型的表示

有了目标函数跟约束条件，我们就能写出最大熵模型的一般表达式了：

maxH(Y|X)p∈P=∑(x,y)p(x,y)log1p(y|x)

其中，P={p | p是X上满足条件的概率分布}
继续阐述之前，先定义特征、样本和特征函数。
特征：(x,y)

• y：这个特征中需要确定的信息
• x：这个特征中的上下文信息

样本：关于某个特征(x,y)的样本，特征所描述的语法现象在标准集合里的分布： (xi,yi) 对，其中， yi 是y的一个实例， xi 是 yi 的上下文。
对于一个特征 (x0,y0) ，定义特征函数：

f(x,y)=(1:如果y=y0且x=x00:其他情况)

特征函数关于经验分布 p¯(x,y) 在样本中的期望值是：

p¯(f)=∑(xi,yi)p¯(x,y)f(x,y)

其中 p¯(x)=x出现的概率 ， p¯(x,y)=x和y同时出现的概率

特征函数关于模型P(Y|X)与经验分布 P¯(X) 的期望值为：

p(f)=∑(xi,yi)p(xi,yi)f(xi,yi)

=∑(xi,yi)p(yi|xi)p(xi)f(xi,yi)

=∑(xi,yi)p(yi|xi)p¯(xi)f(xi,yi)

如果能够获取训练数据中的信息，那么上述这两个期望值相等，即：

p(f)=p¯(f)

将上式作为模型学习的约束条件，假如有n个特征函数 fi(x,y) ,那么就有n个约束条件。

从而得到最大熵模型的完整表述如下：

p^=arg⋅maxp∈P∑(x,y)p(y|x)p¯(x)log1p(y|x)

其约束条件为：

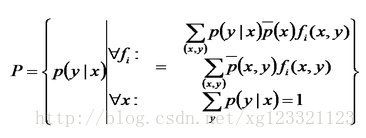
也就是说，让定义在条件概率分布 P(Y|X) 上的条件熵 H(P) 最大的模型称作最大熵模型，其中

H(P)=−∑(x,y)p(y|x)p¯(x)log⋅p(y|x)

3.3 最大熵模型的学习

上述问题已知若干条件，要求若干变量的值使到目标函数（熵）最大，其数学本质是最优化问题（Optimization Problem），其约束条件是线性的等式，而目标函数是非线性的，所以该问题属于非线性规划（线性约束）(non-linear programming with linear constraints)问题，故可通过引入拉格朗日函数将原有约束的最优化问题转换为无约束的最优化的对偶问题。

最大熵模型的学习等价于约束最优化问题：

maxp∈CH(P)=−∑(x,y)p¯(x)p(y|x)log⋅p(y|x)

其中，约束条件为:

p(fi)=p¯(fi),i=1,2,...,n

∑yp(y|x)=1

按照最优化问题的习惯，将求最大值问题改写为等价的求最小值问题：

minp∈C(−H(P))=∑(x,y)p¯(x)p(y|x)log⋅p(y|x)

其中，约束条件为:

p(fi)−p¯(fi)=0,i=1,2,...,n

∑yp(y|x)=1

求解上面式子，得出的解，就是最大熵模型学习的解。

这里，将约束最优化的原始问题转换为无约束最优化的对偶问题，通过求解对偶问题求解原始问题。

先引进拉格朗日乘子 w0,w1,...,wn ,定义拉格朗日函数 L(P,w) :

L(P,w)=−H(P)+w0⎛⎝1−∑yp(y|x)⎞⎠+∑i=1nwi(p¯(fi)−p(fi))

=∑x,yp¯(x)p(y|x)log⋅p(y|x)+w0⎛⎝1−∑yp(y|x)⎞⎠+∑i=1nwi⎛⎝∑x,yp¯(x,y)fi(x,y)−∑x,yp¯(x)p(y|x)fi(x,y)⎞⎠

最优化的原始问题是

minp∈CmaxwL(P,w)

对偶问题是

maxwminp∈CL(P,w)

由于拉格朗日函数 L(P,w) 是P的凸函数，原始问题的解与对偶问题的解是等价的

这样一来，就可以通过求解对偶问题来求解原始问题：

首先，求解对偶问题内部的极小化问题 minp∈CL(P,w)
minp∈CL(P,w) 是 w 的函数，记为

ψ(w)=minp∈CL(P,w)=L(Pw,w)

ψ(w) 就称为对偶函数，同时，将其解记为

Pw=arg⋅minP∈CL(P,w)=pw(y|x)....(why?)

具体的，求 L(P,w) 对 P(y|x) 的偏导数

∂L(P,w)∂P(y|x)=∑x,yp¯(x)(log⋅p(y|x)+1)−∑yw0−∑x,y(p¯(x)∑i=1nwifi(x,y))

=∑x,yp¯(x)(log⋅p(y|x)+1−w0−∑i=1nwifi(x,y))

令偏导数等于0，在 p¯(x)>0 的条件下，解得

p(y|x)=exp(∑i=1nwifi(x,y)+w0−1)

=exp(∑ni=1wifi(x,y))exp(1−w0)

由于 ∑yP(y|x)=1 ,得

Pw(y|x)=exp(∑ni=1wifi(x,y))Zw(x)

其中

Zw(x)=∑yexp(∑i=1nwifi(x,y))

Zw(x) 就称为规划化因子；而 fi(x,y) 是特征函数； wi 是特征的权值

而 Pw=Pw(y|x) 就是最大熵模型，这里 w 是最大熵模型的参数向量

然后求解对偶问题外部的极大化问题

maxwψ(w)

将其解记为 w∗ ,即

w∗=arg⋅maxwψ(w)

在这里，可以用最优化算法求对偶函数 ψ(w) 的极大化，得到 w∗ ，用来表示 P∗∈C

而 P∗=Pw∗=Pw∗(y|x) 就是学习到的最优模型（最大熵模型），亦即，最大熵模型的学习归结为对偶函数 ψ(w) 的极大化