深入浅出理解机器学习算法—神经网络(前向传播)
一、神经网络表述
我们之前学的,无论是线性回归还是逻辑回归都有这样一个缺点,即:当特征太多时,计算的负荷会非常大。
那特征能有多大呢?下面是一个计算机视觉中的例子:

如上图所示,如果选取一小块 50 ∗ 50 50*50 50∗50像素的灰度图片(一个像素只有亮度一个值),选择每个像素点作为特征,则特征总量 n = 2500 n=2500 n=2500,换算成RGB,一个像素有三个值,则 n = 7500 n=7500 n=7500,如果将其两两组合成新特征,则特征数量为 C 2500 2 = 2500 ! 2 ≈ 3 m i l l o n C_{2500}^2=\frac{2500!}{2}\approx 3\;millon C25002=22500!≈3millon。
普通的逻辑回归模型,不能有效的处理这么多的特征,所以需要神经网络算法。
二、模型表示1
先看一下大脑的神经元长什么样:
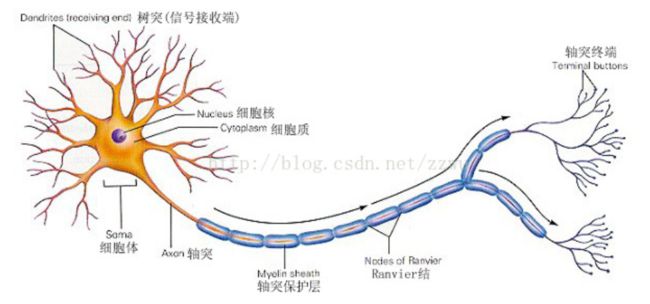
想象一下印刷厂中流水线的工人,每个工人都有特定的任务,比如装订,塑封,贴防伪标识等等,工人们看到书本并处理完自己的任务后,就回放回传送带,紧接着传送带就传给下一个环节的工人,如此不断重复从而完成一个又一个环节,直到一本书印制完成。
那么类比一下,把上图中的细胞核类比成工人,轴突类比传送带,树突则比类比成工人的双眼。一个又一个细胞体,从树突接收需要处理的信息,对其进行处理后,再经由轴突通过电信号把处理完的信息传递出去,直到理解信息的内容。
人工神经网络中,树突对应输入(input),细胞核对应激活单元(activation unit),轴突对应输出(output)。
我们一般把神经网络划分为三部分(注意,不是只有三层!),即输入层(input layer),隐藏层(hidden layer)和输出层(output layer)。
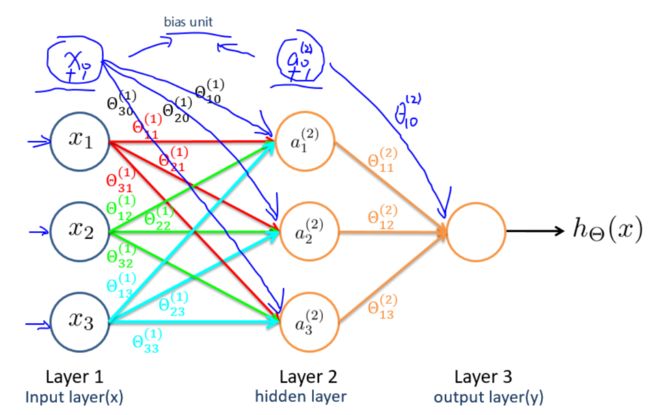
具体如下图所示:
图中的一个圈表示神经网络中的一个激活单元,输入层对应输入单元,隐藏层对应中间单元,输出层则对应输出单元。
中间激活单元应用激活函数(activation_function)处理数据。
下面列出一些已有概念在神经网络中的别称:
- x 0 x_0 x0:偏置单元, x 0 = 1 x_0=1 x0=1;
- Θ \Theta Θ:权重,即参数;
- 激活函数: g g g,即逻辑函数等;
- 输入层: 对应于训练集中的特征 x x x;
- 输出层: 对应于训练集中的结果 y y y;
- a i ( j ) a_i^{(j)} ai(j):第 j j j层第 i i i个激活单元;
- Θ ( j ) \Theta^{(j)} Θ(j):从第 j j j层映射到第 j + 1 j+1 j+1层时的权重矩阵;
- Θ v , μ ( j ) \Theta_{v,\mu}^{(j)} Θv,μ(j):从第 j j j层的第 μ \mu μ个单元映射到第 j + 1 j+1 j+1层的第 v v v个单元的权重;
- s j s_j sj:第 j j j层的激活单元数目(不包含偏置单元)。
每个单元会作用于下一层的所有单元(矩阵乘法运算)。
如果第 j j j层有 s j s_j sj个单元,第 j + 1 j+1 j+1层有 s j + 1 s_{j+1} sj+1个单元, 则 Θ j \Theta_j Θj是一个 s j + 1 ∗ ( s j + 1 ) s_{j+1}*(s_j+1) sj+1∗(sj+1)维的权重矩阵。即每一层的权重矩阵大小都是非固定的。
其中, + 1 +1 +1来自于偏置单元,这样意味着输出层不包含偏置单元,输入层和隐藏层需要添加偏置单元。
依据本节所给模型,有:
s i z e ( Θ ( 1 ) ) = s j + 1 ∗ ( s j + 1 ) = s 2 ∗ ( s 1 + 1 ) = 3 × 4 size(\Theta^{(1)})=s_{j+1}*(s_j+1)=s_2*(s_1+1)=3\times 4 size(Θ(1))=sj+1∗(sj+1)=s2∗(s1+1)=3×4
s i z e ( Θ ( 2 ) = s j + 1 ∗ ( s j + 1 ) = s 3 ∗ ( s 2 + 1 ) = 1 × 4 size(\Theta^{(2)}=s_{j+1}*(s_j+1)=s_3*(s_2+1)=1\times 4 size(Θ(2)=sj+1∗(sj+1)=s3∗(s2+1)=1×4
三、模型表示2
对输入层的所有激活单元应用激活函数,从而得到隐藏层中激活单元的值:
a 1 ( 2 ) = g ( Θ 10 ( 1 ) x 0 + Θ 11 ( 1 ) x 1 + Θ 12 ( 1 ) x 2 + Θ 13 ( 1 ) x 3 ) a_1^{(2)}=g(\Theta_{10}^{(1)}x_0+\Theta_{11}^{(1)}x_1+\Theta_{12}^{(1)}x_2+\Theta_{13}^{(1)}x_3) a1(2)=g(Θ10(1)x0+Θ11(1)x1+Θ12(1)x2+Θ13(1)x3)
a 2 ( 2 ) = g ( Θ 20 ( 1 ) x 0 + Θ 21 ( 1 ) x 1 + Θ 22 ( 1 ) x 2 + Θ 23 ( 1 ) x 3 ) a_2^{(2)}=g(\Theta_{20}^{(1)}x_0+\Theta_{21}^{(1)}x_1+\Theta_{22}^{(1)}x_2+\Theta_{23}^{(1)}x_3) a2(2)=g(Θ20(1)x0+Θ21(1)x1+Θ22(1)x2+Θ23(1)x3)
a 3 ( 2 ) = g ( Θ 30 ( 1 ) x 0 + Θ 31 ( 1 ) x 1 + Θ 32 ( 1 ) x 2 + Θ 33 ( 1 ) x 3 ) a_3^{(2)}=g(\Theta_{30}^{(1)}x_0+\Theta_{31}^{(1)}x_1+\Theta_{32}^{(1)}x_2+\Theta_{33}^{(1)}x_3) a3(2)=g(Θ30(1)x0+Θ31(1)x1+Θ32(1)x2+Θ33(1)x3)
对 Layer 2中的所有激活单元应用激活函数,从而得到输出:
h Θ ( x ) = g ( Θ 10 ( 2 ) a 0 ( 2 ) + Θ 11 ( 2 ) a 1 ( 2 ) + Θ 12 ( 2 ) a 2 ( 2 ) + Θ 13 ( 2 ) a 3 ( 2 ) ) h_{\Theta}(x)=g(\Theta_{10}^{(2)}a_0^{(2)}+\Theta_{11}^{(2)}a_1^{(2)}+\Theta_{12}^{(2)}a_2^{(2)}+\Theta_{13}^{(2)}a_3^{(2)}) hΘ(x)=g(Θ10(2)a0(2)+Θ11(2)a1(2)+Θ12(2)a2(2)+Θ13(2)a3(2))
上面的计算过程被称为前向传播(Forward propagation),即从输入层开始,一层一层地向下计算并传递结果。
再回顾一下逻辑回归:
h θ ( x ) = g ( θ 0 + θ 1 x 1 + θ 2 x 2 + θ 3 x 3 ) h_{\theta}(x)=g(\theta_0+\theta_1x_1+\theta_2x_2+\theta_3x_3) hθ(x)=g(θ0+θ1x1+θ2x2+θ3x3)
是不是除了符号表示,其他都完全一样?
其实神经网络就好似回归模型,只不过输入变成了中间单元 a 1 ( j ) , a 2 ( j ) , ⋯ , a n ( j ) a_1^{(j)}\;,\;a_2^{(j)}\;,\;\cdots\;,\;a_n^{(j)} a1(j),a2(j),⋯,an(j)。从输入 x x x开始,下一层的每个激活单元都包含了上一层的所有信息(单元值),通过最优化算法不断迭代计算,激活单元能得出关于输入 x x x的更多信息,这就好像是在给假设函数加多项式。隐藏层的这些单元好似升级版的初始特征,从而能给出更好的预测。
向量化实现
a ( 1 ) = x = { x 0 x 1 x 2 x 3 } a^{(1)}=x=\left\{ \begin{matrix*} x_0 \\ x_1 \\ x_2 \\ x_3 \end{matrix*} \right\} a(1)=x=⎩ ⎨ ⎧x0x1x2x3⎭ ⎬ ⎫
Θ ( 1 ) = { Θ 10 ( 1 ) Θ 11 ( 1 ) Θ 12 ( 1 ) Θ 13 ( 1 ) Θ 20 ( 1 ) Θ 21 ( 1 ) Θ 22 ( 1 ) Θ 23 ( 1 ) Θ 30 ( 1 ) Θ 31 ( 1 ) Θ 32 ( 1 ) Θ 33 ( 1 ) } \Theta^{(1)}=\left\{ \begin{matrix} \Theta_{10}^{(1)} & \Theta_{11}^{(1)} & \Theta_{12}^{(1)} & \Theta_{13}^{(1)} \\ \Theta_{20}^{(1)} & \Theta_{21}^{(1)} & \Theta_{22}^{(1)} & \Theta_{23}^{(1)} \\ \Theta_{30}^{(1)} & \Theta_{31}^{(1)} & \Theta_{32}^{(1)} & \Theta_{33}^{(1)} \end{matrix} \right\} Θ(1)=⎩ ⎨ ⎧Θ10(1)Θ20(1)Θ30(1)Θ11(1)Θ21(1)Θ31(1)Θ12(1)Θ22(1)Θ32(1)Θ13(1)Θ23(1)Θ33(1)⎭ ⎬ ⎫
a 1 ( 2 ) = g ( z 1 ( 2 ) ) , a 2 ( 2 ) = g ( z 2 ( 2 ) ) , a 3 ( 2 ) = g ( z 3 ( 2 ) ) a_1^{(2)}=g(z_1^{(2)})\;,\;a_2^{(2)}=g(z_2^{(2)})\;,\;a_3^{(2) }=g(z_3^{(2)}) a1(2)=g(z1(2)),a2(2)=g(z2(2)),a3(2)=g(z3(2))
z ( 2 ) = { z 1 ( 2 ) z 2 ( 2 ) z 3 ( 2 ) } z^{(2)}=\left\{ \begin{matrix} z_1^{(2)}\\ z_2^{(2)}\\ z_3^{(2)} \end{matrix} \right\} z(2)=⎩ ⎨ ⎧z1(2)z2(2)z3(2)⎭ ⎬ ⎫
则有 a ( 2 ) = g ( Θ ( 1 ) a ( 1 ) ) = g ( z ( 2 ) ) a^{(2)}=g(\Theta^{(1)}a^{(1)})=g(z^{(2)}) a(2)=g(Θ(1)a(1))=g(z(2));
预测结果为:
h Θ ( x ) = a ( 3 ) = g ( Θ ( 2 ) a ( 2 ) ) = g ( z ( 3 ) ) h_{\Theta}(x)=a^{(3)}=g(\Theta^{(2)}a^{(2)})=g(z^{(3)}) hΘ(x)=a(3)=g(Θ(2)a(2))=g(z(3))
则有:
z i ( j ) = Θ i , 0 ( j − 1 ) a 0 ( j − 1 ) + Θ i , 1 ( j − 1 ) a 0 ( j − 1 ) + ⋯ + Θ i , n ( j − 1 ) a n ( j − 1 ) z_i^{(j)}=\Theta_{i,0}^{(j-1)}a_0^{(j-1)}+\Theta_{i,1}^{(j-1)}a_0^{(j-1)}+\cdots+\Theta_{i,n}^{(j-1)}a_n^{(j-1)} zi(j)=Θi,0(j−1)a0(j−1)+Θi,1(j−1)a0(j−1)+⋯+Θi,n(j−1)an(j−1)
z ( j ) = Θ ( j − 1 ) a ( j − 1 ) , a ( j ) = g ( z ( j ) ) z^{(j)}=\Theta^{(j-1)}a^{(j-1)}\;,\;a^{(j)}=g(z^{(j)}) z(j)=Θ(j−1)a(j−1),a(j)=g(z(j))
通过该式即可计算神经网络中每一层的值。
扩展到所有样本实例:
z ( 2 ) = Θ ( 1 ) X T z^{(2)}=\Theta^{(1)}X^T z(2)=Θ(1)XT
这时 z ( 2 ) z^{(2)} z(2)是一个 s 2 × m s_2\times m s2×m维的矩阵。
其中各个字母的代表意思维:
m :训练集中的样本实例数量 m:训练集中的样本实例数量 m:训练集中的样本实例数量
s 2 :第二层神经网络中激活单元的数量 s_2:第二层神经网络中激活单元的数量 s2:第二层神经网络中激活单元的数量