R语言相关性分析与偏相关分析

原始数据：

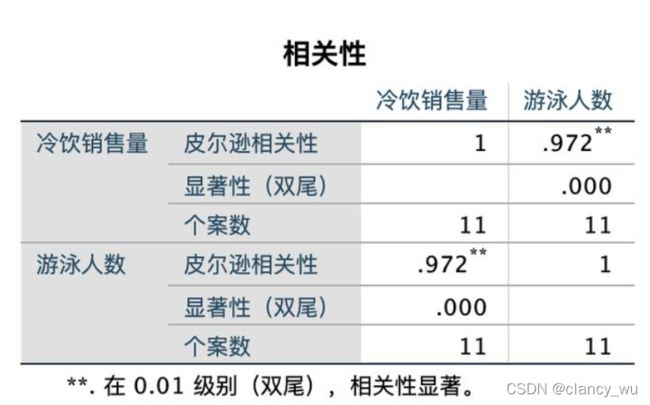
结果


用R实现：
统计学里，比较重要的方法，一个是协方差分析，另一个就是偏相关分析了。
协方差分析，就是在回归分析的基础上进行建模，找出去除混杂变量后，两个变量是否有显著关系，在R语言中公式如下：

summary(aov(y ~ x1+x2)) # x1是混淆变量，x2是组别。

相关性分析的原理也很简单，就是用y~x建立一元回归模型f(x)，然后用实际的x减去模型预测的x，再根据差值分布求得p值。
偏相关分析的原理：

如上图，如果我们想考察X1和X2的偏相关系数，控制变量为z1, z2, z3…（所以控制变量可以是多个）。
首先，分别以X1和X2为因变量，以z1, z2, z3…为自变量，做多重线性回归（后面我们会详细讲解线性回归的内容），获得X1和X2的预测值（“^”表示预测值的意思，一般读作“hat”）；
然后，分别计算残差（实际值-预测值），再对所得到的残差计算Pearson相关系数，结果即为X1和X2的偏相关系数。
逻辑很简单，总结而言，就是“先回归、求残差、再相关”。

R语言实现：

可以看出，spss算出来的皮尔逊相关系数 r 是0.972，p值=0.000，
用R的cor.test( )算出来的是cor=0.9723924，p值=0.000，跟spss一模一样。
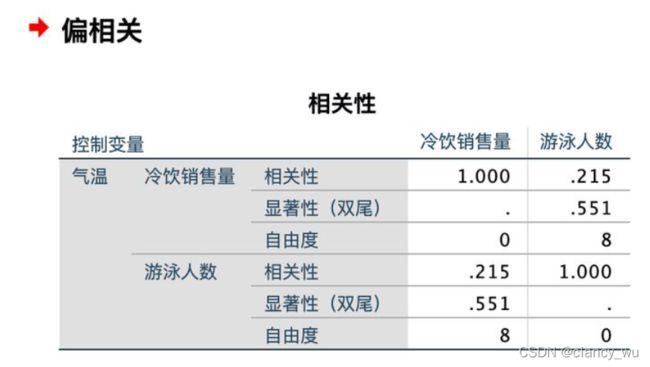
接下来计算偏相关分析：
使用ggm包的pcor.test
pcor.test（）

usage: pcor.test(r, q, n)
r : a partial correlation coefficient, computed by pcor. #pcor的结果
q ：the number of variables in the conditioning set. #条件集个数
n ：integer > 0, the sample size. # 样本量
结果：
tval ： The Student’s t-test statistic.
df ： The degrees of freedom
pvalue ： The P-value, assuming a two-sided alternative.

pcor（）

usage: pcor(u, S)
u是指定的要计算其相关性的变量的指数
S是样本的协方差矩阵

具体到这个数据，S就是cov(data)，然后u就是c(1,2,3)，这样就是冷饮销量与游泳的偏相关。如果是c(1,3,2)，那就是冷饮与气温的偏相关。总之1和2必须是要计算相关性的两个变量的矩阵位置。
代码如下：

pcor.test(pcor(c(1,2,3), cov(data)), 1,11)

可以看到，pvalue是0.551，自由度是8，和spss一样，不过没有看到相关系数rho，这就很难受了。

还有另一种更好的实现方法，就是ppcor包的pcor（）。

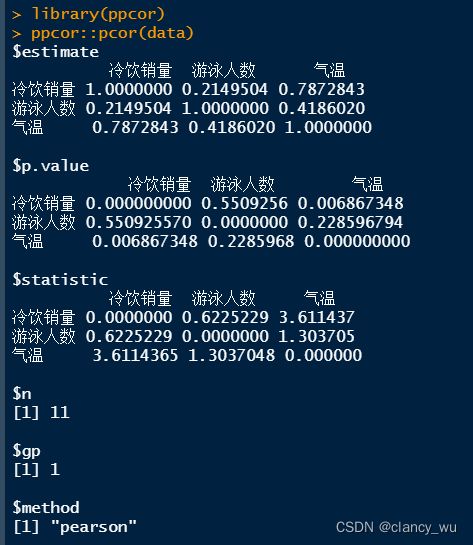
可以看到，ppcor::pcor可以直接输出数据框的所有排列组合，我们看冷饮效率对应的游泳人数，它的estimate其实就是估算的r值，也就是0.2149504，因此r=0.2149=0.2150，跟spss一模一样；它的p值是0.5509256，p=0.551跟spss一样，statistic就是t值，t=0.6225229和前面的一模一样。其余的结果为：n代表样本量11个，gp代表the number of given variables，即条件集的数量，method表示使用的方法，这个是用的和spss差不多的流程自动选择方法，很方便。
所以我还是推荐使用ppcor包，而不要用ggm包，没有R值太难受了。

补充一种更方便的方法：ppcor包的pcor.test（）函数，太绝了！

pcor.test

usage:
pcor.test(x, y, z, method = c(“pearson”, “kendall”, “spearman”))
x : a numeric vector.
y： a numeric vector.
z： a numeric vector.
结果：
estimate ：the partial correlation coefficient between two variables
p.value ：the p value of the test
statistic ：the value of the test statistic
n ：the number of samples
gn ：the number of given variables
method ：the correlation method used

其中要注意的是，多个条件变量的话，需要是一个向量集合，例如下面：

！！！一定要注意的是，使用pcor.test的时候，一定要看清楚自由度n，以及gp值是否正确，尤其是对于两个数据库的调用比较，要使用colbind函数把比较的变量值首先合并再进行pcor.test，不要直接c（），后者会有很明显的代码错误，这个细节很容易被忽视掉。