Kaggle练习赛Spaceship Titantic数据探索(上)
Kaggle练习赛Spaceship Titantic数据探索(上)
kaggle上的练习赛,自己对训练集数据做的一个简单的数据探索。
网址
数据特征描述:
PassengerId- 每位乘客的唯一 ID。
HomePlanet- 乘客离开的星球,通常是他们的永久居住星球。
CryoSleep- 指示乘客是否选择在航程期间进入假死状态。 处于低温睡眠状态的乘客被限制在他们的客舱内。
Cabin- 乘客入住的客舱号码。 采取形式 deck/num/side, 其中 side取值可以是 P或者S,分别对应左舷"P"或右舷"S"。
Destination- 乘客将要去的星球。
Age- 乘客的年龄。
VIP- 旅客在航程中是否支付了VIP服务费用。
RoomService, FoodCourt, ShoppingMall, Spa, VRDeck-在泰坦尼克号宇宙飞船的众多豪华设施中所支付的金额
Name- 乘客的名字和姓氏。
Transported- 乘客是否被运送到另一个维度。 这是要预测的列。
一.对数据正确性进行效验及初步探索。
在了解数据集字段含义后,首先我们需要对数据集的数据质量进行探索,这也是数据探索的最基础的角度。
首先是数据集正确性校验。一般来说数据集正确性校验分为两种,其一是检验数据集字段是否和数据字典中的字段一致,其二则是检验数据集中ID列有无重复。由于该数据集并为提供数据字典,因此此处主要校验数据集ID有无重复:
import pandas as pd
import seaborn as sns
import numpy as np
import matplotlib.pyplot as plt
df = pd.read_csv('train.csv')
#查看乘客ID是否唯一
assert df['PassengerId'].nunique() == df.shape[0]
#查看是否有相同行
assert df.duplicated().sum() == 0
接下来进一步检查数据集缺失情况,可通过自己编写函数来完成。
def missing(df):
'''
计算缺失值比例
'''
missing_number = df.isnull().sum().sort_values(ascending = False)
missing_percent = df.isnull().mean().sort_values(ascending = False)
missing_values = pd.concat([missing_number,missing_percent],axis=1,keys=['missing_number','missing_percent'])
return missing_values
#查看缺失值情况
missing(df)
可以看出缺失值占比并不大,因此可以用一些简单的填补手段进行填补。
二.数据集字段分析
#姓名不好单独编码,需要先处理,构建新的特征姓名长度
df['NameLength'] = df['Name'].str.len()-1
# 将cabin拆分为'Deck', 'Num','Side'三个特征
df[['Deck', 'Num','Side']] = df['Cabin'].str.split('/', expand=True)
#将原来特征抛弃
df = df.drop(['Name','Cabin'],axis = 1)
接下来,我们来标注每一列的数据类型,我们可以通过不同列表来存储不同类型字段的名称:
# 离散字段
category_cols = ['PassengerId', 'HomePlanet', 'CryoSleep', 'Destination', 'VIP', 'Deck',
'Num', 'Side'] + ['NameLength'] +['Age']
# 标签
target = 'Transported'
# 连续字段
numeric_cols = ['RoomService','FoodCourt','ShoppingMall','Spa','VRDeck']
# 验证是否划分能完全
assert len(category_cols) + len(numeric_cols) + 1 == df.shape[1]
#将所有连续字段转化为浮点数,同时如果有空字符将会转化为np.nan
for col in numeric_cols:
df[col]= df[col].apply(lambda x: x if x!= ' ' else np.nan).astype(float)
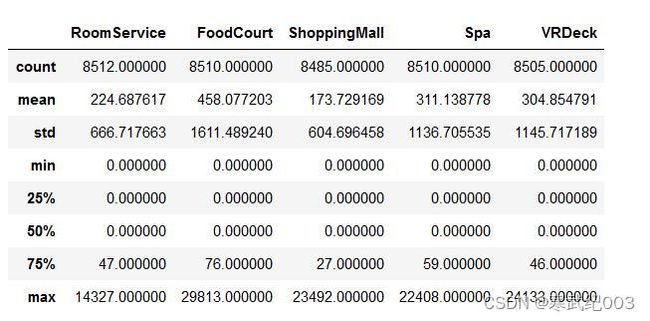
当然,对于连续型变量,我们可以进一步对其进行异常值检测。首先我们可以采用describe方法整体查看连续变量基本统计结果:
df[numeric_cols].describe()
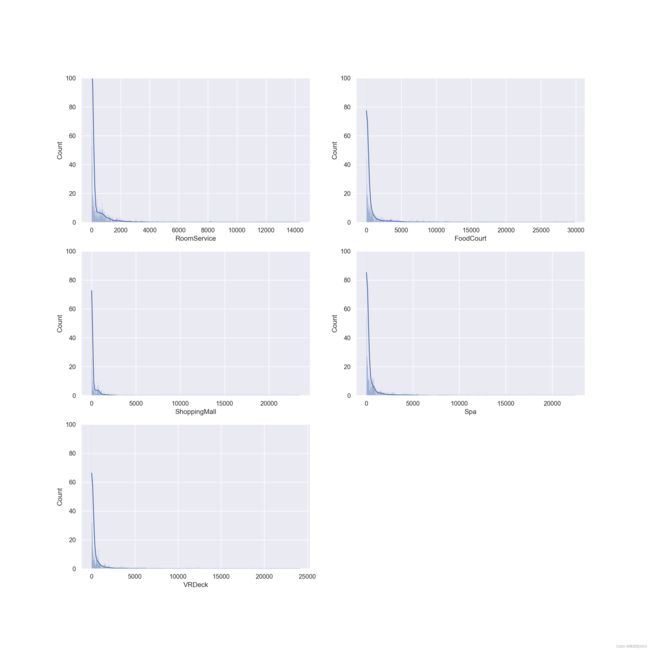
结果出乎意料,大部分人都没有消费。为进一步观察数据,可画出频率分布直方图。
plt.figure(figsize=(16, 16), dpi=200)
for i,col in enumerate(numeric_cols):
plt.subplot(3,2,i+1)
sns.histplot(df[col], kde=True).set_ylim(0,100)
异常值检测有很多方法,我们可以通过三倍标准差法来进行检验,即以均值-3倍标注差为下界,均值+3倍标准差为上界,来检测是否有超过边界的点。此外,我们还可以通过箱线图来进行异常值点的识别,和3倍标准差法利用均值和方差进行计算不同,箱线图主要借助中位数和四分位数来进行计算,以上四分位数+1.5倍四分位距为上界、下四分位数-1.5倍四分位距为下界,超出界限则认为是异常值。
由图可知并不符合正态分布,因此箱线图来进行异常值点的识别。
for col in numeric_cols:
Q3 = df[numeric_cols].describe()[col]['75%']
Q1 = df[numeric_cols].describe()[col]['25%']
IQR = Q3 - Q1
def get_label(x):
if (Q1 - 1.5 * IQR) < x < (Q3 + 1.5 * IQR):
return 1
if np.isnan(x):
return np.nan
else:
return 0
df[col] = df[col].apply(get_label) #这里我是将原有特征顶替,同时将异常值标记为1
for col in df.columns.to_list():
df[col].fillna(df[col].mode()[0], inplace=True)#众数填充,因为连续值被离散化了
三.数据重编码.
考虑到Onehot编码带来的哑变量过多,不利于接下来分析,因此选择OrdinalEncoder自然数排序。
cate = ['HomePlanet', 'Destination', 'Deck', 'Num', 'Side']#剩余的object特征
from sklearn import preprocessing
# 实例化转化器
enc = preprocessing.OrdinalEncoder()
enc.fit(df[cate])
df[cate] = enc.transform(df[cate])
四.变量相关性分析.
接下来,我们尝试对变量和标签进行相关性分析。从严格的统计学意义讲,不同类型变量的相关性需要采用不同的分析方法,例如连续变量之间相关性可以使用皮尔逊相关系数进行计算,而连续变量和离散变量之间相关性则可以卡方检验进行分析,而离散变量之间则可以从信息增益角度入手进行分析。但是,如果我们只是想初步探查变量之间是否存在相关关系,则可以忽略变量连续/离散特性,统一使用相关系数进行计算,这也是pandas中的.corr方法所采用的策略。
# 剔除ID列
df3 = df.iloc[:,1:].copy()
#绘制热力图
plt.figure(figsize=(15,8), dpi=200)
sns.heatmap (df3.corr())
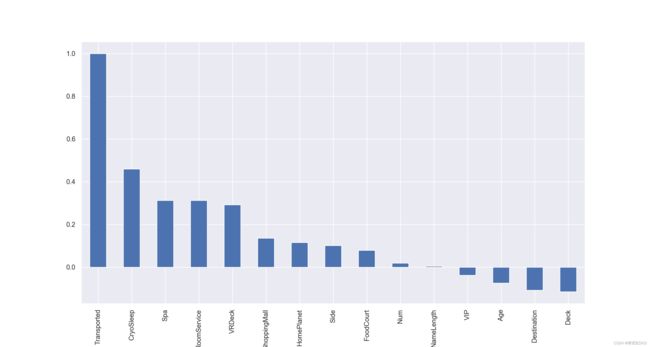
当然,很多时候如果特征较多,热力图的展示结果并不直观,此时我们可以考虑进一步使用柱状图来进行表示:
sns.set()
plt.figure(figsize=(15,8), dpi=200)
df3.corr()[target].sort_values(ascending = False).plot(kind='bar')
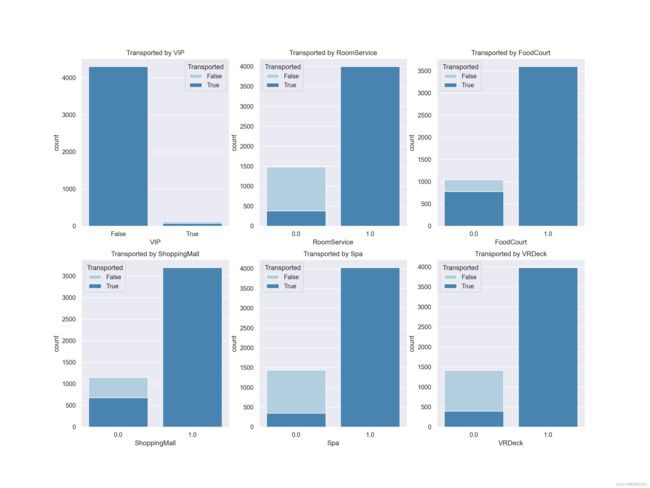
当然,直接计算整体相关系数矩阵以及对整体相关性进行可视化展示是一种非常高效便捷的方式,在实际的算法竞赛中,我们也往往会采用上述方法快速的完成数据相关性检验和探索工作。不过,如果是对于业务分析人员,可能我们需要为其展示更为直观和具体的一些结果,才能有效帮助业务人员对相关性进行判别。此时我们可以考虑围绕不同类型的属性进行柱状图的展示与分析。,因此可以考虑使用柱状图的另一种变形:堆叠柱状图来进行可视化展示:
col_1 = ['VIP','RoomService','FoodCourt','ShoppingMall','Spa','VRDeck',]
fig,axes=plt.subplots(nrows=2,ncols=3,figsize=(16,12), dpi=200)
for i, item in enumerate(col_1):
plt.subplot(2,3,(i+1))
ax=sns.countplot(x=item,hue=target,data=df,palette="Blues", dodge=False)
plt.xlabel(item)
plt.title("Transported by "+ item)
观察堆叠柱状图发现之前被标记为1的特征都到达了另一个维度,这也间接证明之前的标记是有用的。