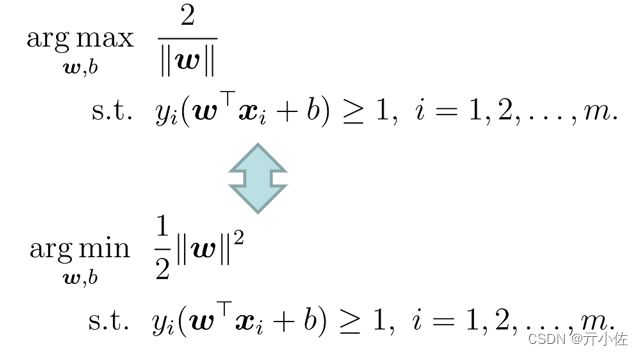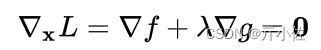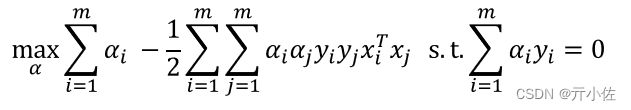机器学习——支持向量机SVM

SVM简介

支持向量机（support vector machines, SVM）是一种二分类模型，它的基本模型是定义在特征空间上的间隔最大的线性分类器，间隔最大使它有别于感知机；SVM还包括核技巧，这使它成为实质上的非线性分类器。SVM的的学习策略就是间隔最大化，可形式化为一个求解凸二次规划的问题，也等价于正则化的合页损失函数的最小化问题。SVM的的学习算法就是求解凸二次规划的最优化算法。

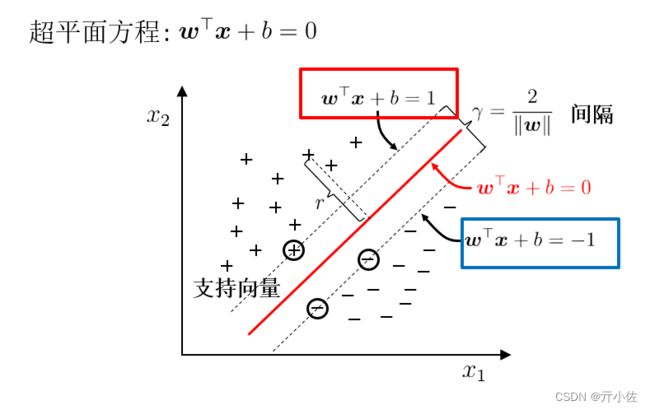
最大间隔与分类：

原理举例：wT取（w1,w2），x取（x1,x2）T， 则原式得 w1x1+w2x2+b=0 与传统直线 Ax+By+c=0 方程式
相同，由二维三维空间推到更高维平面的一般式即为上式。
W：为平面法向量，决定了超平面的方向
b: 决定了超平面距原点的距离
法向量与样本属性的个数、超空间维数相同。在超空间中我们要求的参数就是决定超平面的W和b值。

如图所示：                                                                             

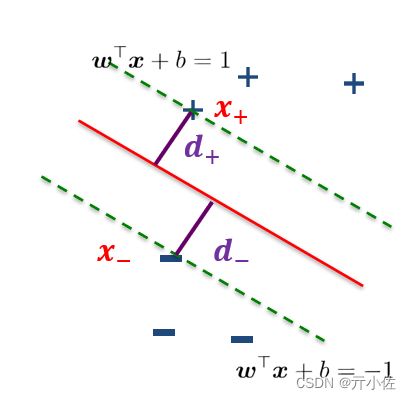
令 +和 - 位于决策边界上，标签分别为正、负的两个样本，考虑 +x_ 到分类线的距离为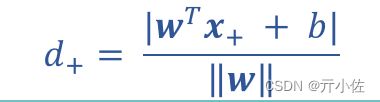
因此，分类间隔为：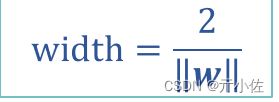

最大化间隔：寻找参数w和b，使得下述公式最大

间隔最大化例子：

 对偶问题：

等式约束：

给定一个目标函数 f : Rn→R，希望找到x∈Rn，在满足约束条件g(x)=0的前提下，使得f(x)有最小值。该约束优化问题记为：

可建立拉格朗日函数：

其中 λ 称为拉格朗日乘数。因此，可将原本的约束优化问题转换成等价的无约束优化问题：

 分别对待求解参数求偏导，可得：

 一般联立方程组可以得到相应的解。

 不等式约束的KKT条件：

将约束等式 g(x)=0 推广为不等式 g(x)≤0。这个约束优化问题可改为：

同理，其拉格朗日函数为：

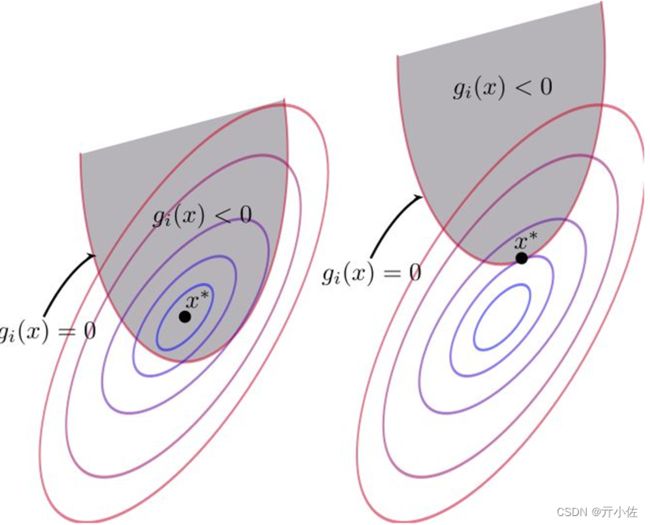
拉格朗日乘子法的几何意义即在等式g(x)=0或在不等式约束g(x)≤0下最小化目标函数f(x)，如下图：

①当 g(x)＜0 时：对f(x)求极值相当于闭区间求极值，最值点即为极值点，令λ=0，直接对f求梯度即可得到极值。

②当 g(x) = 0 时：说明极值点在边界取到，即g(x)＜0内的点值都大于边界，梯度的定义是向函数值增加最快的方向，所以f的梯度与g的梯度相反，从而存在常数λ＞0，使得：

其约束范围为不等式，因此可等价转化成Karush-Kuhn-Tucker (KKT)条件：

 在此基础上，通过优化方式（如二次规划或SMO）求解其最优解。

SMO算法：

SMO算法工作原理是：每次循环中选择两个α进行优化处理。一旦找到一对合适的α，那么就增大其中一个同时减小另一个。这里所谓的“合适”就是指两个α必须要符合 一定的条件，条件之一就是这两个α必须要在间隔边界之外，而其第二个条件则是这两个α还没有进行过区间化处理或者不在边界上

来到SVM的对偶问题上

基本思路：不断执行如下两个步骤直至收敛

偏移项b：通过支持向量来确定

代码实现：

数据集采用网上寻找的ris鸢尾花数据集，它包含3个不同品种的鸢尾花：[Setosa，Versicolour，and Virginica]数据，特征：[‘sepal length’, ‘sepal width’, ‘petal length’, ‘petal width’],一共150个数据。

import numpy as np
import pandas as pd
from sklearn.datasets import load_iris
from sklearn.model_selection import  train_test_split
import matplotlib.pyplot as plt

#加载数据
def create_data():
    iris = load_iris()
    #选取前两类作为数据
    Data=np.array(iris["data"])[:100]
    Label=np.array(iris["target"])[:100]
    Label=Label*2-1
    print("dara shape:",Data.shape)
    print("label shape:",Label.shape)
    return Data, Label

class SVM:
    def __init__(self, max_iter=100, kernel='linear'):
        self.max_iter = max_iter
        self._kernel = kernel

    #参数初始化
    def init_args(self, features, labels):
        self.m, self.n = features.shape
        self.X = features
        self.Y = labels
        self.b = 0.0
        self.alpha = np.ones(self.m)
        self.computer_product_matrix()#为了加快训练速度创建一个内积矩阵
        # 松弛变量
        self.C = 1.0
        # 将Ei保存在一个列表里
        self.create_E()

    #KKT条件判断
    def judge_KKT(self, i):
        y_g = self.function_g(i) * self.Y[i]
        if self.alpha[i] == 0:
            return y_g >= 1
        elif 0 < self.alpha[i] < self.C:
            return y_g == 1
        else:
            return y_g <= 1

    #计算内积矩阵#如果数据量较大，可以使用系数矩阵
    def computer_product_matrix(self):
        self.product_matrix = np.zeros((self.m,self.m)).astype(np.float)
        for i in range(self.m):
            for j in range(self.m):
                if self.product_matrix[i][j]==0.0:
                    self.product_matrix[i][j]=self.product_matrix[j][i]= self.kernel(self.X[i], self.X[j])

    # 核函数
    def kernel(self, x1, x2):
        if self._kernel == 'linear':
            return np.dot(x1,x2)
        elif self._kernel == 'poly':
            return (np.dot(x1,x2) + 1) ** 2
        return 0

    #将Ei保存在一个列表里
    def create_E(self):
        self.E=(np.dot((self.alpha * self.Y),self.product_matrix)+self.b)-self.Y

    # 预测函数g(x)
    def function_g(self, i):
        return self.b+np.dot((self.alpha * self.Y),self.product_matrix[i])

    #选择变量
    def select_alpha(self):
        # 外层循环首先遍历所有满足0= 0:
                j =np.argmin(self.E)
            else:
                j = np.argmax(self.E)
            return i, j

    #剪切
    def clip_alpha(self, _alpha, L, H):
        if _alpha > H:
            return H
        elif _alpha < L:
            return L
        else:
            return _alpha
    #训练函数，使用SMO算法
    def Train(self, features, labels):
        self.init_args(features, labels)
        #SMO算法训练
        for t in range(self.max_iter):
            i1, i2 = self.select_alpha()

            # 边界
            if self.Y[i1] == self.Y[i2]:
                L = max(0, self.alpha[i1] + self.alpha[i2] - self.C)
                H = min(self.C, self.alpha[i1] + self.alpha[i2])
            else:
                L = max(0, self.alpha[i2] - self.alpha[i1])
                H = min(self.C, self.C + self.alpha[i2] - self.alpha[i1])

            E1 = self.E[i1]
            E2 = self.E[i2]
            # eta=K11+K22-2K12
            eta = self.kernel(self.X[i1], self.X[i1]) + self.kernel(self.X[i2], self.X[i2]) - 2 * self.kernel(
                self.X[i1], self.X[i2])
            if eta <= 0:
                # print('eta <= 0')
                continue

            alpha2_new_unc = self.alpha[i2] + self.Y[i2] * (E1 - E2) / eta  # 此处有修改，根据书上应该是E1 - E2，书上130-131页
            alpha2_new = self.clip_alpha(alpha2_new_unc, L, H)

            alpha1_new = self.alpha[i1] + self.Y[i1] * self.Y[i2] * (self.alpha[i2] - alpha2_new)

            b1_new = -E1 - self.Y[i1] * self.kernel(self.X[i1], self.X[i1]) * (alpha1_new - self.alpha[i1]) - self.Y[
                i2] * self.kernel(self.X[i2], self.X[i1]) * (alpha2_new - self.alpha[i2]) + self.b
            b2_new = -E2 - self.Y[i1] * self.kernel(self.X[i1], self.X[i2]) * (alpha1_new - self.alpha[i1]) - self.Y[
                i2] * self.kernel(self.X[i2], self.X[i2]) * (alpha2_new - self.alpha[i2]) + self.b

            if 0 < alpha1_new < self.C:
                b_new = b1_new
            elif 0 < alpha2_new < self.C:
                b_new = b2_new
            else:
                # 选择中点
                b_new = (b1_new + b2_new) / 2

            # 更新参数
            self.alpha[i1] = alpha1_new
            self.alpha[i2] = alpha2_new
            self.b = b_new

            self.create_E()#这里与书上不同，，我选择更新全部E

    def predict(self, data):
        r = self.b
        for i in range(self.m):
            r += self.alpha[i] * self.Y[i] * self.kernel(data, self.X[i])

        return 1 if r > 0 else -1

    def score(self, X_test, y_test):
        right_count = 0
        for i in range(len(X_test)):
            result = self.predict(X_test[i])
            if result == y_test[i]:
                right_count += 1
        return right_count / len(X_test)

if __name__ == '__main__':
    svm = SVM(max_iter=200)
    X, y = create_data()
    X_train, X_test, y_train, y_test = train_test_split( X, y, test_size=0.333, random_state=23323)
    svm.Train(X_train, y_train)
    print(svm.score(X_test, y_test))

结果截图：