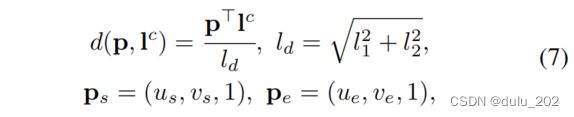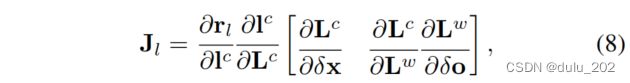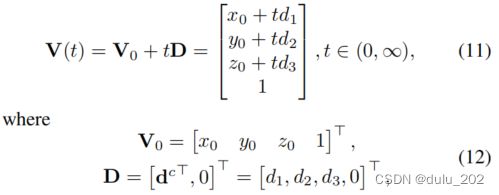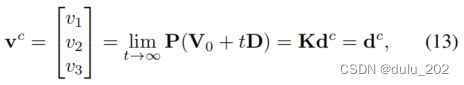【论文精读】UV-SLAM: Unconstrained Line-based SLAM Using Vanishing Points for Structural Mapping

【论文精读】UV-SLAM: Unconstrained Line-based SLAM Using Vanishing Points for Structural Mapping

论文出处

ICRA 2022

摘要

在基于特征的SLAM中，线特征补充了点特征的稀疏性，使得绘制周围的环境结构成为可能。现有的利用线特征的方法主要采用了一种使用线重投影的测量模型。然而，因为线测量模型只使用普吕克坐标系下的线法向量，所以在3D线建图过程中使用的方向向量不能修正。因此，在3D线建图过程中出现的退化问题无法解决。为了解决这一问题，本文提出了一种UV-SLAM，这是一种使用消失点的无约束基于线的SLAM。本文着重于使用没有任何约束的结构规律，如曼哈顿世界假设。为此，我们使用可以从线特征中得到的消失点。将通过图像中的线特征计算出的消失点观测与通过方向向量计算出的消失点估计之间的差值定义为残差，并添加到基于优化的SLAM的代价函数中。此外，通过对Fisher信息矩阵秩的分析，我们证明了消失点测量保证了一个唯一的地图解。最后，我们证明了与使用公共数据集的最先进的算法相比，定位精度和地图质量都得到了提高。

贡献

• 据我们所知，所提出的UV-SLAM是第一个基于优化的单目SLAM，使用消失点测量进行结构建图，不受任何限制，如相机运动和环境。特别是，我们的算法在提取消失点并将它们作为测量的过程中没有使用曼哈顿世界假设。
• 基于最常用的表达3D线特征的方法：普吕克坐标系和正交表示法，我们定义了一个新的消失点测量的残差项和雅可比矩阵。
• 通过Fisher信息矩阵（FIM)秩分析，证明了该方法保证了3D线的可观性，通过此方法，解决了线特征在3D建图出现的问题。

方法

A. 算法框架

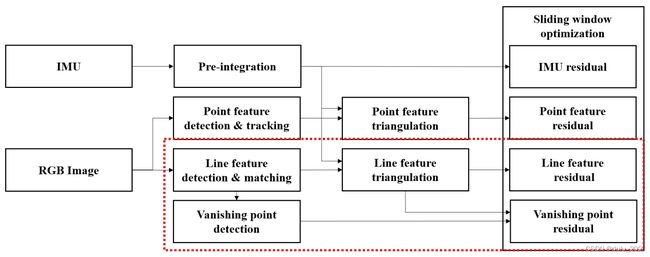当接收到RGB图像时，进行线特征的检测和匹配，然后检测消失点，并对每一条线进行聚类。在通过三角测量线程创建3D线后，线和消失点的残差被定义出来。最后，通过滑动窗口优化可以得到定位和建图的结果。

该方法基于VINS-Mono，IMU和点测量的方法与之相似。点特征从Shi-Tomasi中提取，并由KLT进行跟踪。此外，IMU的测量模型被定义为预积分方法。最后，我们基于优化的方法采用Schur补的双重边缘化。为了将线特征添加到VIO系统中，采用LSD提取线特征，并通过LBD进行跟踪。3D点可以用$（x,y,z)$直观表示，3D线用普吕克坐标系和标准正交法来表示。普吕克坐标系是一种表示3D线的直观方式，一个3D线被表示为：
$$L(n,d{)}^T\in R^6$$

其中，$n$和$d$分别表示法向量和方向向量。普吕克坐标系用于三角测量和重投影过程。而3D线实际上是4-DoF，在普吕克坐标下却是6-DoF。因此，在VIO或视觉SLAM的优化过程中会出现过参（over-parameterization）的问题。为了解决这个问题，采用了正交表示法，用4-DoF表示线。用于优化过程中的线可表示为：
$$o=[\psi ,\varphi ]$$

其中$\psi$是3D线相对于相机坐标系的欧拉角表示的旋转矩阵，$\varphi$是表示相机中心到该直线最小距离的参数。

另外，UV-SLAM还可以确定提取到的直线是否具有结构规律。对于消失点的检测，提出的算法使用J-linkage，可以在存在噪声和异常值的情况下找到多个实例。整个过程如下：首先，通过对图像中提取到的所有直线进行随机采样，创建消失点假设。然后，通过比较不同假设，合并相似的消失点，计算出消失点。由于J-linkage可以通过假设找到所有可能的消失点，它可以比带有曼哈顿世界假设的其他算法找到更多的消失点。

B. 状态定义

$(\cdot {)}^w$，$(\cdot {)}^c$，$(\cdot {)}^b$分别表示世界坐标系、相机坐标系和body坐标系，此外，$(\cdot {)}_b^w$表示body坐标系到世界坐标系的旋转矩阵，四元数或平移的坐标变换。系统中的状态向量如下：
$$\begin{gathered} \mathcal{X}=[{\mathbf{x}}_0,{\mathbf{x}}_1,\dots ,{\mathbf{x}}_{I-1},{\lambda }_0,{\lambda }_1,\dots ,{\lambda }_{J-1},{\mathbf{o}}_0,{\mathbf{o}}_1,\dots ,{\mathbf{o}}_{K-1}] \\ {\mathbf{x}}_i=\left[{\mathbf{p}}_{b_i}^w,{\mathbf{q}}_{b_i}^w,{\mathbf{v}}_{b_i}^w,{\mathbf{b}}_a,{\mathbf{b}}_g\right],i\in [0,I-1] \\ {\mathbf{o}}_k=\left[{\psi }_k,{\varphi }_k\right],k\in [0,K-1] \end{gathered}$$

其中，$\mathcal{X}$表示系统整个状态量，${\mathbf{x}}_i$表示第$i$个滑动窗口的imu的状态量，包括位置，四元数旋转，速度，加速度计和陀螺仪的偏差。另外，整个状态还包括点特征的逆深度，被表示为${\lambda }_j，j\in [0,J-1]$。用正交表示法表示的线被定义为$o$，$I，J，K$分别为滑动窗口，点特征和线特征的个数。

C. UV-SLAM

优化的整个目标函数如下：
${\min }_{\mathcal{X}}\left\{\Vert r_0-J_0\mathcal{X}{\Vert }^2+{\sum }_{i\in \mathcal{B}}\Vert r_I({\mathbf{z}}_{b_i+1}^{b_i},\mathcal{X}){\Vert }_{{\sum }_{b_{i+1}}^{b_i}}^2+{\sum }_{(i,j)\in \mathcal{P}}{\rho }_p\Vert r_p({\mathbf{z}}_{p_j}^{c_i},\mathcal{X}){\Vert }_{{\sum }_{p_j}^{c_i}}^2+{\sum }_{(i,k)\in \mathcal{L}}{\rho }_l\Vert r_l({\mathbf{z}}_{l_k}^{c_i},\mathcal{X}){\Vert }_{{\sum }_{l_k}^{c_i}}^2+{\sum }_{(i,k)\in \mathcal{V}}{\rho }_v\Vert r_v({\mathbf{z}}_{v_k}^{c_i},\mathcal{X}){\Vert }_{{\sum }_{v_k}^{c_i}}^2\right\}$

其中，$r_0，r_I，r_p，r_l，r_v$分别表示边缘化，IMU，点，线和消失点的测量残差。另外，$z_{b_{i+1}}^{b_i}，z_{p_j}^{c_i}，z_{l_k}^{c_i}，z_{v_k}^{c_i}$分别表示对IMU，点，线和消失点的观测，$\mathcal{B}$是一个滑动窗口中所有IMU测量值预积分的集合，$\mathcal{P}，\mathcal{L}，\mathcal{V}$是观测帧中点，线，消失点测量值的集合，${\sum }_{b_{i+1}}^{b_i}，{\sum }_{p_j}^{c_i}，{\sum }_{l_k}^{c_i}，{\sum }_{v_k}^{c_i}$分别表示IMU，点，线和消失点测量的协方差矩阵，${\rho }_p，{\rho }_l，{\rho }_v$分别表示IMU，点，线和消失点测量的平均损失函数。${\rho }_p$和${\rho }_l$被设置为Huber范数函数，${\rho }_v$由于消失点测量模型的无界问题被设置为逆切函数。所定义的损失函数的因子图如图所示，如果特定的线没有消失点的测量，则只使用线特征因子作为$o_0$，如果一个特定的线有对应的消失点测量，则使用线特征和消失点因子作为$o_1$。在优化过程中，使用Ceres求解。

对于o0，只有线特征因子用作非结构线，因此，只采用线特征因子，另一方面，o1是一条具有结构规律的线，同时使用线特征因子和消失点因子

D. 线的测量模型

首先，3D线$L$在普吕克坐标系下的重投影被定义为：

其中，$l，K^{\prime }，K$各自代表线的重投影，直线特征的投影矩阵，以及相机的内参矩阵。$(f_x,f_y)$和$(c_x,c_y)$分别表示图像的焦距和焦点。由于该算法适用于归一化平面，所以$K$和$K^{\prime }$都是单位矩阵。因此，该方法中的重投影线等价于法向量。

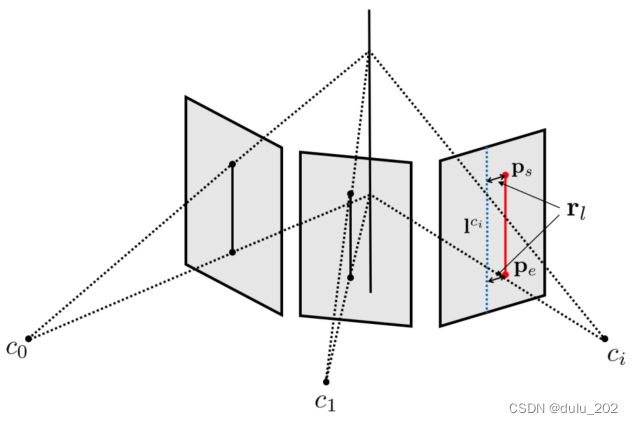
线残差的图例，图像上的红色实线和蓝色虚线分别表示观测和重投影的估计，将三角测量的3D线重投影到新的图像帧中，然后将观测线的两个端点与重投影线之间的距离定义为该线的残差rl。

如图所示，直线测量模型的残差被定义为重投影误差：

其中

$r_l$表示线的残差，$d$表示观测线和重投影线两个端点之间的距离。$P_s$和$P_e$表示图像中观测线的端点。3D线对应的的雅可比矩阵可以用body状态的变化${\delta }_X$和标准正交表示法${\delta }_O$来表示：

其中

其中

${\mathcal{T}}_c^b$是普吕克坐标下相机坐标系到body坐标系的变换矩阵。

E. 消失点测量模型

在计算出消失点后，观测到的线特征利用相应的消失点作为新的观测值。通过消失点对直线聚类如图所示。具有相同消失点的线用相同的颜色表示。

使用消失点聚类线的图像。具有相同消失点的线用相同的颜色表示。通常可以利用J-linkage算法提取出三个或者更多的消失点。

为了估计消失点，3D线上的点用齐次坐标来表示：

$V_0$表示3D线上的点，然后，消失点$V_c$等价于无穷远处的点在3D线上的投影：

其中 $P=K[I|0]$是相机的投影矩阵。在UV-SLAM中，直线上的消失点等价于直线的方向向量。通过$V_c$和图像平面的交集可以计算出消失点的估计，如图所示。最后，消失点的残差被定义为：

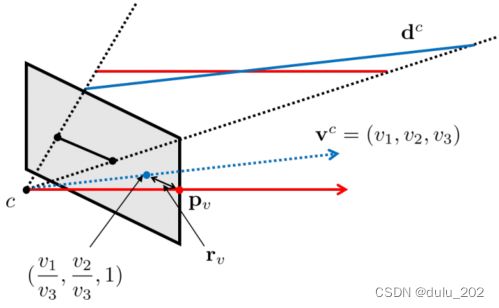
消失点残差的说明，红色实线和蓝色虚线与图像相交的点分别表示消失点的观测和估计。在消失点估计中，使用了直线的方向向量。观测线的观测与3D线估计之间的消失点差被定义为消失点残差。

其中$r_v$和$p_v$分别表示消失点的残差和消失点的观测。用${\delta }_X$和${\delta }_O$可以得到消失点对应的雅可比矩阵如下：

证明

FISHER信息矩阵秩分析

请参考原论文

实验

实验平台：Intel Core i7-9700K处理器，32GB RAM

实验数据集：EuRoC

我们比较了该方法与我们基础算法VINS-Mono的定位精度。此外，我们还比较了PL-VINS、ALVIO和我们之前在VINS-Mono之上使用线特性的工作。比较算法的参数被设置为开源代码中的默认值。我们采用了rpg轨迹评估工具。

由于消失点测量使线特征完全可观测，因此该算法可以得到更准确的结果。

euroc数据集无回环检测的平移RMSE

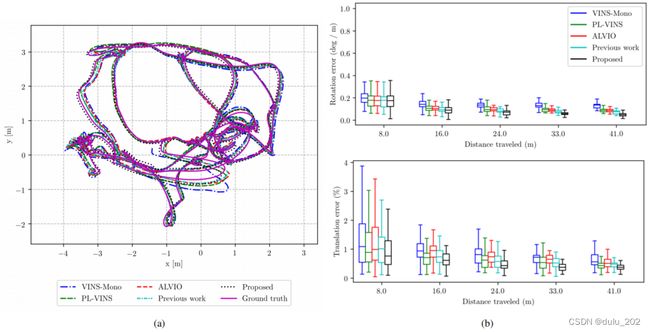
各个算法在euroc数据集V2_02_medium序列的轨迹图和旋转误差、平移误差箱线图的顶视图

EuRoC数据集中MH_05_difficult和V2_01_easy序列a)ALVIO，b)作者之前的工作，c)UV-SLAM建图结果的顶视图

结论

总之，我们提出了UV-SLAM，这是一种使用消失点测量的无约束的基于线的SLAM。所提出的方法可以不需要任何假设而使用，如曼哈顿世界。我们计算了消失点测量的残差矩阵和雅可比矩阵。通过FIM秩的分析，我们在现有方法中引入消失点测量，保证了直线的可观测性。此外，我们还通过与最先进算法的定量和定性比较，发现定位精度和建图质量都得到了提高。对于未来的工作，我们将通过稀疏线地图实现网格或像素级地图。

论文链接

https://arxiv.org/abs/2112.13515