QuadricSLAM
QuadricSLAM论文总结
- 系列文章
- 摘要
- 介绍
- 相关工作
- 对偶二次曲面的基本概念
-
- A.对偶二次曲面
- 对偶二次曲面参数化
- 基于目标检测的传感器模型
- 加入二次曲面后的SLAM
系列文章
1.使用椭球表示物体的语义SLAM的基本知识
2.Semantic SLAM with Autonomous Object-Level Data Association 论文笔记
摘要
本文将2D目标检测的结果融入到SLAM中,使用对偶二次曲面表示物体,作为路标加入到后端中优化物体的位置,尺寸和旋转,形成空间点-相机-物体三者的BA。此外,论文还提出了解决物体部分遮挡的方法。
介绍
传统的视觉SLAM只能够表示几何信息(geometric information),例如点、线和面特征,而无法感知物体级别的语义信息。语义信息丰富的SLAM系统能够提升机器人感知周围环境的能力,提高交互能力等。
接下来就是介绍Quadric二次曲面用于描述物体有什么优点:
- 相对于TSDF,描述物体更加的简单。具有完整的表示。
- 使用椭球表示物体,能够充分表示物体的尺寸、位置和方向
- 在对偶空间中,椭球能够直接从目标检测得到的包围框中生成(这部分在后面会有介绍)
- 博主认为,相对于CubeSLAM使用包围盒描述物体,使用椭球描述物体一个优点是,椭球投影到图像中形成的椭圆是有清晰的数学模型,可以求导用于计算雅可比矩阵。
- 我们率先提出了如何参数化对偶二次曲面作为SLAM中的路标
- 如何将目标检测融入到视觉SLAM中,目标检测的包围框能够直接约束对偶二次曲面的参数。
- 构建基于图优化的SLAM,联合优化机器人位姿和椭球的参数。
- 没有解决物体之间数据关联问题,也就是说它的实验中的物体都是手动标定的。后来的工作,例如EAO-SLAM,就主要专注于解决数据关联问题。
相关工作
就是比较(dui)前人的工作。
对偶二次曲面的基本概念
A.对偶二次曲面
根据之前的讲解,一个对偶二次曲面可以使用4维的方阵 Q ∗ Q^* Q∗来表示。由于是对称矩阵,可以用使用 4 ∗ ( 4 + 1 ) / 2 4*(4+1)/2 4∗(4+1)/2维的向量 q ^ = ( q ^ 1 , q ^ 2 , . . . q ^ 10 ) \hat \bold q=(\hat q_1,\hat q_2, ... \hat q_{10}) q^=(q^1,q^2,...q^10)来表示。由于还有一个尺度因子(右下角的元素),实际上一个对偶二次曲面的自由度为9。
对偶二次曲面参数化
可以将对偶二次曲面参数化为 Q ∗ = Z Q ˇ ∗ Z T (1) Q^* = Z \check Q^*Z^T \tag{1} Q∗=ZQˇ∗ZT(1)
其中 Q ˇ ∗ \check Q^* Qˇ∗表示在原点处的椭球, Z Z Z表示齐次变换矩阵。分别表示为
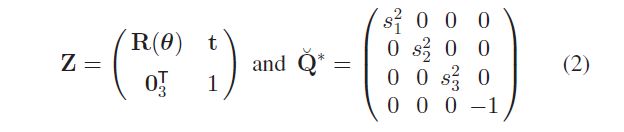
公式(1)可以理解为将椭球由物体坐标系变换到世界坐标系。对于公式(2), t \bold t t表示二次曲面的位置, R ( θ ) R(\bold{\theta}) R(θ)表示旋转矩阵。 θ = ( θ 1 , θ 2 , θ 3 ) \theta =(\theta_1,\theta_2,\theta_3) θ=(θ1,θ2,θ3), s = ( s 1 , s 2 , s 3 ) s=(s_1,s_2,s_3) s=(s1,s2,s3)表示椭球的三个半轴长度。后面,将使用9维的向量 q = ( θ 1 , θ 2 , θ 3 , t 1 , t 2 , t 3 , s 1 , s 2 , s 3 ) \bold q=(\theta_1,\theta_2,\theta_3,t_1,t_2,t_3,s_1,s_2,s_3) q=(θ1,θ2,θ3,t1,t2,t3,s1,s2,s3)来表示。
基于目标检测的传感器模型
这一部分就是讲解如何将带有目标检测信息的图像数据输入到SLAM中。
对于一个2D包围框,可以使用4条线 l k \bold l_k lk或者是一个 b = ( x m i n , y m i n , x m a x , y m a x ) \bold b=(x_{min},y_{min},x_{max},y_{max}) b=(xmin,ymin,xmax,ymax),即左上角和右下角的像素坐标。现在需要构建一个传感器模型 β ( x i , q j ) = b ^ i j \beta(x_i,q_j)=\hat b_{ij} β(xi,qj)=b^ij表示观测值,目标检测的包围框作为预测值,从而构成误差,使用高斯牛顿法,LM算法优化。其中, x i x_i xi表示 i i i时刻相机的位姿, q j q_j qj表示第 j j j个物体, b ^ i j \hat b_{ij} b^ij表示第 i i i时刻看到的第 j j j的物体的在图像中的投影。
上述的 β ( x i , q j ) = b ^ i j \beta(x_i,q_j)=\hat b_{ij} β(xi,qj)=b^ij就是我们在前面所说的椭球的投影,即
C i j ∗ = P i Q ( q j ) ∗ P i T (3) C^*_{ij}=P_iQ^*_{(q_j)}P_i^T\tag{3} Cij∗=PiQ(qj)∗PiT(3)
求 C i j ∗ C^*_{ij} Cij∗的伴随矩阵就可以得到 C i j C_{ij} Cij,进而就可以得到物体的投影矩阵。(在论文中使用BBox表示由 C i j C_{ij} Cij得到包围框)
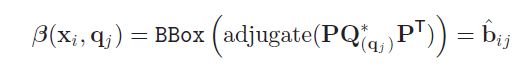
如下图所示,红色是物体投影得到的,蓝色是求出的包围框,黑色是目标检测得到的包围框。然后我们在BA中通过调整相机的位姿和物体的9个参数,使得蓝色和黑色能够拟合。
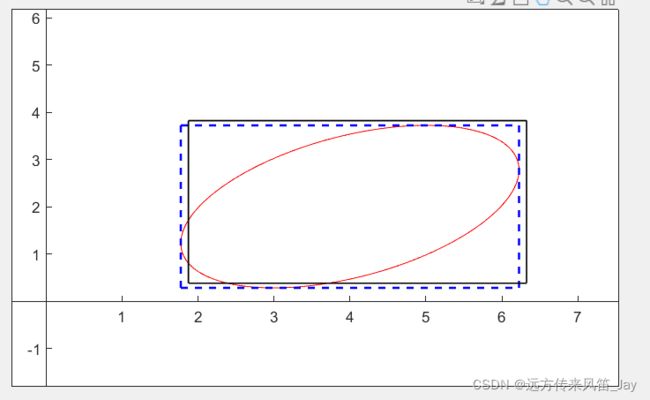
这里贴出上述图像的matlab代码
h = 4;
k = 2;
a = 2.44;
b = 1.4;
alpha = pi/6;
t = -pi:0.01:pi;
% x0 = h + a*b./sqrt( a^2*sin(t).^2 + b^2*cos(t).^2 ).*cos(t);
% y0 = k + a*b./sqrt( a^2*sin(t).^2 + b^2*cos(t).^2 ).*sin(t);
x0 = h + a * cos(t);
y0 = k + b * sin(t);
x = a*cos(t)*cos(alpha) - b*sin(t)*sin(alpha)+h;
y = a*cos(t)*sin(alpha) + b*sin(t)*cos(alpha)+k;
% x = h + a*b./sqrt( a^2*sin(t-alpha).^2 + b^2*cos(t-alpha).^2 ).*cos(t);
% y = k + a*b./sqrt( a^2*sin(t-alpha).^2 + b^2*cos(t-alpha).^2 ).*sin(t);
plot(x,y,'r-','MarkerSize',15);
%条件1:切线l=C(x,y,1)' (x,0,1)*l= 0
%条件2:df/dy = 0
length = sqrt(a*a*cos(alpha)*cos(alpha)+b*b*sin(alpha)*sin(alpha));
width = sqrt(a*a*sin(alpha)*sin(alpha)+b*b*cos(alpha)*cos(alpha));
hold on;
line([-length+h,length+h],[width+k,width+k],'Color','blue','LineStyle','--','LineWidth',1.5);
line([-length+h,length+h],[-width+k,-width+k],'Color','blue','LineStyle','--','LineWidth',1.5);
line([length+h,length+h],[-width+k,width+k],'Color','blue','LineStyle','--','LineWidth',1.5);
line([-length+h,-length+h],[-width+k,width+k],'Color','blue','LineStyle','--','LineWidth',1.5);
delta = 0.1;
line([-length+h+delta,length+h+delta],[width+k+delta,width+k+delta],'Color','black','LineStyle','-','LineWidth',1);
line([-length+h+delta,length+h+delta],[-width+k+delta,-width+k+delta],'Color','black','LineStyle','-','LineWidth',1);
line([length+h+delta,length+h+delta],[-width+k+delta,width+k+delta],'Color','black','LineStyle','-','LineWidth',1);
line([-length+h+delta,-length+h+delta],[-width+k+delta,width+k+delta],'Color','black','LineStyle','-','LineWidth',1);
h = gca;
h.XAxisLocation = 'origin';
h.YAxisLocation = 'origin';
axis([-2,6,-2,6]);
上面程序考虑的是椭球投影后得到的椭圆都在图像平面中,而在程序中考虑到没有全部都在图像中。如下所示,
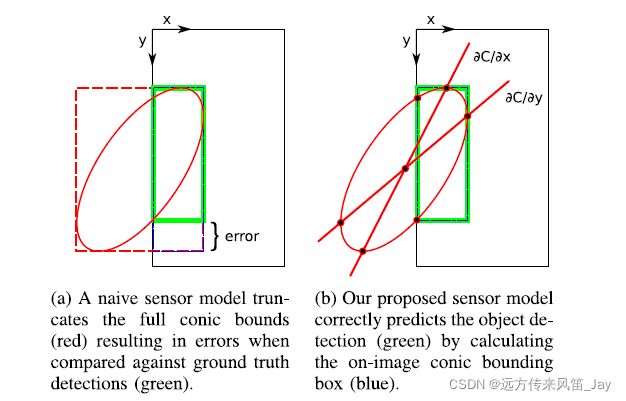
具体的BBox函数过程为
1.搜索x方向和y方向的最大值点和最小值点
2.椭球与物体边界相交的点,至多八个,即图像的 的S4个边都穿过
3.从上述过程得到的点中,剔除non-real的点和在图像外面的点。
4.从剩余点中得到最大和最小x和y的点作为投影包围框。


