Python实现与pytorch实现反向传播的区别
Pytorch 实现反向传播
pytorch是一种深度学习框架,可以使我们方便地进行机器学习方面的研究。例如,求导数是一项很繁琐的过程,而pytorch利用静态计算图已经帮我们自动计算出导数了,这时我们只要调用 backward() 方法就可以自动求导,是不是很方便呢?

全部代码我就不展示了,有点冗余,仅仅展示与 上篇博客 不同之处。
数据点:
输入:(0.5, 0.3) 输出:(0.23, -0.07)初始权值: w1, w2,w3, w4, w5, w6, w7, w8 = [0.2, -0.4, 0.5, 0.6, 0.1, -0.5, -0.3, 0.8]
import torch
def forward_propagate(x1, x2):
in_h1 = w1 * x1 + w3 * x2
out_h1 = sigmoid(in_h1) # out_h1 = torch.sigmoid(in_h1)
in_h2 = w2 * x1 + w4 * x2
out_h2 = sigmoid(in_h2) # out_h2 = torch.sigmoid(in_h2)
in_o1 = w5 * out_h1 + w7 * out_h2
out_o1 = sigmoid(in_o1) # out_o1 = torch.sigmoid(in_o1)
in_o2 = w6 * out_h1 + w8 * out_h2
out_o2 = sigmoid(in_o2) # out_o2 = torch.sigmoid(in_o2)
print("正向计算:o1 ,o2")
print(out_o1.data, out_o2.data)
# 在Python实现前向传播时,将 loss 放入该函数里,而在pytorch实现中是将
# loss 扇出,这么做的原因是降低耦合性,同时也方便更换损失函数来进行对比。
return out_o1, out_o2
def loss_fuction(x1, x2, y1, y2): # 损失函数
y1_pred, y2_pred = forward_propagate(x1, x2) # 前向传播
loss = (1 / 2) * (y1_pred - y1) ** 2 + (1 / 2) * (y2_pred - y2) ** 2 # 考虑 : t.nn.MSELoss()
print("损失函数(均方误差):", loss.item())
return loss
# 由于是自动求导,因此迭代函数需要更换
def update_w(w1, w2, w3, w4, w5, w6, w7, w8):
# 步长
step = 1
w1.data = w1.data - step * w1.grad.data
w2.data = w2.data - step * w2.grad.data
w3.data = w3.data - step * w3.grad.data
w4.data = w4.data - step * w4.grad.data
w5.data = w5.data - step * w5.grad.data
w6.data = w6.data - step * w6.grad.data
w7.data = w7.data - step * w7.grad.data
w8.data = w8.data - step * w8.grad.data
w1.grad.data.zero_() # 注意:将w中所有梯度清零
w2.grad.data.zero_()
w3.grad.data.zero_()
w4.grad.data.zero_()
w5.grad.data.zero_()
w6.grad.data.zero_()
w7.grad.data.zero_()
w8.grad.data.zero_()
return w1, w2, w3, w4, w5, w6, w7, w8
if __name__ == "__main__":
print("=====更新前的权值=====")
print(w1.data, w2.data, w3.data, w4.data, w5.data, w6.data, w7.data, w8.data)
for i in range(1):
print("=====第" + str(i) + "轮=====")
L = loss_fuction(x1, x2, y1, y2) # 前向传播,求 Loss,构建计算图
L.backward() # 自动求梯度,不需要人工编程实现。反向传播,求出计算图中所有梯度存入w中
print("\tgrad W: ", round(w1.grad.item(), 2), round(w2.grad.item(), 2), round(w3.grad.item(), 2),
round(w4.grad.item(), 2), round(w5.grad.item(), 2), round(w6.grad.item(), 2), round(w7.grad.item(), 2),
round(w8.grad.item(), 2))
w1, w2, w3, w4, w5, w6, w7, w8 = update_w(w1, w2, w3, w4, w5, w6, w7, w8)
print("更新后的权值")
print(w1.data, w2.data, w3.data, w4.data, w5.data, w6.data, w7.data, w8.data)
python实现与pytorch实现区别
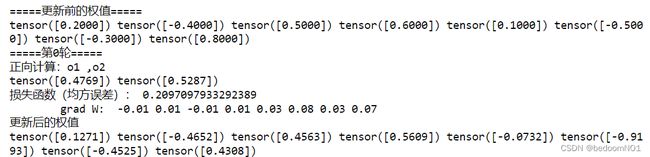
为了验证该实验的正确性,所以进行二者结构对比:
| python实现结果 | pytorch实现结果 |
|---|---|
 |
 |
这时我们会看到二者更新后的权值大相径庭,具体是什么原因导致的呢?比较结果就不难发现,从 grad_W 开始输出结果就不同了。
以w1为例
∂ L ∂ w 1 = ∂ I n h 1 ∂ w 1 ⋅ ∂ O u t h 1 ∂ I n h 1 ⋅ ( ∂ I n o 1 ∂ O u t h 1 ⋅ ∂ O u t o 1 ∂ I n o 1 ⋅ ∂ L ∂ O u t o 1 + ∂ I n o 2 ∂ O u t h 1 ⋅ ∂ O u t o 2 ∂ I n o 2 ⋅ ∂ L ∂ O u t o 2 ) \frac{\partial L}{\partial w_1} =\frac{\partial In_{h1}}{\partial w_1} \cdot\frac{\partial Out_{h1}}{\partial In_{h1}}\cdot(\frac{\partial In_{o1}}{\partial Out_{h1}} \cdot\frac{\partial Out_{o1}}{\partial In_{o1}}\cdot\frac{\partial L}{\partial Out_{o1}}+\frac{\partial In_{o2}}{\partial Out_{h1}} \cdot\frac{\partial Out_{o2}}{\partial In_{o2}}\cdot\frac{\partial L}{\partial Out_{o2}}) ∂w1∂L=∂w1∂Inh1⋅∂Inh1∂Outh1⋅(∂Outh1∂Ino1⋅∂Ino1∂Outo1⋅∂Outo1∂L+∂Outh1∂Ino2⋅∂Ino2∂Outo2⋅∂Outo2∂L)
将数据带入得:
∂ L ∂ w 1 = x 1 ∗ o u t h 1 ∗ ( 1 − o u t h 1 ) ( w 5 ∗ o u t o 1 ∗ ( 1 − o u t o 1 ) ∗ ( o u t o 1 − y 1 ) + w 6 ∗ o u t o 2 ∗ ( 1 − o u t o 2 ) ∗ ( o u t o 2 − y 2 ) ) \frac{\partial L}{\partial w_1} = x_1 * out_{h1} * (1 - out_{h1})(w_5 * out_{o1} * (1 - out_{o1}) * (out_{o1} - y_1)+w_6 * out_{o2} * (1 - out_{o2}) * (out_{o2} - y_2)) ∂w1∂L=x1∗outh1∗(1−outh1)(w5∗outo1∗(1−outo1)∗(outo1−y1)+w6∗outo2∗(1−outo2)∗(outo2−y2))
这时会发现作业二中的错误:

同理,修改所有导数,同时将步长改为1。
def back_propagate(out_o1, out_o2, out_h1, out_h2, w5, w6, w7, w8):
# 反向传播
d_o1 = out_o1 - y1
d_o2 = out_o2 - y2
# print(round(d_o1, 2), round(d_o2, 2))
d_w5 = d_o1 * out_o1 * (1 - out_o1) * out_h1
d_w7 = d_o1 * out_o1 * (1 - out_o1) * out_h2
# print(round(d_w5, 2), round(d_w7, 2))
d_w6 = d_o2 * out_o2 * (1 - out_o2) * out_h1
d_w8 = d_o2 * out_o2 * (1 - out_o2) * out_h2
# print(round(d_w6, 2), round(d_w8, 2))
g_w5 = d_o1 * out_o1 * (1 - out_o1) * w5
g_w6 = d_o2 * out_o2 * (1 - out_o2) * w6
g_w7 = d_o1 * out_o1 * (1 - out_o1) * w7
g_w8 = d_o2 * out_o2 * (1 - out_o2) * w8
d_w1 = (g_w5 + g_w6) * out_h1 * (1 - out_h1) * x1
d_w3 = (g_w5 + g_w6) * out_h1 * (1 - out_h1) * x2
# print(round(d_w1, 2), round(d_w3, 2))
d_w2 = (g_w7 + g_w8) * out_h2 * (1 - out_h2) * x1
d_w4 = (g_w7 + g_w8) * out_h2 * (1 - out_h2) * x2
# print(round(d_w2, 2), round(d_w4, 2))
print("反向传播:误差传给每个权值")
print(round(d_w1, 5), round(d_w2, 5), round(d_w3, 5), round(d_w4, 5), round(d_w5, 5), round(d_w6, 5),
round(d_w7, 5), round(d_w8, 5))
return d_w1, d_w2, d_w3, d_w4, d_w5, d_w6, d_w7, d_w8
def update_w(w1, w2, w3, w4, w5, w6, w7, w8):
# 步长
step = 1
w1 = w1 - step * d_w1
w2 = w2 - step * d_w2
w3 = w3 - step * d_w3
w4 = w4 - step * d_w4
w5 = w5 - step * d_w5
w6 = w6 - step * d_w6
w7 = w7 - step * d_w7
w8 = w8 - step * d_w8
return w1, w2, w3, w4, w5, w6, w7, w8
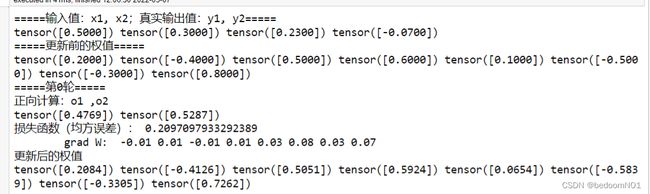
进行比较:
| python实现结果 | pytorch实现结果 |
|---|---|
 |
 |
此时二者输出结果相同。
更换激活函数
torch.sigmoid()
def forward_propagate(x1, x2):
in_h1 = w1 * x1 + w3 * x2
# out_h1 = sigmoid(in_h1) #
out_h1 = torch.sigmoid(in_h1)
in_h2 = w2 * x1 + w4 * x2
# out_h2 = sigmoid(in_h2) #
out_h2 = torch.sigmoid(in_h2)
in_o1 = w5 * out_h1 + w7 * out_h2
# out_o1 = sigmoid(in_o1) #
out_o1 = torch.sigmoid(in_o1)
in_o2 = w6 * out_h1 + w8 * out_h2
# out_o2 = sigmoid(in_o2) #
out_o2 = torch.sigmoid(in_o2)
print("正向计算:o1 ,o2")
print(out_o1.data, out_o2.data)
return out_o1, out_o2
torch.reLu()
def forward_propagate(x1, x2):
in_h1 = w1 * x1 + w3 * x2
# out_h1 = sigmoid(in_h1) #
out_h1 = torch.relu(in_h1)
in_h2 = w2 * x1 + w4 * x2
# out_h2 = sigmoid(in_h2) #
out_h2 = torch.relu(in_h2)
in_o1 = w5 * out_h1 + w7 * out_h2
# out_o1 = sigmoid(in_o1) #
out_o1 = torch.relu(in_o1)
in_o2 = w6 * out_h1 + w8 * out_h2
# out_o2 = sigmoid(in_o2) #
out_o2 = torch.relu(in_o2)
print("正向计算:o1 ,o2")
print(out_o1.data, out_o2.data)
return out_o1, out_o2
更换损失函数
nn.MSELoss()
def loss_fuction(x1, x2, y1, y2): # 损失函数
# y1_pred, y2_pred = forward_propagate(x1, x2) # 前向传播
y_pred = torch.cat(forward_propagate(x1, x2), dim=0)
y = torch.cat((y1, y2), dim=0)
loss = torch.nn.MSELoss(reduction='mean')
l = loss(y_pred, y)
print("损失函数(均方误差):", l.item())
return l
nn.CrossEntropyLoss()
def loss_fuction(x1, x2, y1, y2): # 损失函数
y1_pred, y2_pred = forward_propagate(x1, x2) # 前向传播
y_pred = torch.stack([y1_pred, y2_pred], dim=1) # 将两个预测值放在一个矩阵中
y = torch.stack([y1, y2], dim=1)
loss = torch.nn.CrossEntropyLoss()
l = loss(y_pred, y)
print("损失函数(均方误差):", l.item())
return l
更改步长
| Step | Loss |
|---|---|
| 1 |  |
| 3 |  |
| 5 |  |
| 10 |  |
随着 Iter 的增加,Loss 会递减,而且随着 Step 的增大,Loss 会收敛的更快。
总结
反向传播是深度学习的基础,pytorch内封装了很多基础模块,可以帮助我们更快地实现神经网络,当然对于我这种初学者来说,可能会找不到都函数入口,以至于很多时候都在改变数据类型寻找入口而浪费了很多时间。