数据分析面试【机器学习】总结之-----主要的常见面试题整理（一）

阅读之前看这里：博主是正在学习数据分析的一员，博客记录的是在学习过程中一些总结，也希望和大家一起进步，在记录之时，未免存在很多疏漏和不全，如有问题，还请私聊博主指正。
博客地址：天阑之蓝的博客，学习过程中不免有困难和迷茫，希望大家都能在这学习的过程中肯定自己，超越自己，最终创造自己。

1、过拟合和欠拟合的现象

过拟合：指模型对于训练数据拟合过当的情况，反应到评估指标上，就是模型在训练集上表现很好，但在测试集和新数据集上的表现较差。
欠拟合：指的是模型在训练和预测时表现都不好的情况。

2.造成过拟合和欠拟合的原因，如何解决？

欠拟合的原因：

• 模型复杂度过低
• 特征量过少

解决方法：

1. 增加新特征，可以考虑加入进特征组合、高次特征，来增大假设空间
2. 添加多项式特征，这个在机器学习算法里面用的很普遍，例如将线性模型通过添加二次项或者三次项使模型泛化能力更强（增加模型的复杂度）
3. 减少正则化参数，正则化的目的是用来防止过拟合的，但是模型出现了欠拟合，则需要减少正则化参数
4. 使用非线性模型，比如核SVM、决策树、深度学习等模型
5. 调整模型的容量(capacity)，通俗地，模型的容量是指其拟合各种函数的能力
6. 容量低的模型可能很难拟合训练集；使用集成学习方法，如Bagging ,将多个弱学习器Bagging

过拟合的原因：

• 建模样本选取有误，如样本数量太少，选样方法错误，样本标签错误等，导致选取的样本数据不足以代表预定的分类规则
• 样本噪音干扰过大，使得机器将部分噪音认为是特征从而扰乱了预设的分类规则
• 假设的模型无法合理存在，或者说是假设成立的条件实际并不成立
• 参数太多，模型复杂度过高
• 对于决策树模型，如果我们对于其生长没有合理的限制，其自由生长有可能使节点只包含单纯的事件数据(event)或非事件数据(no event)，使其虽然可以完美匹配（拟合）训练数据，但是无法适应其他数据集
• 对于神经网络模型：a)对样本数据可能存在分类决策面不唯一，随着学习的进行,，BP算法使权值可能收敛过于复杂的决策面；b)权值学习迭代次数足够多(Overtraining)，拟合了训练数据中的噪声和训练样例中没有代表性的特征

过拟合的解决方案

1. 正则化（Regularization）（L1和L2）
2. 数据扩增，即增加训练数据样本
3. Dropout
4. Early stopping

3.什么是正则化，L1和L2正则化的区别

在模型训练的过程中，需要降低 loss 以达到提高 accuracy 的目的。此时，使用正则化之类的方法直接将权值的大小加入到 loss 里，在训练的时候限制权值变大。训练过程需要降低整体的 loss，这时候，一方面能降低实际输出与样本之间的误差，也能降低权值大小。

正则化的主要作用是防止过拟合，对模型添加正则化项可以限制模型的复杂度，使得模型在复杂度和性能达到平衡。

L1正则化和L2正则化可以看做是损失函数的惩罚项。所谓『惩罚』是指对损失函数中的某些参数做一些限制。 L1正则化的模型建叫做Lasso回归，使用L2正则化的模型叫做Ridge回归(岭回归)。

3.1 L1正则化与L2正则化

L1正则化的表达如下，其中$\alpha ||w|{|}_1$为L1正则化项,L1正则化是指权值向量w 中各个元素的绝对值之和。

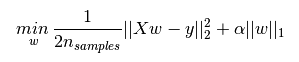
L2正则化项表达式如下，其中$\alpha ||w|{|}_2^2$为L2正则化项，L2正则化是指权值向量w 中各个元素的平方和然后再求平方根。

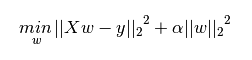
3.2 L1和L2正则化的作用：

• L1正则化可以产生稀疏权值矩阵，即产生一个稀疏模型，可以用于特征选择，一定程度上，L1也可以防止过拟合
• L2正则化可以防止模型过拟合（overfitting）
• L2正则化可以直观理解为它对于大数值的权重向量进行严厉惩罚，倾向于更加分散的权重向量。由于输入和权重之间的乘法操作，这样就有了一个优良的特性：使网络更倾向于使用所有输入特征，而不是严重依赖输入特征中某些小部分特征。
  L2惩罚倾向于更小更分散的权重向量，这就会鼓励分类器最终将所有维度上的特征都用起来，而不是强烈依赖其中少数几个维度。这样做可以提高模型的泛化能力，降低过拟合的风险。
• L1正则化有一个有趣的性质，它会让权重向量在最优化的过程中变得稀疏（即非常接近0）。也就是说，使用L1正则化的神经元最后使用的是它们最重要的输入数据的稀疏子集，同时对于噪音输入则几乎是不变的了。相较L1正则化，L2正则化中的权重向量大多是分散的小数字。

3.3 小结

1. 添加正则化相当于参数的解空间添加了约束，限制了模型的复杂度
2. L1正则化的形式是添加参数的绝对值之和作为结构风险项，L2正则化的形式添加参数的平方和作为结构风险项
3. L1正则化鼓励产生稀疏的权重，即使得一部分权重为0，用于特征选择；L2鼓励产生小而分散的权重，鼓励让模型做决策的时候考虑更多的特征，而不是仅仅依赖强依赖某几个特征，可以增强模型的泛化能力，防止过拟合。
4. 正则化参数 λ越大，约束越严格，太大容易产生欠拟合。正则化参数 λ越小，约束宽松，太小起不到约束作用，容易产生过拟合。
5. 如果不是为了进行特征选择，一般使用L2正则化模型效果更好。

4.过拟合的其它解决方案

数据扩增

这是解决过拟合最有效的方法，只要给足够多的数据，让模型「看见」尽可能多的「例外情况」，它就会不断修正自己，从而得到更好的结果。

如何获取更多数据，可以有以下几个方法

1. 从数据源头获取更多数据
2. 根据当前数据集估计数据分布参数，使用该分布产生更多数据：这个一般不用，因为估计分布参数的过程也会代入抽样误差
3. 数据增强（Data Augmentation）：通过一定规则扩充数据。如在物体分类问题里，物体在图像中的位置、姿态、尺度，整体图片明暗度等都不会影响分类结果。我们就可以通过图像平移、翻转、缩放、切割等手段将数据库成倍扩充

Dropout

在训练时，每次随机（如50%概率）忽略隐层的某些节点；这样，我们相当于随机从 2n(n个神经元的网络) 个模型中采样选择模型

Early stopping

Early stopping便是一种迭代次数截断的方法来防止过拟合的方法，即在模型对训练数据集迭代收敛之前停止迭代来防止过拟合。
具体做法是，在每一个Epoch结束时计算validation data的accuracy，当accuracy不再提高时，就停止训练。当然我们并不会在accuracy一降低的时候就停止训练，因为可能经过这个Epoch后，accuracy降低了，但是随后的Epoch又让accuracy又上去了，所以不能根据一两次的连续降低就判断不再提高。一般的做法是，在训练的过程中，记录到目前为止最好的validation accuracy，当连续10次Epoch（或者更多次）没达到最佳accuracy时，则可以认为accuracy不再提高了。此时便可以停止迭代了（Early Stopping）。这种策略也称为“No-improvement-in-n”，n即Epoch的次数，可以根据实际情况取，如10、20、30……

5.超参数和参数的区别

参数：简单来说，模型参数就是模型内部的配置变量，可以用数据估计它的值。

具体来讲，模型参数有以下特征：

（1）进行模型预测时需要模型参数
（2）模型参数值可以定义模型功能
（3）模型参数用数据估计或数据学习得到
（4）模型参数一般不由实践者手动设置
（5）模型参数通常作为学习模型的一部分保存

通常使用优化算法估计模型参数，优化算法是对参数的可能值进行的一种有效搜索。

模型参数的一些例子包括：

（1）人工神经网络中的权重
（2）支持向量机中的支持向量
（3）线性回归或逻辑回归中的系数

超参数：：模型超参数是模型外部的配置，其值不能从数据估计得到。

具体特征有：

（1）模型超参数常应用于估计模型参数的过程中
（2）模型超参数通常由实践者直接指定
（3）模型超参数通常可以使用启发式方法来设置
（4）模型超参数通常根据给定的预测建模问题而调整

怎样得到它的最优值： 对于给定的问题，我们无法知道模型超参数的最优值。但我们可以使用经验法则来探寻其最优值，或复制用于其他问题的值，也可以通过反复试验的方法。

模型超参数的一些例子包括：

（1）训练神经网络的学习速率
（2）支持向量机的C和sigma超参数
（2）k邻域中的k

二者的联系：
当针对特定问题调整机器学习算法时，例如在使用网格搜索或随机搜索时，你将调整模型或命令的超参数，以发现一个可以使模型预测最熟练的模型参数。许多模型中重要的参数无法直接从数据中估计得到。例如，在K近邻分类模型中…这种类型的模型参数被称为调整参数，因为没有可用的分析公式来为其计算一个合适的值。

两者的区别：
模型超参数通常被称为模型参数，这种叫法很容易让人产生误解。解决这个问题的一个很好的经验法则如下：如果你必须手动指定一个“模型参数”，那么它可能就是一个模型超参数。

总结：
总而言之，模型参数是从数据中自动估计的，而模型超参数是手动设置的，并用于估计模型参数的过程。

超参数调优的方法：——可阅读《百面机器学习》P43

• 网格搜索
• 随机搜索
• 贝叶斯优化的方法

6.准确率，精确度，召回率，ROC曲线，AUC值

在介绍这些概念之前，先来看一下混淆矩阵：

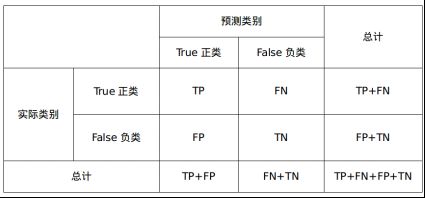
TP: True Positive,将正类预测类正类的样本数量（预测正确）
FN: False Negtive,将正类预测为负类的样本数量（type II error, 漏报）
FP: False Positive,将负类预测为正类的样本数量（type I error）
TN: True Negtive,将负类预测为负类的样本数量（预测正确）

准确度：准确度表示分类正确的样本数所占比例

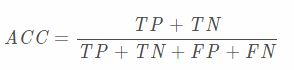
精确度、精度：该概念是针对“预测结果”而言的。表示预测为正类的样本中有多少是真的正样本

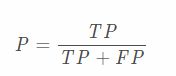
召回率：该概念是针对“原始样本”而言的。表示样本中的正例有多少被分类正确了

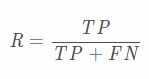
ROC曲线：在介绍ROC曲线之前，还需要引入其他概念：

1.敏感性Sensitivity、召回率Recall、hit rate、TPR（True Positive Rate）：表示样本中正类被分类正确的比例

$$TPR=TPTP+FNTPR=\frac{TP}{TP+FN}TPR=TP+FNTP$$
2.假阴性率FNR（False Negative Rate）:

$$FNR=FNTP+FN=1-TPRFNR=\frac{FN}{TP+FN}=1-TPRFNR=TP+FNFN=1-TPR$$
3.假阳性率FPR（False Positive Rate）：

$$FPR=FPFP+TN=1-TNRFPR=\frac{FP}{FP+TN}=1-TNRFPR=FP+TNFP=1-TNR$$
4.特异性specificity、真阴性率TNR（True Negative Rate）：表示样本中负类被分类正确的比例

$$TNR=TNFP+TNTNR=\frac{TN}{FP+TN}TNR=FP+TNTN$$

ROC（Receiver Operating Characteristic Curve）接受者特征曲线，是反应敏感性和特异性连续变量的综合指标。

ROC曲线图的横坐标是FPR，表示预测为正但实际为负的样本占所有负例样本的比例，纵坐标是TPR，，表示预测正类中实际负类就越多，纵坐标为TPR，表示预测为正且实际为正的样本占所有正例样本的比例，其值越大，表示预测正类中实际正类就越多。所以理想情况下，TPR应该越接近1越好，FPR越接近0越好。

经过上面的描述我们知道，ROC曲线的横坐标和纵坐标其实是没有相关性的，所以不能把ROC曲线当做一个函数曲线来分析，应该把ROC曲线看成无数个点，每个点都代表一个分类器，其横纵坐标表征了这个分类器的性能。为了更好的理解ROC曲线，我们先引入ROC空间，如下图所示。

AUC值：表示ROC曲线下的面积，即ROC曲线与x轴、（1，0）-（1，1）围绕的面积

参考：准确度、精确度、召回率、ROC曲线、AUC值

7.模型评估的方法

• Holdout检验
  它指的是将原始样本集合随机划分成训练集和验证集两部分，比如70%的训练集，30%验证集用于模型验证，包括绘制ROC曲线、计算精确率和召回率等指标来评估模型性能。
  缺点：验证集上计算出来的最后评估指标与原始分组有很大的关系，所以采用交叉检验的思想。
• 交叉检验
  K-fold验证：首先将全部样本划分成k个大小相等的样本子集；依次遍历这k个子集，每次把当前子集作为验证集，其余子集作为训练集，进行模型的训练和评估；最后把k次评估指标的平均值作为最终的评估指标。实际经验中，k经常取10.
  留一验证：每次留下1个样本作为测试集，其余所有样本为测试集。样本总数为n，依次对n个样本进行遍历，进行n次验证，再将评估指标求平均值得到最终的评估指标。
• 自助法
  自助法是基于自助采样的检验方法。对于总数为n的样本集合，进行n次的有放回的抽样，得到大小为n的训练集。n次采样的过程中，有的样本会被重复采样，有的样本没有被抽出过，将这些没有被抽出的样本的作为验证集，进行模型验证，这就是自助法的验证过程。（大约36.8%样本没有被抽到，和bagging有点类似）

参考：
《百面机器学习》

—————————————————————————————————————————————————
博主码字不易，大家关注点个赞转发再走呗 ，您的三连是激发我创作的源动力^ - ^