ICML 2022 | Meta提出鲁棒的多目标贝叶斯优化方法，有效应对输入噪声

©作者 | 杨泽群

单位 | 中国人民大学

研究方向 | 多模态学习

论文标题：

Robust Multi-Objective Bayesian Optimization Under Input Noise

论文链接：

https://arxiv.org/abs/2202.07549

项目链接：

https://github.com/facebookresearch/robust_mobo

本文是 facebook 发表于 ICML 2022 的一篇工作，其在理论角度上对有输入噪声的多目标贝叶斯优化进行了分析。

引言

本文面向多目标优化的输入噪声问题，结合贝叶斯优化和帕累托最优的思想设计并优化了全局多目标风险价值，以解决对输入噪声敏感的黑盒约束的问题。贝叶斯优化通过调整设计参数，可以优化高评估成本的黑盒性能指标。虽然现有很多方法被提出用于在输入噪声下优化单一目标，但目前仍然缺少能够解决存在多个目标对输入扰动敏感的实际问题的方法。

在这项工作中，作者提出了第一个鲁棒的多目标贝叶斯优化方法以应对输入噪声。作者将目标形式化为优化一种不确定目标的风险度量，即多变量风险值（MVaR）。由于直接优化 MVaR 在许多情况下在计算上是不可行的，作者提出了一种可扩展的、基于理论的方法来使用随机尺度来优化 MVaR。实验上而言，该方法在数据集上显著优于其他方法，并有效地实现了最优鲁棒设计。

▲ 图1：简易数据集上表明非鲁棒设计的多目标优化的最优值对输入噪声敏感，并给出了最优点集的选取演示。

这里通过图 1 来梳理一下作者提出的问题：左图中，非鲁棒设计（紫色 ）和鲁棒设计（绿色 ）的标称值使用正方形表示。加号标记表示每个设计在零均值高斯输入噪声下的目标值，标准差为 0.1。可以看到，虽然非鲁棒设计可能会获得局部较优的结果，但是其在输入扰动下的不稳定，容易导致更坏的表现；而鲁棒设计 的结果对于输入的扰动较小，对于输入噪声不敏感。 

中间的图中是对非鲁棒和鲁棒设计的 MVaR 集的说明，其中三角形表示在输入噪声分布下，每个设计的 MVaR 集的离散近似。在没有考虑噪声的情况下，紫色 正方形可以对应更好的值；但是在加以扰动后其风险（MVaR）较大，难以做到对于输入噪声的鲁棒。所以可以采用多变量风险值来刻画解的稳定性。右图是对不同风险集合的选择策略的描述，假设方法给出了在三个目标上的 MVaR 集合，风险的最优集是不同目标 MVaR 集的并集上的最优点集。

背景

多目标优化在多个黑盒函数之间进行权衡，其目标是识别最优权衡的帕累托边界和相应的最优设计的帕累托集 。考虑最大化黑盒函数： 其中 ， 是目标个数， 是紧搜索空间。又上述定义可以引出帕累托支配和帕累托边界的定义。若向量 帕累托支配于 ，记作 ，当且仅当 并且 满足 。

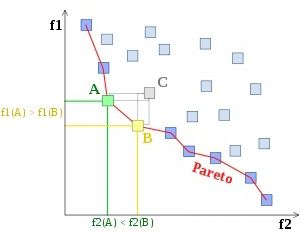
帕累托最优（Pareto optimality）是一种不能再改进的状态，不可能再改善某些个体或偏好准则而不使任何其他个体或准则受损。如果一种状态存在帕累托最优的改进，那么它被称作受帕累托支配的。一种状态如果是不受帕累托支配的，那么它被称作帕累托最优的或帕累托有效的，在优化问题中可以看作是最优点。这样的最优点组成的集合被称为帕累托边界。从下图中可以看出，A 和 B 是帕累托边界上的点，其都是对于 C 的支配。

▲ 图2：这里给出帕累托边界的一个例子。集合中的点表示可行的选择，这里认为更小的值是更优的，红线代表帕累托边界，其上面的样本点均是帕累托有效的。点 C 同时被点 A 和点 B 支配，所以其不在帕累托边界上。点 A 和点 B 不受任何其他点严格控制，因此位于边界上。

这里定义 的帕累托边界：

若 PARETO 中的元素满足黑盒的附加约束，则将相应的最优设计集认为是帕累托边界。而后，作者通过定义测度（超体积和超体积增量）来衡量不同帕累托边界的质量，即帕累托边界内部所包含区域的测度值。

方法

在这里首先要对于风险进行定义。由于期望风险测量可能并不总是与真正鲁棒性目标相一致，所以在这里采用概率风险进行分析，并得到以下定义：

上面给出了风险价值的定义，其得到了在噪声中 的一个下界 ，使得 有至少 的概率落在大于 的域内，并称之为概率风险，以此对单目标的噪声进行衡量。

而对于 Multivariate Value-at-Risk（MVaR）而言，所有的 个目标都是在相同的带噪样本中下进行评估的。作者在多目标的边界进行设计其是不同目标的帕累托边界，可以写成下面的形式：

由此，其定义了跨越设计空间的全局风险，是采用一系列点（见图 1 的三角形），在多目标情境下对于帕累托边界的进行鲁棒近似，这也是这篇文章的重要贡献之一。

▲ 图3：对于图1中toy数据的MVaR的构建过程

本文提出了 MARS 方法，通过引入切比雪夫尺度化展示了 VaR 和 MVaR 间的关系，并可以对 MVaR 集合进行估计。这里图 3 是对图 1 简易数据的 MVaR 集合构建的过程，其中左图中黑点表示对于标准差为 0.1，均值为 0 的高斯输入扰动的函数值，其背景是一个显示跨越目标空间的切比雪夫尺度化值的轮廓。中间的图给出了切比雪夫尺度化的概率密度和 的切比雪夫尺度化的风险值 ，黑线右侧的概率质量等于 。右图展示了通过文中所证明的定理构建出的关系，将 VaR 映射到 MVaR 中，绿色三角形代表了来自输入噪声分布的 MVaR 集的离散近似。

主要结果

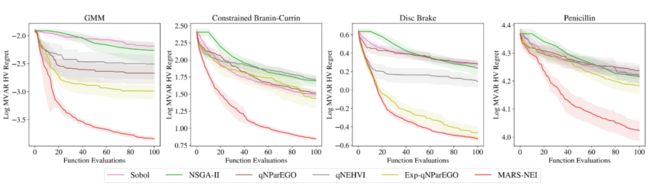
▲ 图4：在4个不同噪声数据集上的评估

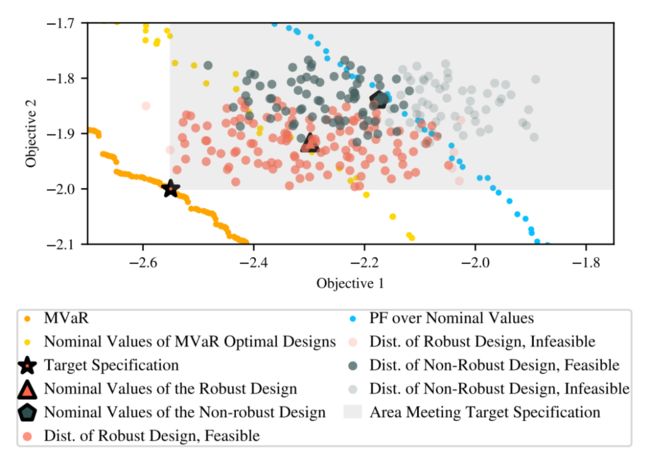
▲ 图5：虽然非鲁棒设计在无噪声目标（Nominal Values）下是可行的，但它位于设计空间中可行区域的边界附近，在输入扰动的情况下会违反黑盒中的约束，使得得到的解不可行

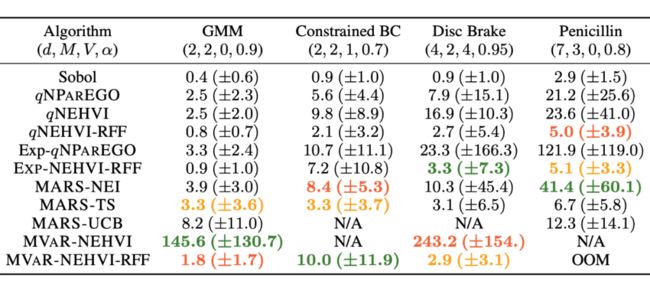
▲ 表1：不同算法的贝叶斯优化每次迭代的运行时间

图 4 展示了随训练进程的变化，各个算法的性能表现，这里采用全局 MVaR 和设计 MVaR 的差距的 HV 的对数值作为评价指标，可以说明设计的 MVaR 能否接近全局情况。在输入噪声的干预下，非鲁棒方法显著弱于鲁棒方法，而作者的方法由于其他对比方法。图 5 展示了在真实数据集中，选择鲁棒设计和非鲁棒设计分别的收益。这里可以看出通过 MVaR 学到的设计更接近于目标值，而非鲁棒设计得到的解更可能落入非可行域中。表 1 则展示了 MARS-based 方法在运行时间上的优势。

总结与思考

在这篇工作中，作者结合了贝叶斯优化和多目标融合的性质，从分布层面来对于输入噪声进行了分析，其通过设计 MVaR 风险并寻找多目标风险的帕累托最优，很好的结合了两个方法的特点，思路较为简单合理。对于其他的多源目标的优化，比如多模态、多视角、多任务学习而言，该方法指导我们可以从数据扰动风险的角度入手，来分析方法中潜在的输入噪声问题。

同时，由于方法简单但难以直观表述，作者用了较少篇幅就实现了对方法的清晰阐述，而后通过大量的铺垫清晰阐述文章的背景和主要贡献，并在附录中给出了大量的证明说明了其中引理的正确性。同时，作者仅通过两幅图像即说明主要的问题和方法，清晰的展示出了多目标情境下的鲁棒性问题。

而在方法层面，该方法采用一系列点对于分布边界进行了估计，其与基于 anchor 的方法，通过锚点选取来估计数据分布的思想较为类似，二者分别描述了分布边界和集散情况。后续可以对于噪声（输入噪声、标签噪声）情况下二者的关系进行深入思考。

更多阅读

#投 稿 通 道#

 让你的文字被更多人看到 

如何才能让更多的优质内容以更短路径到达读者群体，缩短读者寻找优质内容的成本呢？答案就是：你不认识的人。

总有一些你不认识的人，知道你想知道的东西。PaperWeekly 或许可以成为一座桥梁，促使不同背景、不同方向的学者和学术灵感相互碰撞，迸发出更多的可能性。 

PaperWeekly 鼓励高校实验室或个人，在我们的平台上分享各类优质内容，可以是最新论文解读，也可以是学术热点剖析、科研心得或竞赛经验讲解等。我们的目的只有一个，让知识真正流动起来。

 稿件基本要求：

• 文章确系个人原创作品，未曾在公开渠道发表，如为其他平台已发表或待发表的文章，请明确标注 

• 稿件建议以 markdown 格式撰写，文中配图以附件形式发送，要求图片清晰，无版权问题

• PaperWeekly 尊重原作者署名权，并将为每篇被采纳的原创首发稿件，提供业内具有竞争力稿酬，具体依据文章阅读量和文章质量阶梯制结算

 投稿通道：

• 投稿邮箱：[email protected] 

• 来稿请备注即时联系方式（微信），以便我们在稿件选用的第一时间联系作者

• 您也可以直接添加小编微信（pwbot02）快速投稿，备注：姓名-投稿

△长按添加PaperWeekly小编

现在，在「知乎」也能找到我们了

进入知乎首页搜索「PaperWeekly」

点击「关注」订阅我们的专栏吧

·