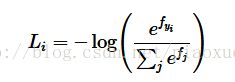斯坦福大学深度学习公开课cs231n学习笔记（9）softmax分类和神经网络分类代码实现

在前面的几节课中，讲述了神经网络的基本原理和参数的优化方法等，在这节课中，讲师前面的知识进行总结运用，通过构建Softmax分类器和一个小型的神经网络让我们有更加深入和直接的了解。我按照课中的步骤进行实现。

第一步：生成数据

N = 100 # number of points per class
D = 2 # dimensionality
K = 3 # number of classes
import numpy as np
import matplotlib.pyplot as plt
X = np.zeros((N*K,D)) # data matrix (each row = single example)
y = np.zeros(N*K, dtype='uint8') # class labels
for j in range(K):
  ix = range(N*j,N*(j+1))
#  print("ix:",ix)
  r = np.linspace(0.0,1,N) # radius
  t = np.linspace(j*4,(j+1)*4,N) + np.random.randn(N)*0.2 # theta
  X[ix] = np.c_[r*np.sin(t), r*np.cos(t)] #np.c_转换为多列数据
#  print("X[ix]:",X[ix])
  y[ix] = j #给300个点分类，每一百为一类，即[0，99]为0类，[100，199]为1类，[200,299]为2类
# lets visualize the data:
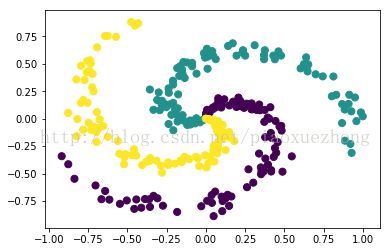
plt.scatter(X[:, 0], X[:, 1], c=y, s=50)#scatter画散点图；
#plt.scatter(X[:, 0], X[:, 1], c=y, s=40, cmap=plt.cm.Spectral)
plt.show()

程序解释：

程序中，X是大小为（300,2）矩阵数据，第一列数据为r*sin(t)，第二列数据为r*cos(t);其中，r是[0:0.01:1]的100个半径序列，t为和r相同大小的角度序列。

plt.scatter功能为显示散列数据。

第二步：训练softmax分类器

2.1初始化参数W和b

# initialize parameters randomly
W = 0.01 * np.random.randn(D,K)
b = np.zeros((1,K))

设置W为（2,3）权重矩阵，b为（1,3）偏置矩阵。

2.2求不同分类的分值

# compute class scores for a linear classifier
scores = np.dot(X, W) + b

在这个例子中有300个二维点数据，np.dot乘积运算，数组的分数将有大小[ 300×3 ]，即给出3个分类对应的分数。

2.3计算损失函数

由之前的课中我们知道softmax的损失函数计算公式为：

其中，log 内部式子的范围是[0,1]，当分类错误时，此值接近0，Li 将是正无穷；当分类正确时，此值接近1，Li 将接近0。

上述过程的实现为：

num_examples = X.shape[0]
# get unnormalized probabilities
exp_scores = np.exp(scores)
# normalize them for each example
probs = exp_scores / np.sum(exp_scores, axis=1, keepdims=True) #每个点分类的得分所占概率（包括正确分类和错误分类）,300*3
corect_logprobs = -np.log(probs[range(num_examples),y]) #probs[range(num_examples),y]是正确分类的概率

probs为[300,3]矩阵，元素对应不同分类的概率值。corect_logprobs对应Li 值，程序中y为数据生成时的标记，值为[100*0,100*1,100*2]，即对应分类类别0,1,2。
整个softmax分类器的损失被定义为包含训练实例和正则化两部分的平均交叉熵损失：

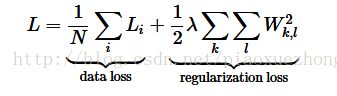
上面公式的实现为：

# compute the loss: average cross-entropy loss and regularization
data_loss = np.sum(corect_logprobs)/num_examples
reg_loss = 0.5*reg*np.sum(W*W)
loss = data_loss + reg_loss

其中，公式中的λ存放在reg中。

2.4反向传播计算梯度

有了上面计算损失函数的方法，现在需要使用梯度下降减小损失函数值，即从随机参数开始，评估损失函数相对于参数的梯度，以便知道如何改变参数以减少损失。引入中间变量p，它是（正规化）概率的一个向量：

在softmax学习笔记中，我们知道对Li求导结果为：

假设计算出一组概率： p=[0.2,0.3,0.5]; 而正确的分类是中间那一类，所以用上面的求导公式可以求得：df = [0.2, -0.7, 0.5]；

上述公式实现为：

dscores = probs
dscores[range(num_examples),y] -= 1
dscores /= num_examples

计算分值公式为： scores = np.dot(X, W) + b，现在求出了 dscores，通过对两边分别求导，可以反推出： dW 和 db

dW = np.dot(X.T, dscores)
db = np.sum(dscores, axis=0, keepdims=True)
dW += reg*W # don't forget the regularization gradient

其中，对W求导时，两边同乘 X.T。第三行dW加上了正则项（1/2*λ*W^2）部分对W的导数（λW），

2.5 参数更新

W += -step_size * dW
b += -step_size * db

综上，我们便完成了整个softmax分类函数的训练过程，整个过程实现代码如下：

N = 100 # number of points per class
D = 2 # dimensionality
K = 3 # number of classes
import numpy as np
import matplotlib.pyplot as plt
X = np.zeros((N*K,D)) # data matrix (each row = single example)
y = np.zeros(N*K, dtype='uint8') # class labels
for j in range(K):
  ix = range(N*j,N*(j+1))
#  print("ix:",ix)
  r = np.linspace(0.0,1,N) # radius
  t = np.linspace(j*4,(j+1)*4,N) + np.random.randn(N)*0.2 # theta
  X[ix] = np.c_[r*np.sin(t), r*np.cos(t)] #np.c_转换为多列数据
#  print("X[ix]:",X[ix])
  y[ix] = j
# lets visualize the data:
plt.scatter(X[:, 0], X[:, 1], c=y, s=50)
#plt.scatter(X[:, 0], X[:, 1], c=y, s=40, cmap=plt.cm.Spectral)
plt.show()

#Train a Linear Classifier

# initialize parameters randomly
W = 0.01 * np.random.randn(D,K)
b = np.zeros((1,K))

# some hyperparameters
step_size = 1e-0
reg = 1e-3 # regularization strength

# gradient descent loop
num_examples = X.shape[0]
for i in range(200):
  
  # evaluate class scores, [N x K]
  scores = np.dot(X, W) + b 
  
  # compute the class probabilities
  exp_scores = np.exp(scores)
  tmp= np.sum(exp_scores, axis=1, keepdims=True) 
  probs = exp_scores / np.sum(exp_scores, axis=1, keepdims=True) # [N x K]
  
  # compute the loss: average cross-entropy loss and regularization
  corect_logprobs = -np.log(probs[range(num_examples),y])
  data_loss = np.sum(corect_logprobs)/num_examples
  reg_loss = 0.5*reg*np.sum(W*W)
  loss = data_loss + reg_loss
  if i % 10 == 0:
    print ("iteration %d: loss %f" % (i, loss))
  
  # compute the gradient on scores
  dscores = probs
  dscores[range(num_examples),y] -= 1
  dscores /= num_examples
  
  # backpropate the gradient to the parameters (W,b)
  dW = np.dot(X.T, dscores)
  db = np.sum(dscores, axis=0, keepdims=True)
  
  dW += reg*W # regularization gradient
  
  # perform a parameter update
  W += -step_size * dW
  b += -step_size * db

经过若干次迭代后（函数中设置最大迭代次数为200），得到参数W和b。之后我们可以看下训练后的神经网络的准确性，即看一下我们假设第二类是正确分类所占的比重是多少。

# evaluate training set accuracy
scores = np.dot(X, W) + b
predicted_class = np.argmax(scores, axis=1)
print ('training accuracy: %.2f' % (np.mean(predicted_class == y)))

上述过程的运行结果为：

iteration 0: loss 1.098034
iteration 10: loss 0.905211
iteration 20: loss 0.833959
iteration 30: loss 0.801773
iteration 40: loss 0.785123
iteration 50: loss 0.775711
iteration 60: loss 0.770056
iteration 70: loss 0.766508
iteration 80: loss 0.764208
iteration 90: loss 0.762681
iteration 100: loss 0.761647
iteration 110: loss 0.760935
iteration 120: loss 0.760440
iteration 130: loss 0.760092
iteration 140: loss 0.759845
iteration 150: loss 0.759669
iteration 160: loss 0.759543
iteration 170: loss 0.759451
iteration 180: loss 0.759385
iteration 190: loss 0.759337
training accuracy: 0.53

程序得到的分类准确性为53%，由于生成的数据本身不是线性的，所以使用线性分类器得到这个结果也是情理之中的事，使用下面的代码可以将分类边界绘制出来：

# plot the resulting classifier
h = 0.02
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
                     np.arange(y_min, y_max, h))
Z = np.dot(np.c_[xx.ravel(), yy.ravel()], W) + b
Z = np.argmax(Z, axis=1)
Z = Z.reshape(xx.shape)
fig = plt.figure()
plt.contourf(xx, yy, Z, cmap=plt.cm.Spectral, alpha=0.8)
plt.scatter(X[:, 0], X[:, 1], c=y, s=40)
plt.xlim(xx.min(), xx.max())
plt.ylim(yy.min(), yy.max())
plt.show()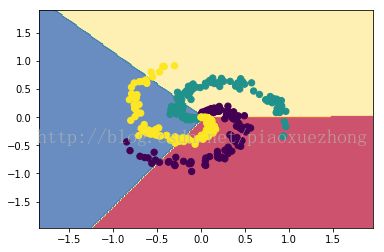

训练神经网络：

上面用线性分类器分类的结果为53%，可见效果一般，所以下面使用神经网络进行测试，对比下线性分类器的效果如何？

#generate data
N = 100 # number of points per class
D = 2 # dimensionality
K = 3 # number of classes
import numpy as np
import matplotlib.pyplot as plt
X = np.zeros((N*K,D)) # data matrix (each row = single example)
y = np.zeros(N*K, dtype='uint8') # class labels
for j in range(K):
  ix = range(N*j,N*(j+1))
#  print("ix:",ix)
  r = np.linspace(0.0,1,N) # radius
  t = np.linspace(j*4,(j+1)*4,N) + np.random.randn(N)*0.2 # theta
  X[ix] = np.c_[r*np.sin(t), r*np.cos(t)]
#  print("X[ix]:",X[ix])
  y[ix] = j
# lets visualize the data:
plt.scatter(X[:, 0], X[:, 1], c=y, s=50)
#plt.scatter(X[:, 0], X[:, 1], c=y, s=40, cmap=plt.cm.Spectral)
plt.show()

# initialize parameters randomly
h = 100 # size of hidden layer
W = 0.01 * np.random.randn(D,h)
b = np.zeros((1,h))
W2 = 0.01 * np.random.randn(h,K)
b2 = np.zeros((1,K))

# some hyperparameters
step_size = 1e-0
reg = 1e-3 # regularization strength

# gradient descent loop
num_examples = X.shape[0]
for i in range(10000):
  
  # evaluate class scores, [N x K]
  hidden_layer = np.maximum(0, np.dot(X, W) + b) # note, ReLU activation
  scores = np.dot(hidden_layer, W2) + b2
  
  # compute the class probabilities
  exp_scores = np.exp(scores)
  probs = exp_scores / np.sum(exp_scores, axis=1, keepdims=True) # [N x K]
  
  # compute the loss: average cross-entropy loss and regularization
  corect_logprobs = -np.log(probs[range(num_examples),y])
  data_loss = np.sum(corect_logprobs)/num_examples
  reg_loss = 0.5*reg*np.sum(W*W) + 0.5*reg*np.sum(W2*W2)
  loss = data_loss + reg_loss
  if i % 1000 == 0:
    print ("iteration %d: loss %f" % (i, loss))
  
  # compute the gradient on scores
  dscores = probs
  dscores[range(num_examples),y] -= 1
  dscores /= num_examples
  
  # backpropate the gradient to the parameters
  # first backprop into parameters W2 and b2
  dW2 = np.dot(hidden_layer.T, dscores)
  db2 = np.sum(dscores, axis=0, keepdims=True)
  # next backprop into hidden layer
  dhidden = np.dot(dscores, W2.T)
  # backprop the ReLU non-linearity
  dhidden[hidden_layer <= 0] = 0
  # finally into W,b
  dW = np.dot(X.T, dhidden)
  db = np.sum(dhidden, axis=0, keepdims=True)
  
  # add regularization gradient contribution
  dW2 += reg * W2
  dW += reg * W
  
  # perform a parameter update
  W += -step_size * dW
  b += -step_size * db
  W2 += -step_size * dW2
  b2 += -step_size * db2
  
# evaluate training set accuracy
hidden_layer = np.maximum(0, np.dot(X, W) + b)
scores = np.dot(hidden_layer, W2) + b2
predicted_class = np.argmax(scores, axis=1)
print ('training accuracy: %.2f' % (np.mean(predicted_class == y)))

# plot the resulting classifier
h = 0.02
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
                     np.arange(y_min, y_max, h))
Z = np.dot(np.maximum(0, np.dot(np.c_[xx.ravel(), yy.ravel()], W) + b), W2) + b2
Z = np.argmax(Z, axis=1)
Z = Z.reshape(xx.shape)
fig = plt.figure()
plt.contourf(xx, yy, Z, cmap=plt.cm.Spectral, alpha=0.8)
plt.scatter(X[:, 0], X[:, 1], c=y, s=40)
plt.xlim(xx.min(), xx.max())
plt.ylim(yy.min(), yy.max())
plt.show()

程序解释：

上面代码构建的是一个两层神经网络，第一层隐层有100个神经元，输出层有3种分类，激活函数使用的是ReLU非线性函数：

对r求导，得：

当求导梯度小于0时，将梯度值设为零，即程序中的语句：dhidden[hidden_layer <= 0] = 0

其他步骤类似于softmax分类器，此函数的运行结果为：

iteration 0: loss 1.098593
iteration 1000: loss 0.313864
iteration 2000: loss 0.261329
iteration 3000: loss 0.254359
iteration 4000: loss 0.250366
iteration 5000: loss 0.248206
iteration 6000: loss 0.247869
iteration 7000: loss 0.247758
iteration 8000: loss 0.247667
iteration 9000: loss 0.247605
training accuracy: 0.99

准确性为99%，比第一种softmax线性分类器准确性提高了很多，其决策边界图为：

参考：

http://cs231n.github.io/neural-networks-case-study/

http://www.yiibai.com/numpy/

http://matplotlib.org/index.html