Skip-gram & CBOW 的一些理解
Skip-gram & CBOW 的一些理解
文章目录
- Skip-gram & CBOW 的一些理解
-
- 〇、前言
- 一、背景
- 二、基础结构
-
- 2.1 One-hot投影成隐向量
- 2.2 利用一个词预测一个词
- 2.3 损失函数的计算
- 三、CBOW
- 四、Skip-gram
- 五、一些训练时用到的tricks
-
- 5.1 H i e r a r c h i c a l S o f t m a x Hierarchical\ Softmax Hierarchical Softmax
- 5.2 N e g a t i v e S a m p l i n g Negative\ Sampling Negative Sampling
- 六、文中的一些细节
-
- 6.1 对学习到的结构和语义上联系的实验
- 6.2 对短语的学习
- 6.3 学习到的向量的联系
- 6.4 一些结果的讨论
-
- 6.4.1 H i e r a r c h i c a l S o f t m a x Hierarchical\ Softmax Hierarchical Softmax和 N e g a t i v e S a m p l i n g Negative\ Sampling Negative Sampling的对比
- 6.4.2 CBOW和Skip-gram的对比
- 七、一些我的想法
-
- 7.1 关于多义词
- 7.2 关于社会计算
- 八、引用
〇、前言
如果要列举近些年来的机器学习的突破进展,Skip-gram的提出一定在近20年里能排到前20。在近两年的文章中,依然可以看到它的各种变种在各种领域的应用。因此就想去深入的了解一下这个算法,根据[4]的推荐,我读了三篇文章,它们分别是:
1. E f f i c i e n t E s t i m a t i o n o f W o r d R e p r e s e n t a t i o n s i n V e c t o r S p a c e , I C L R 2013 1.\ Efficient\ Estimation\ of\ Word\ Representations\ in\ Vector\ Space\ , ICLR \ 2013 1. Efficient Estimation of Word Representations in Vector Space ,ICLR 2013[1], 这一篇是提出Skip-gram的文章。
2. D i s t r i b u t e d R e p r e s e n t a t i o n s o f W o r d s a n d P h r a s e s a n d t h e i r C o m p o s i t i o n a l i t y , N I P S 2013 2.\ Distributed\ Representations\ of\ Words\ and\ Phrases\ and\ their\ Compositionality,\ NIPS\ 2013 2. Distributed Representations of Words and Phrases and their Compositionality, NIPS 2013[2], 这一篇是Skip-gram作者为了解释原文中没有详细解释的一些tricks。
3. w o r d 2 v e c P a r a m e t e r L e a r n i n g E x p l a i n e d , D B L P 2016 3.\ word2vec\ Parameter\ Learning\ Explained\ ,DBLP\ 2016 3. word2vec Parameter Learning Explained ,DBLP 2016[3], 这篇文章是另外一个人较为详细的解释了Skip-gram和CBOW中的一些细节,对于理解Skip-gram 和 CBOW我觉得非常有用。
后面的段落会简单写一些我对这三篇文章的理解,而非简单的翻译。
本文在完成前仅参考了[4]进行相关文章的调研,没有读其他的中文博客,对同一个单词,可能会有一些表达上的差异,敬请谅解。
一、背景
我感觉自然语言处理领域,非常重要的一个内容就是学习到基础单元的表征,而且这种表征往往需要融合进上下文的信息。比如在做文本翻译时,学习到一个单词或者短语的表征对于文本翻译非常重要,而往往要通过一个词在一段话中的位置来进行学习;在做商品推荐时,学习到一个商品或者一筐商品的表征也非常重要,而往往需要通过一个购买者的多次购买行为进行学习;甚至在图上,由于Random Walk出的序列在一定意义上也具有语义上的信息,可以拿Random Walk出的结果进行学习,得到每个点的表征。
但是传统的机器学习做法主要有以下的问题:
- 计算开销过大,训练一次花费时间和资源过多,导致训练难度极大
- 很难同时学到 语言的结构 syntactic和 语义semantic上的关系。如[1]中提到RNN能很好的学习到结构上的关系,但是较难学习到语义上的关系。
因此呢,在我看来,为了解决这两个问题,作者提出了CBOW和Skip-gram两个模型。
二、基础结构
简单来说CBOW是以多预测一,Skip-gram是以一预测多,为了便于理解,结合了[3]文章的一些思路,我觉得可以通过先构建一个简化的CBOW和与Skip-gram即一个一预测一的模型,从而理解CBOW和Skip-gram的原始思路。

图 一 一 个 简 单 的 一 预 测 一 模 型 图一\ 一个简单的一预测一模型 图一 一个简单的一预测一模型
其实可以把这个一预测一模型再拆成了两个,一个是将one hot编码投影成一个隐向量,另外一个是通过隐向量来进行预测,我也会分为两个部分进行解释。
2.1 One-hot投影成隐向量
图 二 o n e − h o t 编 码 投 影 成 隐 向 量 图二\ one-hot编码投影成隐向量 图二 one−hot编码投影成隐向量
首先,对每个词肯定只能将它进行one-hot编码,即如果总共有 V V V个词,则将每个词编码成一个长度为 V V V的向量,其中第 i i i个位为1,其他位为0。
既然这样,为了学到每个单词的表征,可以将它通过一个全连接层,即乘上一个 V × N V \times N V×N的矩阵,这样本来每一个单词是 1 × V 1\times V 1×V的one-hot编码,现在变成了了一个 1 × N 1\times N 1×N的向量。
这样看起来对于每一个词得到它的向量复杂度 O ( V N ) O(VN) O(VN)的,其实假设要第 k k k个向量的表征,由于它只有第 k k k位为1,它乘一个 V × N V \times N V×N 的矩阵,这样得到的结果其实刚好是这个矩阵的第 k k k行,因此可以 O ( N ) O(N) O(N)得到它的表征,记作 v k v_k vk。
指的一提的是 N N N一般可选50到600。
2.2 利用一个词预测一个词
图 三 利 用 一 个 词 来 预 测 另 外 一 个 词 图三\ 利用一个词来预测另外一个词 图三 利用一个词来预测另外一个词
由于这里的任务是通过一个词预测一个词(虽然看起来比较没有道理),我们首先需要要得到已知这个词的表征,通过2.1的结构,可以得到这个词的表征 v k v_k vk,也记作 h \textbf h h它是一个 1 × N 1\times N 1×N的向量 。
得到这个词的表征之后,可以将它通过一个全连接层,即乘上一个 N × V N\times V N×V的矩阵 W ′ W' W′,可以得到一个 1 × V 1\times V 1×V 的向量 u \textbf u u,我们将它第 i i i维的意义定义为预测结果是第 i i i个词的置信,即设 W ′ W' W′的第 i i i列为 v i ′ \textbf v'_i vi′,则有 v i ′ h = u i \textbf v'_i\textbf h = u_i vi′h=ui,接着用一个 s o f t m a x softmax softmax进行归一化即可得到第k个词预测出每个词的概率,即
P ( 第 j 个 词 ∣ 第 k 个 词 ) = y j = exp ( u j ) ∑ j ′ = 1 V exp ( u j ′ ) P(第j个词|第k个词) = y_j = \frac{\exp(u_j)}{\sum_{j'=1}^V\exp(u_{j'})} P(第j个词∣第k个词)=yj=∑j′=1Vexp(uj′)exp(uj)
2.3 损失函数的计算
由于我们的目标显然是要最大化 P ( 第 k 个 词 应 该 预 测 出 的 词 ∣ 第 k 个 词 ) P(第k个词应该预测出的词|第k个词) P(第k个词应该预测出的词∣第k个词),由于 log \log log函数是单调的,即可最大化 log ( P ( 第 k 个 词 应 该 预 测 出 的 词 ∣ 第 k 个 词 ) ) \log(P(第k个词应该预测出的词|第k个词)) log(P(第k个词应该预测出的词∣第k个词)),假设第 k k k个词应该预测出的词是第 o o o个词,即有
log ( P ( 第 o 个 词 ∣ 第 k 个 词 ) ) = log ( exp ( u o ) ∑ j ′ = 1 V exp ( u j ′ ) ) = u o − log ∑ j ′ = 1 V exp ( u j ′ ) = − E \log(P(第o个词|第k个词)) = \log(\frac{\exp(u_o)}{\sum_{j'=1}^V\exp(u_{j'})})=\\ u_o - \log\sum_{j'=1}^V\exp(u_{j'}) = -E log(P(第o个词∣第k个词))=log(∑j′=1Vexp(uj′)exp(uo))=uo−logj′=1∑Vexp(uj′)=−E
即目标是最小化 E = − u o + log ∑ j ′ = 1 V exp ( u j ′ ) E= -u_o + \log\sum_{j'=1}^V\exp(u_{j'}) E=−uo+log∑j′=1Vexp(uj′)
由于过程中所有式子都是可导的,因此显然是可以反向传播的,就可以train起来了。
三、CBOW
图 四 C B O W 的 结 构 图四\ CBOW的结构 图四 CBOW的结构
CBOW如上图所示,是通过综合第 t t t个时间的上下文信息,来预测第 t t t个时间的单词的一种模型,目前依照我的理解,应该没必要有下文,只要是多预测一即可,但是原文写得确实是进行对称的时间区间的预测,因此我觉得这样结果可能会好一些。
对于本文第二部分的基础结构来说,
- CBOW对2.1这一部分没有变化;
- CBOW对2.2这一部分改为了利用多个词来预测一个词,思路也很简单,假设用 C C C个词分别为 j 1 , j 2 , ⋯ , j C j_1,j_2,\cdots ,j_C j1,j2,⋯,jC进行预测,先分别和2.2类似,求得他们的表征 v j 1 , v j 2 , ⋯ , v j C v_{j_1},v_{j_2},\cdots ,v_{j_C} vj1,vj2,⋯,vjC则求一个向量 h = ∑ i = 1 C v j i C \textbf{h} = \frac{\sum_{i=1}^Cv_{j_i}}{C} h=C∑i=1Cvji,接着输入到和2.2相同的输出的全连接层中得到预测结果即可;
- CBOW对2.3的这一部分损失函数不变,但是由于变成了多预测一,往回反向传播的式子有一些变化,但不是重点,在此就不赘述了。
四、Skip-gram
图 五 S k i p − g r a m 的 结 构 图五\ Skip-gram的结构 图五 Skip−gram的结构
Skip-gram如上图所示,是通过综合第 t t t个时间信息,来预测第 t t t个时间的上下文的一种模型,目前依照我的理解,应该没必要有下文,只要是一预测多即可,但是原文写得确实是进行对称的时间区间的预测,因此我觉得这样结果可能会好一些。
这个其实看起来比较没有道理,知道一个词怎么就能知道它的上下文了呢,在此我讲一下我的理解。因为其实一个简单的全连接层不是特别能进行预测工作,我们用Skip-gram主要要做的其实是学习一个词的表征,核心任务不在于预测,这里这个预测只是将上下文的信息嵌入到这个词的表征中,仅此而已。
那对于本文第二部分的基础结构来说,
-
Skip-gram对2.1这一部分没有变化;
-
Skip-gram对2.2这一部分改为了利用一个词来预测多个词 j 1 , j 2 , ⋯ j n j_1,j_2,\cdots\,j_n j1,j2,⋯jn,思路也很简单,先和2.2相同,求得这个词的表征 v k v_{k} vk,接着输入到和2.2相同的输出的全连接层中得到了预测结果 u k u_k uk。要注意的是即使要预测的是 C C C个词,但是仍然只使用一个全连接层,而非使用 C C C个,用得到的一个结果 u k u_k uk去算损失函数。
-
Skip-gram对2.3的这一部分损失函数即改变为了
E = − log ( 第 j 1 个 词 , 第 j 2 个 词 , ⋯ , 第 j C 个 词 ∣ 第 k 个 词 ) = − log ( ∏ i = 1 C exp ( u j i ) ∑ j ′ = 1 V exp ( u j ′ ) ) = − ∑ j = 1 C u j i + C ∗ log ∑ j ′ = 1 V exp ( u j ′ ) E = -\log(第j_1个词,第j_2个词,\cdots,第j_C个词 | 第k个词) = \\ -\log(\prod_{i=1}^C\frac{\exp(u_{j_i})}{\sum_{j'=1}^V\exp(u_{j'})})=\\ -\sum _{j=1}^Cu_{j_i} + C*\log\sum_{j'=1}^V\exp(u_{j'}) E=−log(第j1个词,第j2个词,⋯,第jC个词∣第k个词)=−log(i=1∏C∑j′=1Vexp(uj′)exp(uji))=−j=1∑Cuji+C∗logj′=1∑Vexp(uj′)
五、一些训练时用到的tricks
注意到每次损失函数的计算复杂度都是 O ( V ) O(V) O(V)的,当语料库较大时,复杂度显然是不可接受的,因为跑一个句子里的一个词就要 O ( V ) O(V) O(V), V V V有可能是十万级,百万级的。作者为了解决这个问题,提出了两个办法,一个称为 H i e r a r c h i c a l S o f t m a x Hierarchical\ Softmax Hierarchical Softmax,另一个则是 N e g a t i v e S a m p l i n g ( 负 采 样 ) Negative\ Sampling(负采样) Negative Sampling(负采样)。
5.1 H i e r a r c h i c a l S o f t m a x Hierarchical\ Softmax Hierarchical Softmax
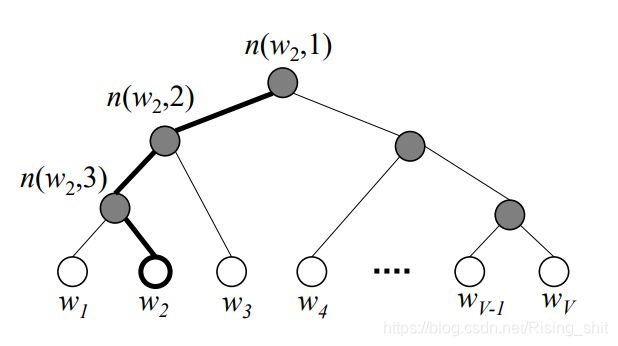
图 六 h i e r a r c h i c a l s o f t m a x 图六\ hierarchical\ softmax 图六 hierarchical softmax
由于无论是多预测一,还是一预测多,求得输入词的表征复杂度都较低,而计算输出为每个词的置信度复杂度为$O(V) , 复 杂 度 较 大 , 而 在 训 练 时 其 实 只 关 心 输 出 为 应 该 输 出 的 词 , 即 ,复杂度较大,而在训练时其实只关心输出为应该输出的词,即 ,复杂度较大,而在训练时其实只关心输出为应该输出的词,即词o$的置信度,因此可以设计一种结构较快的求出 词 o 词o 词o的置信度。
作者设计了一种基于 h u f f m a n huffman huffman树的做法,为什么用 h u f f m a n huffman huffman树其实也是为了降低复杂度,这样频繁被询问的词所需要查找到的次数较小,但是复杂度上限就是 log ( V ) \log(V) log(V),因此我觉得随便搞个二叉树也行,本身只是为了降低复杂度。
具体做法为
-
首先将 V V V个词作为了 h u f f m a n huffman huffman树的叶子节点,根据 h u f f m a n huffman huffman编码的方式进行合并。
-
其次定义了一个函数 n ( i , j ) n(i,j) n(i,j),表示从根节点到第 i i i个词,走出 j j j步到达的节点,如图六所示,定义 L ( i ) L(i) L(i)表示根节点到第 i i i个节点所需要走的步,即 n ( i , L ( i ) ) n(i,L(i)) n(i,L(i))就是第 i i i个词,定义 c h ( i ) ch(i) ch(i)表示第 i i i个节点的左儿子,定义 [ [ p ] ] [\![p]\!] [[p]]表示p为真的话,返回1,否则返回-1。
-
接着给除了叶子节点以外的 n − 1 n-1 n−1个节点各赋予了一个表征 v t i ′ \textbf v'_{t_i} vti′
-
最后有
p ( 第 o 个 词 ∣ 已 知 的 词 ) = ∏ j = 1 L ( o ) σ ( [ [ n ( o , j + 1 ) = c h ( n ( o , j ) ) ] ] ⋅ v n ( o , j ) ′ h ) p(第o个词|已知的词) = \prod_{j=1}^{L(o)}\sigma([\![n(o,j+1)=ch(n(o,j))]\!]\cdot \textbf v'_{n(o,j)}\textbf h) p(第o个词∣已知的词)=j=1∏L(o)σ([[n(o,j+1)=ch(n(o,j))]]⋅vn(o,j)′h)
其中 h \textbf h h为已知词的表征。这个式子大致的意思即为,从根往下找第 o o o个词,如果要走左儿子,则乘 σ ( v n ( o , j ) ′ h ) \sigma(\textbf v'_{n(o,j)}\textbf h) σ(vn(o,j)′h),否则乘 σ ( − v n ( o , j ) ′ h ) \sigma(-\textbf v'_{n(o,j)}\textbf h) σ(−vn(o,j)′h),有容斥的思想在其中。 -
损失函数的计算也是基于此的,就不赘述了。
5.2 N e g a t i v e S a m p l i n g Negative\ Sampling Negative Sampling
相对来说 N e g a t i v e S a m p l i n g Negative\ Sampling Negative Sampling(负采样)是一种更直观的方法,由于正样本往往只有很少的几个,负样本非常多,那就采样一些进行算,最后的损失函数为
log ( σ ( u o ) ) + ∑ 采 样 出 的 w j log ( σ ( − u w j ) ) \log(\sigma(u_o))+\sum_{采样出的w_j}\log(\sigma(-u_{w_j})) log(σ(uo))+采样出的wj∑log(σ(−uwj))
如何采一个好的样比较讲究,考虑到出现频率较高的单词往往没什么特别大意义,如 a , a n d , t h e a,and,the a,and,the这些,作者构造了一个分布 p ( 第 i 个 词 被 采 样 ) = 1 − t c n t ( 第 i 个 词 ) ) p(第i个词被采样) = 1-\sqrt{\frac{t}{cnt(第i个词)}}) p(第i个词被采样)=1−cnt(第i个词)t), t t t是手动选的一个置信度,通常为 1 0 − 5 10^{-5} 10−5,有趣的是 p 3 4 p^{\frac 3 4} p43才是最后作者用的分别,他认为 3 4 \frac 3 4 43 次方会比较好。
六、文中的一些细节
6.1 对学习到的结构和语义上联系的实验
作者做了一个有趣的实验,来证明它真的学习到了结构和语义上的联系。我觉得这个实验对于理解学习到的结果非常有意义,即通过向量的加减来证明学习到的联系。
举个例子,设 V ( i ) V(i) V(i)表示词 i i i学习到的向量,那么根据我们的理解 V ( C h i n a ) − V ( B e i j i n g ) + V ( T o k y o ) = ? V(China)-V(Beijing)+V(Tokyo)=? V(China)−V(Beijing)+V(Tokyo)=?,显然答案应该是 V ( J a p a n ) V(Japan) V(Japan)。作者通过找距离问号向量最近的向量,来看看是不是 V ( J a p a n ) V(Japan) V(Japan)来验证,发现居然真的是,来证明了它学习到的结果比较优秀。他选取了五组语义上的(如城市关系)以及九组结构上的(如动词和名词),来加以验证,结果如下图。

图 七 对 语 义 和 结 构 上 的 学 习 图七\ 对语义和结构上的学习 图七 对语义和结构上的学习
6.2 对短语的学习
其实我觉得更高级的任务是去学习短语,因为真实的行为和短语的关系甚至可能更大,比如购买商品都是以框为单位,而非以单个商品为单位,在这里呢,作者用了一个较为简单的方法来学习短语,即把短语当成一个词,进行学习。因为短语组合可能比较固定,所以语料库很容易覆盖所有的短语。那么如何判断短语呢,作者用了一种估价函数 s c o r e ( i , j ) = c n t ( i , j ) − δ c n t ( i ) ∗ c n t ( j ) score(i,j)=\frac{cnt(i,j)-\delta}{cnt(i)*cnt(j)} score(i,j)=cnt(i)∗cnt(j)cnt(i,j)−δ,即两个一起出现的次数除以两个各自出现的次数,如果超过一定比例,则认为是短语。这样迭代得构造即可。
6.3 学习到的向量的联系
图 八 学 到 短 语 的 联 系 图八\ 学到短语的联系 图八 学到短语的联系
有趣的加了学习短语之后,去找离它最近的单词和短语,使用Skip-gram,可以得到如图八的结果。这样看来用 h u f f m a n 树 huffman树 huffman树进行优化结果很好。第一个人是达伽马,航海家;第二个是贝加尔湖,和咸海比较类似;第三个是一个登月的人;第四个是一个海;第五个是象棋大师,对应卡斯帕罗夫也不错。
6.4 一些结果的讨论
6.4.1 H i e r a r c h i c a l S o f t m a x Hierarchical\ Softmax Hierarchical Softmax和 N e g a t i v e S a m p l i n g Negative\ Sampling Negative Sampling的对比
图 九 H i e r a r c h i c a l S o f t m a x 和 N e g a t i v e S a m p l i n g 的 对 比 图九\ Hierarchical\ Softmax和Negative\ Sampling的对比 图九 Hierarchical Softmax和Negative Sampling的对比
其实总得来说在实验数据上显示的是负采样更好一些
6.4.2 CBOW和Skip-gram的对比
图 十 C B O W 和 S k i p − g r a m 的 对 比 图十\ CBOW和Skip-gram的对比 图十 CBOW和Skip−gram的对比
在结构上的学习,Skip-gram相对比CBOW差了一些,但是在语义上的结果,Skip-gram有极大的提升。
七、一些我的想法
7.1 关于多义词
我感觉在自然语言处理上,应该会很经常的有多义词的出现。比如就人话里就会有很多多义词,比如苹果可能是一个品牌,也有可能是一个水果;再比如对于一个站点,它在某一层次来说,可能是一个交通枢纽,在某一层次也有可能只是一个普通站点;对于这个的学习,我觉得应该会有很多文章,可惜我还没读到,不过我猜可能可以用 a t t e n t i o n attention attention的做法去学习到,所以我打算下一篇先去读 a t t e n t i o n i s a l l y o u r n e e d attention\ is\ all\ your\ need attention is all your need。
7.2 关于社会计算
这部分仅在提交给社会计算大作业的版本中有。
由于大一下和大二做了一些关于图上的工作,主要是异质图的表示学习,又了解到社会计算和图的关系非常紧密,就选了社会计算课,希望再了解一些图上的知识,也确实收获了很多。
本课学到的诸如传播模型等,我觉得可以很好的利用在异质图的采样上,采样之后得到一个序列,这里就需要RNN或者本文提到的一些模型进行处理去得到图的表征。
总而言之,相信未来各自算法都是基于图的,图才更能模拟出现实的结构,因此我觉得学社会计算这个课非常有必要,也得到了很多比较前沿的知识,感觉体验非常好。
八、引用
[1] Mikolov T , Chen K , Corrado G , et al. Efficient Estimation of Word Representations in Vector Space[J]. Computer Science, 2013.
[2] Mikolov T , Sutskever I , Kai C , et al. Distributed Representations of Words and Phrases and their Compositionality[J]. Advances in neural information processing systems, 2013, 26.
[3] Rong X . word2vec Parameter Learning Explained[J]. Computer Science, 2014.
[4] https://zhuanlan.zhihu.com/p/39751353