Numpy基础教程
文章目录
- Numpy
- 简单例子
- 数组创建
- 打印数组
- 基本操作
- 通函数
- 索引、切片和迭代
- 形状操纵
-
- 改变数组的形状
- 将不同数组堆叠在一起
- 将一个数组拆分成几个较小的数组(分割)
-
- 纵向分割
- 横向分割
- 错误的分割
- 不等量的分割
- 拷贝和视图
-
- 完全不复制
- 视图或浅拷贝
- 深拷贝
- 功能和方法概述
- Less 基础
-
- 广播(Broadcasting)规则
- 花式索引和索引技巧
-
- 使用索引数组进行索引
- 使用布尔数组进行索引
- ix_()函数
-
- 简单数组操作
- 技巧和提示
-
- “自动”整形
- 矢量堆叠
- 直方图
- 数据类型
-
- 数组标量
- 溢出错误
- 扩展精度
- 创建数组
-
- 简介
- 将Python array_like对象转换为Numpy数组
- Numpy原生数组的创建
- 从磁盘读取数组
-
- 标准二进制格式
- 常见ASCII格式
- 自定义二进制格式
- 使用特殊库
- NumPy&Matplotlib
-
-
- 直线图
- 绘制正弦波
- subplot()
- bar()
- numpy.histogram()
- plt()
-
Numpy
%matplotlib inline
NumPy的主要对象是同构多维数组。它是一个元素表(通常是数字),所有类型都相同,由非负整数元组索引。在NumPy维度中称为轴。
import numpy as np
import torch
import sys
NumPy的数组类被调用ndarray。它也被别名所知 array。请注意,numpy.array这与标准Python库类不同array.array,后者只处理一维数组并提供较少的功能。ndarray对象更重要的属性是:
- ndarray.ndim - 数组的轴(维度)的个数。在Python世界中,维度的数量被称为rank。
- ndarray.shape - 数组的维度。这是一个整数的元组,表示每个维度中数组的大小。对于有 n 行和 m 列的矩阵,shape 将是 (n,m)。因此,shape 元组的长度就是rank或维度的个数 ndim。
- ndarray.size - 数组元素的总数。这等于 shape 的元素的乘积。
- ndarray.dtype - 一个描述数组中元素类型的对象。可以使用标准的Python类型创建或指定dtype。另外NumPy提供它自己的类型。例如numpy.int32、numpy.int16和numpy.float64。
- ndarray.itemsize - 数组中每个元素的字节大小。例如,元素为 float64 类型的数组的 itemsize 为8(=64/8),而 complex32 类型的数组的 itemsize 为4(=32/8)。它等于 ndarray.dtype.itemsize 。
- ndarray.data - 该缓冲区包含数组的实际元素。通常,我们不需要使用此属性,因为我们将使用索引访问数组中的元素
简单例子
b = torch.arange(15).reshape(3, 5)
b,b.type
(tensor([[ 0, 1, 2, 3, 4],
[ 5, 6, 7, 8, 9],
[10, 11, 12, 13, 14]]),
)
array1 = np.array([[1, 2, 3], [4, 5, 6]], dtype=np.float32) # array.dtype - 一个描述数组中元素类型的对象
a = np.arange(15).reshape(3, 5)
print(a)
print('数组的轴(维度)的个数:', a.ndim) # array.ndim - 数组的轴(维度)的个数
print('数组的维度:', a.shape) # array.shape - 数组的维度
print('数组元素的总数:', a.size) # array.size - 数组元素的总数
print('数组中每个元素的字节大小:', a.itemsize) # array.itemsize - 数组中每个元素的字节大小
print('数组中元素类型的对象:', a.dtype.name) # a.dtype.name
print('numpy于pytorch区分', type(a), type(b))
[[ 0 1 2 3 4]
[ 5 6 7 8 9]
[10 11 12 13 14]]
数组的轴(维度)的个数: 2
数组的维度: (3, 5)
数组元素的总数: 15
数组中每个元素的字节大小: 4
数组中元素类型的对象: int32
numpy于pytorch区分
-
得到的数组的类型是从Python列表中元素的类型推导出来的。
-
一个常见的错误,就是调用array的时候传入多个数字参数,而不是提供单个数字的列表类型作为参数。
a = np.array(1,2,3,4) # WRONG
a = np.array([1,2,3,4]) # RIGHT -
array 还可以将序列的序列转换成二维数组,将序列的序列的序列转换成三维数组,等等。
数组创建
也可以在创建时显式指定数组的类型:
a1 = np.array([[1, 2], [3, 4], [5, 6]], dtype=np.float64)
a1,a1.dtype,a1.dtype.name
(array([[1., 2.],
[3., 4.],
[5., 6.]]),
dtype('float64'),
'float64')
函数zeros创建一个由0组成的数组,函数 ones创建一个完整的数组,函数empty 创建一个数组,其初始内容是随机的,取决于内存的状态。默认情况下,创建的数组的dtype是 float64 类型的。
np.zeros((3, 4)),np.ones((3, 4), dtype=np.int64)'''''',np.empty((2, 3),dtype=np.float64) #未初始化,输出可能会发生变化
(array([[0., 0., 0., 0.],
[0., 0., 0., 0.],
[0., 0., 0., 0.]]),
array([[1, 1, 1, 1],
[1, 1, 1, 1],
[1, 1, 1, 1]], dtype=int64),
array([[0.3, 0.6, 0.9],
[1.2, 1.5, 1.8]]))
为了创建数字组成的数组,NumPy提供了一个类似于range的函数,该函数返回数组而不是列表
# 从第一个参数开始到第二个参数这个区间内,左闭右开,每个数据差第三个参数的大小,步长(step)
np.arange(10,30,5),np.arange(0,2,0.3) #它接受浮点参数
(array([10, 15, 20, 25]), array([0. , 0.3, 0.6, 0.9, 1.2, 1.5, 1.8]))
当arange与浮点参数一起使用时,由于有限的浮点精度,通常不可能预测所获得的元素的数量。出于这个原因,用 linspace 创建线段型数据,通常最好使用linspace函数来接收我们想要的元素数量的函数,而不是步长(step):
from numpy import pi
np.linspace(0,2,9) #从 0 到 2 的 9 个数字
array([0. , 0.25, 0.5 , 0.75, 1. , 1.25, 1.5 , 1.75, 2. ])
x=np.linspace(0,2*pi,100) #对在很多点评估功能很有用
f = np.sin(x)
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-3ioBb6Jp-1629463429281)(images/1.png)]
打印数组
当您打印数组时,NumPy以与嵌套列表类似的方式显示它,但具有以下布局:
- 最后一个轴从左到右打印,
- 倒数第二个从上到下打印,
- 其余部分也从上到下打印,每个切片用空行分隔。
然后将一维数组打印为行,将二维数据打印为矩阵,将三维数据打印为矩数组表。
a,a1
array([[ 0, 1, 2, 3, 4],
[ 5, 6, 7, 8, 9],
[10, 11, 12, 13, 14]])
c = np.arange(12).reshape(4,3,1)
c
array([[[ 0],
[ 1],
[ 2]],
[[ 3],
[ 4],
[ 5]],
[[ 6],
[ 7],
[ 8]],
[[ 9],
[10],
[11]]])
如果数组太大而无法打印,NumPy会自动跳过数组的中心部分并仅打印角点:
np.arange(10000),np.arange(10000).reshape(100,100)
(array([ 0, 1, 2, ..., 9997, 9998, 9999]),
array([[ 0, 1, 2, ..., 97, 98, 99],
[ 100, 101, 102, ..., 197, 198, 199],
[ 200, 201, 202, ..., 297, 298, 299],
...,
[9700, 9701, 9702, ..., 9797, 9798, 9799],
[9800, 9801, 9802, ..., 9897, 9898, 9899],
[9900, 9901, 9902, ..., 9997, 9998, 9999]]))
要禁用此行为并强制NumPy打印整个数组,可以使用更改打印选项set_printoptions
np.set_printoptions(threshold=sys.maxsize) #sys 模块应该被导入
基本操作
A = np.array([1,2,3])
B = np.arange(3)
A,B
(array([1, 2, 3]), array([0, 1, 2]))
C = A-B
C
array([1, 1, 1])
B*2
array([0, 2, 4])
B**2 #矩阵平方
array([0, 1, 4], dtype=int32)
10*np.sin(A) #10乘sin(A)中的所有元素
array([8.41470985, 9.09297427, 1.41120008])
A<35
array([ True, True, True]
与许多矩阵语言不同,乘积运算符*在NumPy数组中按元素进行运算。矩阵乘积可以使用@运算符(在python> = 3.5中)或dot函数或方法执行:
A*B #按元素进行运算
array([0, 2, 6])
A@B #矩阵乘积
8
A.dot(B)
8
x = np.array([[1,2],[3,4]])y = np.arange(4).reshape(2,2)x,y
(array([[1, 2], [3, 4]]), array([[0, 1], [2, 3]]))
x*y #按元素进行运算
array([[ 0, 2], [ 6, 12]])
x@y #矩阵乘积
array([[ 4, 7], [ 8, 15]])
x.dot(y) #矩阵乘积
array([[ 4, 7], [ 8, 15]])
某些操作(例如+=和 *=)会更直接更改被操作的矩阵数组而不会创建新矩阵数组。
a = np.ones((2,3),dtype=np.int64)a
array([[1, 1, 1], [1, 1, 1]], dtype=int64)
b = np.random.random((2,3))b
array([[0.26364226, 0.41650548, 0.75173233], [0.80333677, 0.51686147, 0.68512001]])
a *= 3a
array([[3, 3, 3], [3, 3, 3]], dtype=int64)
b += ab
array([[3.26364226, 3.41650548, 3.75173233], [3.80333677, 3.51686147, 3.68512001]])
a += b #b 不会自动转换为整数类型
---------------------------------------------------------------------------UFuncTypeError Traceback (most recent call last) in ----> 1 a += b
UFuncTypeError: Cannot cast ufunc 'add' output from dtype('float64') to dtype('int64') with casting rule 'same_kind'
当使用不同类型的数组进行操作时,结果数组的类型对应于更一般或更精确的数组(称为向上转换的行为)。
a = np.ones(3,dtype=np.int32)b = np.linspace(0,pi,3)a,b,a.dtype,b.dtype
(array([1, 1, 1]), array([0. , 1.57079633, 3.14159265]), dtype('int32'), dtype('float64'))
c=a+bc
array([1. , 2.57079633, 4.14159265])
c.dtype
dtype('float64')
d = np.exp(c*1j)d,d.dtype #新的复数类型(complex、complex64和complex128)简化了特定的数学操作。
(array([ 0.54030231+0.84147098j, -0.84147098+0.54030231j, -0.54030231-0.84147098j]), dtype('complex128'))
许多一元操作,例如计算数组中所有元素的总和,都是作为ndarray类的方法实现的。
a = np.random.random((2,3))a
array([[0.10327828, 0.17525785, 0.74043585], [0.38620688, 0.61422516, 0.35102992]])
a.sum()
2.3704339434850485
a.min(),a.max()
(0.10327827636483311, 0.7404358495396605)
默认情况下,这些操作适用于数组,就像它是一个数字列表一样,无论其形状如何。但是,通过指定axis 参数,您可以沿数组的指定轴应用操作:
b = np.arange(12).reshape(3,4)b
array([[ 0, 1, 2, 3], [ 4, 5, 6, 7], [ 8, 9, 10, 11]])
b.sum(axis=0),b.sum(axis=1) #0为列,1为行
(array([12, 15, 18, 21]), array([ 6, 22, 38]))
b.min(axis=0),b.min(axis=1),b.max(axis=0),b.max(axis=1)
(array([0, 1, 2, 3]), array([0, 4, 8]), array([ 8, 9, 10, 11]), array([ 3, 7, 11]))
Numpy中也具有cumsum()函数,其用法如下:
b.cumsum(),b.cumsum(axis=0),b.cumsum(axis=1) #将上一个(行,列)向下加合
(array([ 0, 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66], dtype=int32), array([[ 0, 1, 2, 3], [ 4, 6, 8, 10], [12, 15, 18, 21]], dtype=int32), array([[ 0, 1, 3, 6], [ 4, 9, 15, 22], [ 8, 17, 27, 38]], dtype=int32))
在cumsum()函数中:生成的每一项矩阵元素均是从原矩阵首项累加到对应项的元素之和。比如元素9,在cumsum()生成的矩阵中序号为3,即原矩阵中2,3,4三个元素的和。
相应的有累差运算函数:
print(np.diff(b))
该函数计算的便是每一行中后一项与前一项之差。故一个3行4列矩阵通过函数计算得到的矩阵便是3行3列的矩阵。
通函数
NumPy提供熟悉的数学函数,例如sin,cos和exp。在NumPy中,这些被称为“通函数”(ufunc)。在NumPy中,这些函数在数组上按元素进行运算,产生一个数组作为输出。
b = np.arange(3)
b
array([0, 1, 2])
np.exp(b) #指数
array([1. , 2.71828183, 7.3890561 ])
np.sqrt(b) #平方
array([0. , 1. , 1.41421356])
c = np.array([1,2,3])
np.add(b,c)
(array([1, 3, 5]), array([1, 3, 5]))
索引、切片和迭代
一维的数组可以进行索引、切片和迭代操作的,就像 列表 和其他Python序列类型一样。
a = np.arange(10)**3
a,a[2],a[2:5] #一般都是左闭右开
(array([ 0, 1, 8, 27, 64, 125, 216, 343, 512, 729], dtype=int32),
8,
array([ 8, 27, 64], dtype=int32))
a[:6:2] = -1000 #等同于a[0:6:2] = -1000,从开始到位置 6,将每第二个元素设置为 -1000
a
array([-1000, 1, -1000, 27, -1000, 125, 216, 343, 512,
729], dtype=int32)
a[ : :-1] #颠倒数组,倒置
array([ 729, 512, 343, 216, 125, -1000, 27, -1000, 1,
-1000], dtype=int32)
for i in a:
print(i**(1/3.))
nan
1.0
nan
3.0
nan
5.0
5.999999999999999
6.999999999999999
7.999999999999999
8.999999999999998
:2: RuntimeWarning: invalid value encountered in power
print(i**(1/3.))
多维的数组每个轴可以有一个索引。这些索引以逗号分隔的元组给出:
def f(x,y):
return 10*x+y
b = np.fromfunction(f,(5,4),dtype=int)
b,b[2,3],b[0:5,1],b[:,1],b[1:3,:]
(array([[ 0, 1, 2, 3],
[10, 11, 12, 13],
[20, 21, 22, 23],
[30, 31, 32, 33],
[40, 41, 42, 43]]),
23,
array([ 1, 11, 21, 31, 41]),
array([ 1, 11, 21, 31, 41]),
array([[10, 11, 12, 13],
[20, 21, 22, 23]]))
当提供的索引少于轴的数量时,缺失的索引被认为是完整的切片:
b[-1]
array([40, 41, 42, 43])
b[i] 方括号中的表达式 i 被视为后面紧跟着 : 的多个实例,用于表示剩余轴。NumPy也允许你使用三个点写为 b[i,…]。
三个点( … )表示产生完整索引元组所需的冒号。例如,如果 x 是rank为5的数组(即,它具有5个轴),则:
- x[1,2,…] 相当于 x[1,2,:,:,:],
- x[…,3] 等效于 x[:,:,:,:,3]
- x[4,…,5,:] 等效于 x[4,:,:,5,:]。
c = np.array([[[0,1,2],[10,12,13]],[[100,101,102],[110,112,113]]])
c.shape
(2, 2, 3)
c[1,...] #与 c[1,:,:] 或 c[1] 相同
array([[100, 101, 102],
[110, 112, 113]])
c[...,2] #与 c[:,:,2] 相同
array([[ 2, 13], [102, 113]])
对多维数组进行 迭代(Iterating) 是相对于第一个轴完成的:
for row in b: print(row)
[0 1 2 3][10 11 12 13][20 21 22 23][30 31 32 33][40 41 42 43]
如果想要对数组中的每个元素执行操作,可以使用flat属性,该属性是数组的所有元素的迭代器:
for element in b.flat: print(element)
012310111213202122233031323340414243
形状操纵
改变数组的形状
一个数组的形状是由每个轴的元素数量决定的:
a = np.floor(10*np.random.random((3,4)))aa.shape
(3, 4)
a.ravel() #返回数组,扁平化
array([0., 9., 7., 1., 1., 4., 3., 7., 5., 9., 5., 2.])
a.reshape(6,2) #返回具有修改形状的数组
array([[0., 9.], [7., 1.], [1., 4.], [3., 7.], [5., 9.], [5., 2.]])
a.T #返回数组,转置
array([[0., 1., 5.], [9., 4., 9.], [7., 3., 5.], [1., 7., 2.]])
a.T.shape ,a.shape
((4, 3), (3, 4))
由 ravel()产生的数组中元素的顺序通常是“C风格”,也就是说,最右边的索引“变化最快”,因此[0,0]之后的元素是[0,1] 。如果将数组重新整形为其他形状,则该数组将被视为“C风格”。NumPy通常创建按此顺序存储的数组,因此 ravel() 通常不需要复制其参数,但如果数组是通过获取另一个数组的切片或使用不常见的选项创建的,则可能需要复制它。还可以使用可选参数指示函数 ravel() 和 reshape(),以使用FORTRAN样式的数组,其中最左边的索引变化最快。
该reshape函数返回带有修改形状的参数,而该 ndarray.resize方法会修改数组本身:
a
array([[0., 9., 7., 1.], [1., 4., 3., 7.], [5., 9., 5., 2.]])
a.resize((2,6))a
array([[0., 9., 7., 1., 1., 4.], [3., 7., 5., 9., 5., 2.]])
如果在 reshape 操作中将 size 指定为-1,则会自动计算其他的 size 大小:
a.reshape(3,-1)
array([[0., 9., 7., 1.], [1., 4., 3., 7.], [5., 9., 5., 2.]])
将不同数组堆叠在一起
几个数组可以沿不同的轴堆叠在一起,例如:
a = np.floor(10*np.random.random((2,2)))a
array([[9., 1.], [8., 0.]])
b = np.floor(10*np.random.random((2,2)))b
array([[4., 9.], [3., 1.]])
np.vstack((a,b)),np.hstack((a,b)) #vstack上下堆叠,hstack左右堆叠
(array([[9., 1.], [8., 0.], [4., 9.], [3., 1.]]), array([[9., 1., 4., 9.], [8., 0., 3., 1.]]))
np.newaxis的作用就是选取部分的数据增加一个维度
array=random.rand(4,4)
array([[0.45284467, 0.27883581, 0.72870975, 0.03455946], [0.74005136, 0.52413785, 0.78433733, 0.80114353], [0.16559874, 0.56112999, 0.18464461, 0.38968731], [0.05684794, 0.50929997, 0.45789637, 0.63199181]])
array_add_aix=array[:,np.newaxis]
array([[[0.45284467, 0.27883581, 0.72870975, 0.03455946]], [[0.74005136, 0.52413785, 0.78433733, 0.80114353]], [[0.16559874, 0.56112999, 0.18464461, 0.38968731]], [[0.05684794, 0.50929997, 0.45789637, 0.63199181]]])
以上是默认选取全部的数据进行增加维度,还可以选取部分的数据增加维度:
>>> array_add_axis=array[0:2,np.newaxis]>>> array_add_axisarray([[[0.45284467, 0.27883581, 0.72870975, 0.03455946]], [[0.74005136, 0.52413785, 0.78433733, 0.80114353]]])
该函数将column_stack 1D数组作为列堆叠到2D数组中。它仅相当于 hstack2D数组:
from numpy import newaxis np.column_stack((a,b))
array([[9., 1., 4., 9.], [8., 0., 3., 1.]])
a = np.array([4.,2.])b = np.array([3.,8.])np.column_stack((a,b)) # 返回一个二维数组
array([[4., 3.], [2., 8.]])
np.hstack((a,b)),np.vstack((a,b))
(array([4., 2., 3., 8.]), array([[4., 2.], [3., 8.]]))
a[:,newaxis],b[:,newaxis]
(array([[4.], [2.]]), array([[3.], [8.]]))
np.column_stack((a[:,newaxis],b[:,newaxis])),np.hstack((a[:,newaxis],b[:,newaxis]))
(array([[4., 3.], [2., 8.]]), array([[4., 3.], [2., 8.]]))
另一方面,该函数ma.row_stack等效vstack 于任何输入数组。通常,对于具有两个以上维度的数组, hstack沿其第二轴vstack堆叠,沿其第一轴堆叠,并concatenate 允许可选参数给出连接应发生的轴的编号。
当你的合并操作需要针对多个矩阵或序列时,借助concatenate函数可能会让你使用起来比前述的函数更加方便:
C = np.concatenate((A,B,B,A),axis=0)C
array([[1], [1], [1], [2], [2], [2], [2], [2], [2], [1], [1], [1]])
D = np.concatenate((A,B,B,A),axis=1)D
array([[1, 2, 2, 1], [1, 2, 2, 1], [1, 2, 2, 1]])
axis参数很好的控制了矩阵的纵向或是横向打印,相比较vstack和hstack函数显得更加方便。
注意
在复杂的情况下,r_和c_于通过沿一个轴堆叠数字来创建数组很有用。它们允许使用范围操作符(“:”)。
np.r_[1:4,0,4]
array([1, 2, 3, 0, 4])
将一个数组拆分成几个较小的数组(分割)
纵向分割
A = np.arange(12).reshape((3, 4))np.split(A, 2, axis=1)
[array([[0, 1], [4, 5], [8, 9]]), array([[ 2, 3], [ 6, 7], [10, 11]])]
横向分割
np.split(A, 3, axis=0)
[array([[0, 1, 2, 3]]), array([[4, 5, 6, 7]]), array([[ 8, 9, 10, 11]])]
错误的分割
范例的Array只有4列,只能等量对分,因此输入以上程序代码后Python就会报错。
np.split(A, 3, axis=1)
# ValueError: array split does not result in an equal division
为了解决这种情况, 我们会有下面这种方式.
不等量的分割
在机器学习时经常会需要将数据做不等量的分割,因此解决办法为np.array_split()
np.array_split(A, 3, axis=1)
[array([[0, 1], [4, 5], [8, 9]]), array([[ 2], [ 6], [10]]), array([[ 3], [ 7], [11]])]
使用hsplit,可以沿数组的水平轴拆分数组,方法是指定要返回的形状相等的数组的数量,或者指定应该在其之后进行分割的列:
a = np.floor(10*np.random.random((2,12)))a
array([[4., 6., 4., 6., 6., 3., 5., 0., 0., 6., 3., 7.], [8., 9., 0., 5., 8., 1., 7., 7., 7., 9., 2., 9.]])
np.hsplit(a,3) # 将 a 拆分为 3部分
[array([[4., 6., 4., 6.], [8., 9., 0., 5.]]), array([[6., 3., 5., 0.], [8., 1., 7., 7.]]), array([[0., 6., 3., 7.], [7., 9., 2., 9.]])]
np.hsplit(a,(3,4)) #在第三和第四列之后拆分 a
[array([[4., 6., 4.], [8., 9., 0.]]), array([[6.], [5.]]), array([[6., 3., 5., 0., 0., 6., 3., 7.], [8., 1., 7., 7., 7., 9., 2., 9.]])]
vsplit沿垂直轴分割,并array_split允许指定要分割的轴。
拷贝和视图
当计算和操作数组时,有时会将数据复制到新数组中,有时则不会。这通常是初学者混淆的根源。有三种情况:
完全不复制
简单分配不会复制数组对象或其数据。
a = np.arange(12)a
array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11])
b = a #没有创建新对象b
array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11])
b is a,a.shape
(True, (12,))
b.shape = 3,4 #改变a的形状a.shape
(3, 4)
Python将可变对象作为引用传递,因此函数调用不会复制。
def f(x): print(id(x)) id(a),f(a) #id 是对象的唯一标识符
1833900046576(1833900046576, None)
视图或浅拷贝
不同的数组对象可以共享相同的数据。该view方法创建一个查看相同数据的新数组对象。
c = a.view() #c是a拥有的数据的视图c,c is a ,c.base is a
(array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]]),
False,
True)
c.flags.owndata
False
c.shape = 2,6 #a 的形状不会改变
a.shape
(3, 4)
c[0,4] = 1234
a
array([[ 0, 1, 2, 3],
[1234, 5, 6, 7],
[ 8, 9, 10, 11]])
切片数组会返回一个视图:
s = a[ : , 1:3] #为清晰起见添加了空格; 也可以写成“s = a[:,1:3]”
s
array([[ 1, 2],
[ 5, 6],
[ 9, 10]])
s[:]=10 #s[:] 是 s 的一个视图。 注意 s=10 和 s[:]=10 的区别
s,a
(array([[10, 10],
[10, 10],
[10, 10]]),
array([[ 0, 10, 10, 3],
[1234, 10, 10, 7],
[ 8, 10, 10, 11]]))
深拷贝
该copy方法生成数组及其数据的完整副本。
d = a.copy() #创建一个带有新数据的新数组对象
d is a,d.base is a #d 不与 a 共享任何东西
(False, False)
d[0,0] =111
a
array([[ 0, 10, 10, 3],
[1234, 10, 10, 7],
[ 8, 10, 10, 11]])
有时,如果不再需要原始数组,则应在切片后调用 copy。例如,假设a是一个巨大的中间结果,最终结果b只包含a的一小部分,那么在用切片构造b时应该做一个深拷贝:
a = np.arange(int(1e8))
b = a[:100].copy()
del a #可以释放``a`` 的内存。
如果改为使用 b = a[:100],则 a 由 b 引用,并且即使执行 del a 也会在内存中持久存在。
功能和方法概述
以下是按类别排序的一些有用的NumPy函数和方法名称的列表。有关完整列表,请参阅参考手册里的常用API。
- 数组的创建(Array Creation) - arange, array, copy, empty, empty_like, eye, fromfile, fromfunction, identity, linspace, logspace, mgrid, ogrid, ones, ones_like, zeros, zeros_like
- 转换和变换(Conversions) - ndarray.astype, atleast_1d, atleast_2d, atleast_3d, mat
- 操纵术(Manipulations) - array_split, column_stack, concatenate, diagonal, dsplit, dstack, hsplit, hstack, ndarray.item, newaxis, ravel, repeat, reshape, resize, squeeze, swapaxes, take, transpose, vsplit, vstack
- 询问(Questions) - all, any, nonzero, where,
- 顺序(Ordering) - argmax, argmin, argsort, max, min, ptp, searchsorted, sort
- 操作(Operations) - choose, compress, cumprod, cumsum, inner, ndarray.fill, imag, prod, put, putmask, real, sum
- 基本统计(Basic Statistics) - cov, mean, std, var
- 基本线性代数(Basic Linear Algebra) - cross, dot, outer, linalg.svd, vdot
nonzero()函数:
1
A = np.arange(2,14).reshape((3,4))
# array([[ 2, 3, 4, 5]
# [ 6, 7, 8, 9]
# [10,11,12,13]])
print(np.nonzero(A))
(array([0,0,0,0,1,1,1,1,2,2,2,2]),array([0,1,2,3,0,1,2,3,0,1,2,3]))
这个函数将所有非零元素的行与列坐标分割开,重构成两个分别关于行和列的矩阵。
Less 基础
广播(Broadcasting)规则
广播允许通用功能以有意义的方式处理不具有完全相同形状的输入。
广播的第一个规则是,如果所有输入数组不具有相同数量的维度,则将“1”重复地预先添加到较小数组的形状,直到所有数组具有相同数量的维度。
广播的第二个规则确保沿特定维度的大小为1的数组表现为具有沿该维度具有最大形状的数组的大小。假定数组元素的值沿着“广播”数组的那个维度是相同的。
应用广播规则后,所有数组的大小必须匹配。更多细节可以在广播中找到。
花式索引和索引技巧
NumPy提供比常规Python序列更多的索引功能。除了通过整数和切片进行索引之外,正如我们之前看到的,数组可以由整数数组和布尔数组索引。
使用索引数组进行索引
数组与索引数组维度相同
a = np.arange(12)**2 #前 12 个数的平方i = np.array([1,1,3,8,5]) #索引数组a,a[i] #a 在位置 i 的元素
(array([ 0, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121], dtype=int32), array([ 1, 1, 9, 64, 25], dtype=int32))
j = np.array( [ [ 3, 4], [ 9, 7 ] ] ) #一个二维索引数组a[j] #与 j 的形状相同
array([[ 9, 16], [81, 49]], dtype=int32)
当索引数组a是多维的时,单个索引数组指的是第一个维度a。以下示例通过使用调色板将标签图像转换为彩色图像来显示此行为。
palette = np.array([[0,0,0], [255,0,0], [0,255,0], [0,0,255], [255,255,255]])palette
array([[ 0, 0, 0], [255, 0, 0], [ 0, 255, 0], [ 0, 0, 255], [255, 255, 255]])
image = np.array([[0,1,2,0],[0,3,4,0]]) #每个值对应于调色板中的一种颜色image
array([[0, 1, 2, 0], [0, 3, 4, 0]])
palette[image] #(2,4,3) 彩色图像
array([[[ 0, 0, 0], [255, 0, 0], [ 0, 255, 0], [ 0, 0, 0]], [[ 0, 0, 0], [ 0, 0, 255], [255, 255, 255], [ 0, 0, 0]]])
我们还可以为多个维度提供索引。每个维度的索引数组必须具有相同的形状。
a = np.arange(12).reshape(3,4)a
array([[ 0, 1, 2, 3], [ 4, 5, 6, 7], [ 8, 9, 10, 11]])
i = np.array([[0,1],[1,2]])j = np.array([[2,1],[3,3]])a[i,j] #每个索引各出一个值
array([[ 2, 5], [ 7, 11]])
a[i,2],a[:,j]
(array([[ 2, 6], [ 6, 10]]), array([[[ 2, 1], [ 3, 3]], [[ 6, 5], [ 7, 7]], [[10, 9], [11, 11]]]))
当然,我们可以按顺序(比如列表)放入i,j然后使用列表进行索引。
l = [i,j]l
[array([[0, 1], [1, 2]]), array([[2, 1], [3, 3]])]
但是,我们不能通过放入i和j放入数组来实现这一点,因为这个数组将被解释为索引a的第一个维度。所以tuple(l)来避免错误
a[tuple(l)] #防止出错
array([[ 2, 5], [ 7, 11]])
argmin() 和 argmax() 两个函数分别对应着求矩阵中最小元素和最大元素的索引。使用数组索引的另一个常见用法是搜索与时间相关的系列的最大值:
time = np.linspace(20, 145, 5) data = np.sin(np.arange(20)).reshape(5,4) time,data
(array([ 20. , 51.25, 82.5 , 113.75, 145. ]), array([[ 0. , 0.84147098, 0.90929743, 0.14112001], [-0.7568025 , -0.95892427, -0.2794155 , 0.6569866 ], [ 0.98935825, 0.41211849, -0.54402111, -0.99999021], [-0.53657292, 0.42016704, 0.99060736, 0.65028784], [-0.28790332, -0.96139749, -0.75098725, 0.14987721]]))
ind = data.argmax(axis=0) #每个系列的最大值索引ind
array([2, 0, 3, 1], dtype=int64)
time_max = time[ind] #???data_max = data[ind, range(data.shape[1])] # => data[ind[0],0], data[ind[1],1]...time_max,data_max
(array([ 82.5 , 20. , 113.75, 51.25]), array([0.98935825, 0.84147098, 0.99060736, 0.6569866 ]))
np.all(data_max == data.max(axis=0))
True
您还可以使用数组索引作为分配给的目标:
a = np.arange(5)a
array([0, 1, 2, 3, 4])
a[[1,3,4]]=0a
array([0, 0, 2, 0, 0])
当索引列表包含重复时,分配会多次完成,留下最后一个值:
a = np.arange(5)a[[0,0,2]]=[1,2,3]a
array([2, 1, 3, 3, 4])
是否要使用Python的 +=构造,因为它可能不会按预期执行:
a = np.arange(5)a[[0,0,2]]+=1a
array([1, 1, 3, 3, 4])
即使0在索引列表中出现两次,第0个元素也只增加一次。这是因为Python要求“a + = 1”等同于“a = a + 1”。
如果需要计算统计中的均值,可以利用下面的方式,将整个矩阵的均值求出来:
a = np.arange(3, 15).reshape((3, 4))
array([[ 3, 4, 5, 6], [ 7, 8, 9, 10], [11, 12, 13, 14]])
print(np.mean(a)) # 8.5
print(np.average(a)) # 8.5
仿照着前一节中dot() 的使用法则,mean()函数还有另外一种写法:
print(a.mean()) # 8.5
同样的,我们可以写出求解中位数的函数:
print(a.median()) # 7.5
关于迭代输出的问题:
A = np.arange(3,15).reshape((3,4))print(A.flatten())
# array([3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14])
for item in A.flat: print(item)
34567891011121314
这一脚本中的flatten是一个展开性质的函数,将多维的矩阵进行展开成1行的数列。而flat是一个迭代器,本身是一个object属性。
使用布尔数组进行索引
当我们使用(整数)索引数组索引数组时,我们提供了要选择的索引列表。使用布尔索引,方法是不同的; 我们明确地选择我们想要的数组中的哪些项目以及我们不需要的项目。
人们可以想到的最自然的布尔索引方法是使用与原始数组具有 相同形状的 布尔数组:
a = np.arange(12).reshape(3,4)b = a > 4b #b 是具有 a 形状的布尔值
array([[False, False, False, False], [False, True, True, True], [ True, True, True, True]])
a[b] #具有选定元素的一维数组
array([ 5, 6, 7, 8, 9, 10, 11])
a[b] = 0 #'a' 中大于 4 的所有元素都变为 0a
array([[0, 1, 2, 3],
[4, 0, 0, 0],
[0, 0, 0, 0]])
使用布尔索引生成Mandelbrot集的图像:
import matplotlib.pyplot as plt
def mandelbrot(h,w,maxit=20):
'''返回大小为 (h,w) 的 Mandelbrot 分形图像'''
y,x = np.ogrid[ -1.4:1.4:h*1j, -2:0.8:w*1j ]
c = x+y*1j
z = c
divtime = maxit + np.zeros(z.shape, dtype=int)
for i in range(maxit):
z = z**2 + c
diverge = z*np.conj(z) > 2**2 #谁在发散
div_now = diverge & (divtime==maxit) #现在谁在发散
divtime[div_now] = i #注意什么时候
z[diverge] = 2 #避免发散太多
return divtime
plt.imshow(mandelbrot(400,400))
plt.show()
使用布尔值进行索引的第二种方法更类似于整数索引; 对于数组的每个维度,我们给出一个1D布尔数组,选择我们想要的切片:
a = np.arange(12).reshape(3,4)
b1 = np.array([False,True,True])
b2 = np.array([True,False,True,False])
a[b1,:] #选择行
array([[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
a[b1] #选择行
array([[ 4, 5, 6, 7], [ 8, 9, 10, 11]])
a[:,b2] #选择列
array([[ 0, 2], [ 4, 6], [ 8, 10]])
a[b1,b2]
array([ 4, 10])
请注意,1D布尔数组的长度必须与要切片的尺寸(或轴)的长度一致。在前面的例子中,b1具有长度为3(的数目 的行 中a),和 b2(长度4)适合于索引的第二轴线(列) a。
ix_()函数
ix_函数可用于组合不同的向量,以便获得每个n-uplet的结果。例如,如果要计算从每个向量a,b和c中取得的所有三元组的所有a + b * c:
a = np.array([2,3,4,5])
b = np.array([8,5,4])
c = np.array([5,4,6,8,3])
ax,bx,cx = np.ix_(a,b,c)
ax,bx,cx
(array([[[2]],
[[3]],
[[4]],
[[5]]]),
array([[[8],
[5],
[4]]]),
array([[[5, 4, 6, 8, 3]]]))
ax.shape, bx.shape, cx.shape
((4, 1, 1), (1, 3, 1), (1, 1, 5))
result = ax+bx*cx
result,a,b,c
(array([[[42, 34, 50, 66, 26],
[27, 22, 32, 42, 17],
[22, 18, 26, 34, 14]],
[[43, 35, 51, 67, 27],
[28, 23, 33, 43, 18],
[23, 19, 27, 35, 15]],
[[44, 36, 52, 68, 28],
[29, 24, 34, 44, 19],
[24, 20, 28, 36, 16]],
[[45, 37, 53, 69, 29],
[30, 25, 35, 45, 20],
[25, 21, 29, 37, 17]]]),
array([2, 3, 4, 5]),
array([8, 5, 4]),
array([5, 4, 6, 8, 3]))
result[3,2,4]
17
a[3]+b[2]*c[4]
17
def ufunc_reduce(ufct, *vectors):
vs = np.ix_(*vectors)
r = ufct.identity
for v in vs:
r = ufct(r,v)
return r
ufunc_reduce(np.add,a,b,c) #交叉索引必须是一维的
array([[[15, 14, 16, 18, 13],
[12, 11, 13, 15, 10],
[11, 10, 12, 14, 9]],
[[16, 15, 17, 19, 14],
[13, 12, 14, 16, 11],
[12, 11, 13, 15, 10]],
[[17, 16, 18, 20, 15],
[14, 13, 15, 17, 12],
[13, 12, 14, 16, 11]],
[[18, 17, 19, 21, 16],
[15, 14, 16, 18, 13],
[14, 13, 15, 17, 12]]])
与普通的ufunc.reduce相比,这个版本的reduce的优点是它利用了广播规则 ,以避免创建一个参数数组,输出的大小乘以向量的数量。
简单数组操作
a = np.array([[1.0, 2.0], [3.0, 4.0]])a
array([[1., 2.], [3., 4.]])
a.transpose(),a.T #转置 pirnt(np.transpose(a))
(array([[1., 3.], [2., 4.]]), array([[1., 3.], [2., 4.]]))
np.linalg.inv(a) #矩阵求逆 ,np.linalg.det():矩阵求行列式(标量)
array([[-2. , 1. ], [ 1.5, -0.5]])
函数的原型:numpy.eye(N,M=None,k=0,dtype=
返回的是一个二维2的数组(N,M),对角线的地方为1,其余的地方为0.
参数介绍:
(1)N:int型,表示的是输出的行数
(2)M:int型,可选项,输出的列数,如果没有就默认为N
(3)k:int型,可选项,对角线的下标,默认为0表示的是主对角线,负数表示的是低对角,正数表示的是高对角。
(4)dtype:数据的类型,可选项,返回的数据的数据类型
(5)order:{‘C’,‘F’},可选项,也就是输出的数组的形式是按照C语言的行优先’C’,还是按照
u = np.eye(2) u
array([[1., 0.], [0., 1.]])
j = np.array([[0.0, -1.0], [1.0, 0.0]])j @ j
array([[-1., 0.], [ 0., -1.]])
np.trace(u) #????
2.0
y = np.array([[5.], [7.]])np.linalg.solve(a, y)
array([[-3.], [ 4.]])
np.linalg.eig(j) #求矩阵的特征值与特征向量(np.linalg.eig)
(array([0.+1.j, 0.-1.j]), array([[0.70710678+0.j , 0.70710678-0.j ], [0. -0.70710678j, 0. +0.70710678j]]))
技巧和提示
“自动”整形
要更改数组的尺寸,您可以省略其中一个尺寸,然后自动推导出尺寸:
a = np.arange(30)a.shape = 2,-1,3a.shape,a
((2, 5, 3), array([[[ 0, 1, 2], [ 3, 4, 5], [ 6, 7, 8], [ 9, 10, 11], [12, 13, 14]], [[15, 16, 17], [18, 19, 20], [21, 22, 23], [24, 25, 26], [27, 28, 29]]]))
同样的,我们可以对所有元素进行仿照列表一样的排序操作,但这里的排序函数仍然仅针对每一行进行从小到大排序操作:
A = np.arange(2,14).reshape((3,4))
# array([[ 2, 3, 4, 5]
# [ 6, 7, 8, 9]
# [10,11,12,13]])
A = np.arange(14,2, -1).reshape((3,4))
array([[14, 13, 12, 11],
[10, 9, 8, 7],
[ 6, 5, 4, 3]])
print(np.sort(A))
array([[11,12,13,14]
[ 7, 8, 9,10]
[ 3, 4, 5, 6]])
在Numpy中具有clip()函数,例子如下:
print(A)
# array([[14,13,12,11]
# [10, 9, 8, 7]
# [ 6, 5, 4, 3]])
print(np.clip(A,5,9))
# array([[ 9, 9, 9, 9]
# [ 9, 9, 8, 7]
# [ 6, 5, 5, 5]])
这个函数的格式是clip(Array,Array_min,Array_max),顾名思义,Array指的是将要被执行用的矩阵,而后面的最小值最大值则用于让函数判断矩阵中元素是否有比最小值小的或者比最大值大的元素,并将这些指定的元素转换为最小值或者最大值。
矢量堆叠
我们如何从同等大小的行向量列表中构造一个二维数组?在MATLAB这是很简单:如果x和y你只需要做两个相同长度的向量m=[x;y]。在此NumPy的通过功能的工作原理column_stack,dstack,hstack和vstack,视维在堆叠是必须要做的。
vertical stack本身属于一种上下合并,即对括号中的两个整体进行对应操作。例如:
x = np.arange(0,10,2)
y = np.arange(5)
m = np.vstack([x,y])
xy = np.hstack([x,y])
x,y,m,xy
(array([0, 2, 4, 6, 8]),
array([0, 1, 2, 3, 4]),
array([[0, 2, 4, 6, 8],
[0, 1, 2, 3, 4]]),
array([0, 2, 4, 6, 8, 0, 1, 2, 3, 4]))
直方图
histogram应用于数组的NumPy 函数返回一对向量:数组的直方图和bin的向量。注意: matplotlib还有一个构建直方图的功能(hist在Matlab中称为),与NumPy中的直方图不同。主要区别在于pylab.hist自动绘制直方图,而 numpy.histogram只生成数据。
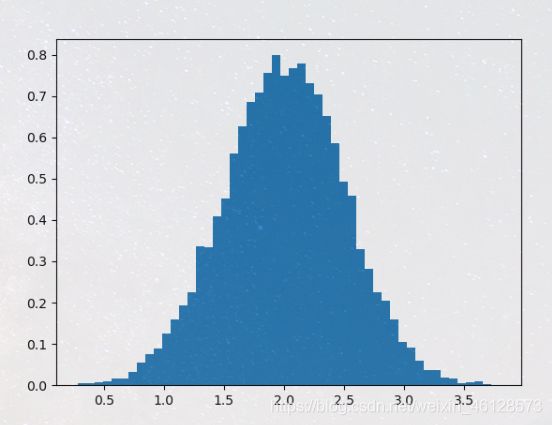
import matplotlib.pyplot as plt'''构建一个包含 10000 个正态偏差的向量,方差为 0.5^2,均值为 2'''mu, sigma = 2, 0.5v = np.random.normal(mu,sigma,10000)'''绘制具有 50 个 bin 的归一化直方图'''plt.hist(v, bins=50, density=1) plt.show()
'''用 numpy 计算直方图,然后绘制它'''(n, bins) = np.histogram(v, bins=50, density=True)plt.plot(.5*(bins[1:]+bins[:-1]), n)plt.show()
数据类型
x = np.float32(1.0)y = np.int_([1,2,4])z = np.arange(3, dtype=np.uint8)x,y,z
(1.0, array([1, 2, 4]), array([0, 1, 2], dtype=uint8))
np.array([1, 2, 3], dtype='f')
array([1., 2., 3.], dtype=float32)
z.astype(float)
array([0., 1., 2.])
np.int8(z),z.dtype
(array([0, 1, 2], dtype=int8), dtype('uint8'))
NumPy的人都知道int是指np.int_,bool意味着np.bool_,这float是np.float_和complex是np.complex_。其他数据类型没有Python等价物。
dtype对象还包含有关类型的信息,例如其位宽和字节顺序。数据类型也可以间接用于查询类型的属性,例如它是否为整数:
d = np.dtype(int)d,np.issubdtype(d, np.integer),np.issubdtype(d, np.floating)
(dtype('int32'), True, False)
数组标量
NumPy通常将数组元素作为数组标量返回(带有关联dtype的标量)。数组标量与Python标量不同,但在大多数情况下它们可以互换使用(主要的例外是早于v2.x的Python版本,其中整数数组标量不能作为列表和元组的索引)。有一些例外,例如当代码需要标量的非常特定的属性或者它特定地检查值是否是Python标量时。通常,存在的问题很容易被显式转换数组标量到Python标量,采用相应的Python类型的功能(例如,固定的int,float,complex,str,unicode)。
使用数组标量的主要优点是它们保留了数组类型(Python可能没有匹配的标量类型,例如int16)。因此,使用数组标量可确保数组和标量之间的相同行为,无论值是否在数组内。NumPy标量也有许多与数组相同的方法。
溢出错误
当值需要比数据类型中的可用内存更多的内存时,NumPy数值类型的固定大小可能会导致溢出错误。例如,numpy.power对于64位整数正确计算 100 * 10 * 8,但对于32位整数给出1874919424(不正确)。
>>> np.power(100, 8, dtype=np.int64)
10000000000000000
>>> np.power(100, 8, dtype=np.int32)
1874919424
NumPy和Python整数类型的行为在整数溢出方面存在显着差异,并且可能会使用户期望NumPy整数的行为类似于Python int。与 NumPy 不同,Python 的大小int 是灵活的。这意味着Python整数可以扩展以容纳任何整数并且不会溢出。
NumPy分别提供numpy.iinfo并numpy.finfo验证NumPy整数和浮点值的最小值或最大值:
>>> np.iinfo(np.int) # Bounds of the default integer on this system.
iinfo(min=-9223372036854775808, max=9223372036854775807, dtype=int64)
>>> np.iinfo(np.int32) # Bounds of a 32-bit integer
iinfo(min=-2147483648, max=2147483647, dtype=int32)
>>> np.iinfo(np.int64) # Bounds of a 64-bit integer
iinfo(min=-9223372036854775808, max=9223372036854775807, dtype=int64)
如果64位整数仍然太小,则结果可能会转换为浮点数。浮点数提供了更大但不精确的可能值范围。
>>> np.power(100, 100, dtype=np.int64) # Incorrect even with 64-bit int
0
>>> np.power(100, 100, dtype=np.float64)
1e+200
扩展精度
Python 的浮点数通常是64位浮点数,几乎等同于 np.float64 。在某些不寻常的情况下,使用更精确的浮点数可能会很有用。这在numpy中是否可行取决于硬件和开发环境:具体地说,x86机器提供80位精度的硬件浮点,虽然大多数C编译器提供这一点作为它们的 long double 类型,MSVC(Windows构建的标准)使 long double 等同于 double (64位)。NumPy使编译器的 long double 作为 np.longdouble 可用(而 np.clongdouble 用于复数)。您可以使用 np.finfo(np.longdouble) 找出 numpy提供了什么。
NumPy不提供比C的 long double 更高精度的dtype;特别是128位IEEE四精度数据类型(FORTRAN的 REAL*16 )不可用。
为了有效地进行内存的校准,np.longdouble通常以零位进行填充,即96或者128位, 哪个更有效率取决于硬件和开发环境;通常在32位系统上它们被填充到96位,而在64位系统上它们通常被填充到128位。np.longdouble被填充到系统默认值;为需要特定填充的用户提供了np.float96和np.float128。尽管它们的名称是这样叫的, 但是np.float96和np.float128只提供与np.longdouble一样的精度, 即大多数x86机器上的80位和标准Windows版本中的64位。
请注意,即使np.longdouble提供比python float更多的精度,也很容易失去额外的精度,因为python通常强制值通过float传递值。例如,%格式操作符要求将其参数转换为标准python类型,因此即使请求了许多小数位,也不可能保留扩展精度。使用值1 + np.finfo(np.longdouble).eps测试你的代码非常有用。
创建数组
简介
创建数组有5种常规机制:
- 从其他Python结构(例如,列表,元组)转换
- numpy原生数组的创建(例如,arange、ones、zeros等)
- 从磁盘读取数组,无论是标准格式还是自定义格式
- 通过使用字符串或缓冲区从原始字节创建数组
- 使用特殊库函数(例如,random)
本节不包括复制,连接或以其他方式扩展或改变现有数组的方法。它也不会涵盖创建对象数组或结构化数组。这些都包含在他们自己的章节中。
将Python array_like对象转换为Numpy数组
通常,在Python中排列成array-like结构的数值数据可以通过使用array()函数转换为数组。最明显的例子是列表和元组。有关其使用的详细信息,请参阅array()的文档。一些对象可能支持数组协议并允许以这种方式转换为数组。找出对象是否可以使用array()转换为一个数组numpy 数组的简单方法很简单,只要交互式试一下,看看它是否工作!(Python方式)。
>>> x = np.array([2,3,1,0])
>>> x = np.array([2, 3, 1, 0])
>>> x = np.array([[1,2.0],[0,0],(1+1j,3.)]) # note mix of tuple and lists,
and types
>>> x = np.array([[ 1.+0.j, 2.+0.j], [ 0.+0.j, 0.+0.j], [ 1.+1.j, 3.+0.j]])
Numpy原生数组的创建
Numpy内置了从头开始创建数组的函数:
zeros(shape)将创建一个用指定形状用0填充的数组。默认的dtype是float64。
np.zeros((2,3))
array([[0., 0., 0.],
[0., 0., 0.]])
ones(shape)将创建一个用1个值填充的数组。它在所有其他方面与zeros相同。
arange()将创建具有有规律递增值的数组。检查文档字符串以获取有关可以使用的各种方式的完整信息。这里给出几个例子:
np.arange(10),np.arange(2, 10, dtype=np.float),np.arange(2, 3, 0.1)
(array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9]),
array([2., 3., 4., 5., 6., 7., 8., 9.]),
array([2. , 2.1, 2.2, 2.3, 2.4, 2.5, 2.6, 2.7, 2.8, 2.9]))
linspace() 将创建具有指定数量元素的数组,并在指定的开始值和结束值之间平均间隔。例如:
np.linspace(1., 4., 6)
array([1. , 1.6, 2.2, 2.8, 3.4, 4. ])
这个创建函数的优点是可以保证元素的数量以及开始和结束点,对于任意的开始,停止和步骤值,arange()通常不会这样做。
indices() 将创建一组数组(堆积为一个更高维的数组),每个维度一个,每个维度表示该维度中的变化。一个例子说明比口头描述要好得多:
np.indices((3,3))
array([[[0, 0, 0],
[1, 1, 1],
[2, 2, 2]],
[[0, 1, 2],
[0, 1, 2],
[0, 1, 2]]])
从磁盘读取数组
这大概是大数组创建的最常见情况。当然,细节很大程度上取决于磁盘上的数据格式,所以本节只能给出如何处理各种格式的一般指示。
标准二进制格式
各种字段都有数组数据的标准格式。下面列出了那些已知的Python库来读取它们并返回numpy数组(可能有其他可能读取并转换为numpy数组的其他数据,因此请检查最后一节)
HDF5: h5py
FITS: Astropy
无法直接读取但不易转换的格式示例是像PIL这样的库支持的格式(能够读取和写入许多图像格式,如jpg,png等)。
常见ASCII格式
逗号分隔值文件(CSV)被广泛使用(以及Excel等程序的导出和导入选项)。有很多方法可以在Python中阅读这些文件。python中有CSV函数和pylab函数(matplotlib的一部分)。
更多通用的ascii文件可以在scipy中使用io软件包读取。
自定义二进制格式
有各种各样的方法可以使用。如果文件具有相对简单的格式,那么可以编写一个简单的 I/O 库,并使用 numpy fromfile() 函数和 .tofile() 方法直接读取和写入numpy数组(尽管介意你的字节序)!如果存在一个读取数据的良好 C 或 C++ 库,可以使用各种技术来封装该库,但这肯定要做得更多,并且需要更多的高级知识才能与C或C++ 接口。
使用特殊库
有些库可用于生成特殊用途的数组,且无法列出所有的这些库。最常见的用途是随机使用许多数组生成函数,这些函数可以生成随机值数组,以及一些实用函数来生成特殊矩阵(例如对角线)。
NumPy&Matplotlib
直线图
# 直线图
x = np.arange(1, 11)
y = 2 * x + 5
plt.title("demo")
plt.xlabel("x")
plt.ylabel("y")
plt.plot(x, y)
plt.show()
np.arange() 函数创建 x 轴上的值。y 轴上的对应值存储在另一个数组对象 y 中。 这些值使用 matplotlib 软件包的 pyplot 子模块的 plot() 函数绘制。
图形由 show() 函数显示。
作为线性图的替代,可以通过向 plot() 函数添加格式字符串来显示离散值。 可以使用以下格式化字符。
| 字符 | 描述 |
|---|---|
'-' |
实线样式 |
'--' |
短横线样式 |
'-.' |
点划线样式 |
':' |
虚线样式 |
'.' |
点标记 |
',' |
像素标记 |
'o' |
圆标记 |
'v' |
倒三角标记 |
'^' |
正三角标记 |
'<' |
左三角标记 |
'>' |
右三角标记 |
'1' |
下箭头标记 |
'2' |
上箭头标记 |
'3' |
左箭头标记 |
'4' |
右箭头标记 |
's' |
正方形标记 |
'p' |
五边形标记 |
'*' |
星形标记 |
'h' |
六边形标记 1 |
'H' |
六边形标记 2 |
'+' |
加号标记 |
'x' |
X 标记 |
'D' |
菱形标记 |
'd' |
窄菱形标记 |
'|' |
竖直线标记 |
'_' |
水平线标记 |
以下是颜色的缩写:
| 字符 | 颜色 |
|---|---|
'b' |
蓝色 |
'g' |
绿色 |
'r' |
红色 |
'c' |
青色 |
'm' |
品红色 |
'y' |
黄色 |
'k' |
黑色 |
'w' |
白色 |
import numpy as np
from matplotlib import pyplot as plt
x = np.arange(1,11)
y = 2 * x + 5
plt.title("Matplotlib demo")
plt.xlabel("x axis caption")
plt.ylabel("y axis caption")
plt.plot(x,y,"ob")
plt.show()
绘制正弦波
# 绘制正弦波
x = np.arange(0, 3 * np.pi, 0.1)
y = np.sin(x)
plt.title("sin(x)")
plt.plot(x, y, "--r")
plt.show()
subplot()
subplot() 函数允许你在同一图中绘制不同的东西。
有一点问题没有遇到过不知道该怎么解决,图片出现大量的乱序数字
# subplot()同一图中绘制不同的东西 ,
x = np.arange(0, 3 * np.pi, 0.1)
y_sin = np.sin(x)
y_cos = np.cos(x)
# 建立 subplot 网格,高为 2,宽为 1
# 激活第一个 subplot
plt.subplot(2, 1, 1)
# 绘制第一个图像
plt.plot(x, y_sin)
plt.title("sin(x)")
# 将第二个 subplot 激活,并绘制第二个图像
plt.subplot(2, 1, 2)
plt.plot(x, y_cos)
plt.title(np.cos(x))
# 展示图象
plt.show()
bar()
pyplot 子模块提供 bar() 函数来生成条形图。
以下实例生成两组 x 和 y 数组的条形图。
x = [5, 8, 10]
y = [12, 16, 6]
x2 = [6, 9, 11]
y2 = [6, 15, 7]
plt.bar(x, y, align='center')
plt.bar(x2, y2, color='g', align='center')
plt.title('Bar graph')
plt.ylabel('Y axis')
plt.xlabel('X axis')
plt.show()
numpy.histogram()
numpy.histogram() 函数是数据的频率分布的图形表示。 水平尺寸相等的矩形对应于类间隔,称为 bin,变量 height 对应于频率。
numpy.histogram()函数将输入数组和 bin 作为两个参数。 bin 数组中的连续元素用作每个 bin 的边界。
a = np.array([22, 87, 5, 43, 56, 73, 55, 54, 11, 20, 51, 5, 79, 31, 27])
np.histogram(a, bins=[0, 20, 40, 60, 80, 100])
hist, bins = np.histogram(a, bins=[0, 20, 40, 60, 80, 100])
print(hist)
print(bins)
[3 4 5 2 1]
[ 0 20 40 60 80 100]
plt()
Matplotlib 可以将直方图的数字表示转换为图形。 pyplot 子模块的 plt() 函数将包含数据和 bin 数组的数组作为参数,并转换为直方图。
a = np.array([22, 87, 5, 43, 56, 73, 55, 54, 11, 20, 51, 5, 79, 31, 27])
plt.hist(a, bins=[0, 20, 40, 60, 80, 100])
plt.title("histogram")
plt.show()