- Java 大视界 -- Java 大数据机器学习模型在金融市场情绪指数构建与投资决策支持中的应用(339)
青云交
大数据新视界Java大视界java大数据机器学习金融情绪指数投资决策量化策略情绪分析
Java大视界--Java大数据机器学习模型在金融市场情绪指数构建与投资决策支持中的应用(339)引言:正文:一、Java构建的金融市场情绪数据采集与预处理体系1.1多源异构数据接入引擎1.2数据采集延迟测试报告1.3情绪数据预处理管道二、Java驱动的金融市场情绪指数构建模型2.1多维度情绪指数计算框架2.2情绪指数与投资决策的映射模型三、Java在金融投资决策支持中的实战应用3.1量化私募情绪
- LangChain中的向量数据库接口-Weaviate
洪城叮当
langchain数据库经验分享笔记交互人工智能知识图谱
文章目录前言一、原型定义二、代码解析1、add_texts方法1.1、应用样例2、from_texts方法2.1、应用样例3、similarity_search方法3.1、应用样例三、项目应用1、安装依赖2、引入依赖3、创建对象4、添加数据5、查询数据总结前言 Weaviate是一个开源的向量数据库,支持存储来自各类机器学习模型的数据对象和向量嵌入,并能无缝扩展至数十亿数据对象。它提供存储文档嵌
- Python的科学计算库NumPy(一)
linlin_1998
pythonnumpy开发语言
NumPy(NumericalPython)是Python中最基础、最重要的科学计算库之一,提供了高性能的多维数组(ndarray)对象和大量数学函数,是许多数据科学、机器学习库(如Pandas、SciPy、TensorFlow等)的基础依赖。1.创建一个numpy里面的一维数组importnumpyasnp###通过array方法创建一个ndarrayarray1=np.array([1,2,3
- 微算法科技的前沿探索:量子机器学习算法在视觉任务中的革新应用
MicroTech2025
量子计算算法
在信息技术飞速发展的今天,计算机视觉作为人工智能领域的重要分支,正逐步渗透到我们生活的方方面面。从自动驾驶到人脸识别,从医疗影像分析到安防监控,计算机视觉技术展现了巨大的应用潜力。然而,随着视觉任务复杂度的不断提升,传统机器学习算法在处理大规模、高维度数据时遇到了计算瓶颈。在此背景下,量子计算作为一种颠覆性的计算模式,以其独特的并行处理能力和指数级增长的计算空间,为解决这一难题提供了新的思路。微算
- 在mac m1基于llama.cpp运行deepseek
lama.cpp是一个高效的机器学习推理库,目标是在各种硬件上实现LLM推断,保持最小设置和最先进性能。llama.cpp支持1.5位、2位、3位、4位、5位、6位和8位整数量化,通过ARMNEON、Accelerate和Metal支持Apple芯片,使得在MACM1处理器上运行Deepseek大模型成为可能。1下载llama.cppgitclonehttps://github.com/ggerg
- 【机器学习笔记Ⅰ】9 特征缩放
巴伦是只猫
机器学习机器学习笔记人工智能
特征缩放(FeatureScaling)详解特征缩放是机器学习数据预处理的关键步骤,旨在将不同特征的数值范围统一到相近的尺度,从而加速模型训练、提升性能并避免某些特征主导模型。1.为什么需要特征缩放?(1)问题背景量纲不一致:例如:特征1:年龄(范围0-100)特征2:收入(范围0-1,000,000)梯度下降的困境:量纲大的特征(如收入)会导致梯度更新方向偏离最优路径,收敛缓慢。量纲小的特征(如
- 深度学习实战-使用TensorFlow与Keras构建智能模型
程序员Gloria
Python超入门TensorFlowpython
深度学习实战-使用TensorFlow与Keras构建智能模型深度学习已经成为现代人工智能的重要组成部分,而Python则是实现深度学习的主要编程语言之一。本文将探讨如何使用TensorFlow和Keras构建深度学习模型,包括必要的代码实例和详细的解析。1.深度学习简介深度学习是机器学习的一个分支,使用多层神经网络来学习和表示数据中的复杂模式。其广泛应用于图像识别、自然语言处理、推荐系统等领域。
- 【大模型与机器学习解惑】什么是A/B测试,为何进行A/B测试?
以下内容将围绕机器学习中的A/B测试展开,从概念与背景到实施细节、示例代码、优化思路和未来建议,并在最后给出一个整体的“输出目录”供参考。目录什么是机器学习的A/B测试为何要进行A/B测试A/B测试的实施流程示例代码与详细解释优化方向与未来建议结语1.什么是机器学习的A/B测试A/B测试(也常被称作对照试验、SplitTest)最早多用于互联网产品的功能或界面迭代中,指的是将用户或样本随机分为两组
- 详解LLMOps,将DevOps用于大语言模型开发
大家好,在机器学习领域,随着技术的不断发展,将大型语言模型(LLMs)集成到商业产品中已成为一种趋势,同时也带来了许多挑战。为了有效应对这些挑战,数据科学家们转向了一种新型的DevOps实践LLM-OPS,专为大型语言模型的开发和维护而设计。本文将介绍LLM-OPS的核心思想,并分析这一策略如何帮助数据科学家更高效地运用DevOps的优秀实践,从而在语言模型的开发和部署过程中,提升工作效率和成果的
- 搜广推校招面经九十一
美团机器学习/数据挖掘算法工程师_二面一、介绍一下ESMM模型,是否有进行过函数推导传统的转化率建模方式:只用发生点击(click=1)的样本来训练CVR模型。CVR定义如下:CVR=P(y=1∣x,z=1)CVR=P(y=1|x,z=1)CVR=P(y=1∣x,z=1)y=1表示用户发生了转化(如购买)z=1表示用户点击了广告这样做的问题:样本选择偏差(SampleSelectionBias,S
- python 计算生态概览的概述
文章目录前言python计算生态库的介绍1.网络爬虫2.数据分析3.文本处理4.数据可视化5.机器学习6.图形用户界面7.游戏开发8.网络应用开发前言python计算生态概览的解释Python计算生态概览是对Python作为一门强大而广泛使用的编程语言所拥有的庞大软件集合的整体描述和概述。这个生态体系不仅包含了Python的标准库(stdlib),即随Python解释器安装的基本模块,还涵盖了极其
- Google机器学习实践指南(模型预测偏差)
AI_Auto
人工智能机器学习人工智能
Google机器学习(31)-模型预测偏差预测偏差:模型为何总是"猜不准"的真相揭秘你的模型预测准确率高达95%,却总是与实际情况差那么一点点?这可能是预测偏差在作祟!本文将带你深入探索这个被忽视的模型"隐形杀手"。一、什么是预测偏差?一个生活化案例想象一下,你网购了一个智能体重秤,连续一周称重显示都是60kg。但你去健身房用专业设备测量,实际是62kg。这种系统性的测量偏差,就是预测偏差在现实中
- 【机器学习|学习笔记】用 Python 结合 graphviz 生成 ID3、C4.5、CART 三种决策树的结构示意图。
【机器学习|学习笔记】用Python结合graphviz生成ID3、C4.5、CART三种决策树的结构示意图【机器学习|学习笔记】用Python结合graphviz生成ID3、C4.5、CART三种决策树的结构示意图文章目录【机器学习|学习笔记】用Python结合graphviz生成ID3、C4.5、CART三种决策树的结构示意图用Python结合graphviz生成ID3、C4.5、CART三种
- 智能产品经理的核心能力
AI天才研究院
AgenticAI实战AI人工智能与大数据AI大模型企业级应用开发实战计算科学神经计算深度学习神经网络大数据人工智能大型语言模型AIAGILLMJavaPython架构设计AgentRPA
智能产品经理的核心能力1.背景介绍在当今快节奏的数字时代,产品经理扮演着至关重要的角色,他们负责确保产品满足用户需求,实现商业目标,并保持竞争优势。随着人工智能(AI)和机器学习(ML)技术的不断发展,智能产品经理的概念应运而生。智能产品经理需要将传统的产品管理技能与新兴技术相结合,以创建具有创新性和智能化的产品体验。智能产品不仅需要满足功能需求,还需要提供个性化、智能化和无缝的用户体验。这对产品
- 使用Python进行机器学习入门指南
软考和人工智能学堂
Python开发经验python机器学习开发语言
使用Python进行机器学习入门指南机器学习(MachineLearning)是人工智能(ArtificialIntelligence,AI)的一个重要分支,旨在通过算法和统计模型,使计算机系统能够自动从数据中学习和改进。Python作为机器学习领域的主流编程语言,提供了丰富的库和工具来实现各种机器学习任务。本文将介绍如何使用Python进行机器学习,包括基本概念、常用库以及一个实战项目示例。目录
- 【亲测免费】 CatBoost 教程项目使用指南
CatBoost教程项目使用指南tutorials项目地址:https://gitcode.com/gh_mirrors/tutorials1/tutorials1.项目介绍CatBoost是一个高效、灵活且易于使用的梯度提升库,特别适用于处理分类特征。它由Yandex开发,广泛应用于机器学习和数据科学领域。CatBoost提供了丰富的功能,包括自动处理分类特征、支持GPU训练、内置的交叉验证和模
- Python自动化机器学习平台库之mindsdb使用详解
概要MindsDB是一个开源的自动化机器学习平台,它通过SQL接口简化了机器学习模型的创建、训练和预测过程。该库的核心理念是将机器学习功能直接集成到数据库中,让开发者无需深入了解复杂的机器学习算法,就能够快速构建和部署预测模型。MindsDB支持多种数据源连接,包括MySQL、PostgreSQL、MongoDB等主流数据库,同时提供了丰富的PythonAPI接口,使得数据科学家和开发者能够在熟悉
- 堡垒机操作行为异常检测的机器学习算法应用
一、传统检测模式的困境与机器学习的破局价值在数字化转型浪潮中,堡垒机作为运维安全的核心防线,面临着操作行为复杂度激增与检测能力滞后的双重挑战。传统检测手段主要依赖静态规则库与统计模型,存在三大致命缺陷:规则固化与误报泛滥:某金融机构曾因规则库未及时更新,导致运维人员正常批量操作被误判为“暴力破解”,单日误报量超2000次,消耗安全团队60%的精力。动态行为适应性弱:微服务架构下,运维人员访问路径呈
- 最全 自动驾驶数据集 (11/4号已更新)
数据猎手小k
自动驾驶人工智能机器学习
自动驾驶是一个快速发展的行业,它融合了人工智能、机器学习、传感器技术、高精度地图和先进的计算平台等多种技术。技术方面,自动驾驶汽车依赖于先进的传感器、如激光雷达、摄像头、毫米波雷达等,以及强大的计算平台来处理大量数据,自动驾驶数据集是训练和验证自动驾驶系统的关键资源,它提供了丰富的场景和条件,使算法能够学习和适应复杂的真实世界驾驶环境。一、研究背景自动驾驶技术的发展需要大量的数据来训练和优化算法,
- 机器学习深度学习驱动在光子学设计中的应用与未来【专题培训会议邀您共探科技前沿】
软研科技
信息与通信信号处理量子计算人工智能
一、背景介绍在智能科技飞速发展的今天,光子学设计与智能算法的结合正成为科研创新的热点。深度学习、机器学习等算法在光子器件的逆向设计、超构表面材料设计、光学神经网络构建等方面展现出巨大潜力。二、会议亮点由北京软研国际信息技术研究院主办的“智能算法驱动的光子学设计与应用”专题培训会议,将深入探讨以下核心内容:光子器件的逆向设计:利用深度学习优化多参数光子器件设计。超构表面与超材料设计:智能算法在新型光
- 机器学习与光子学的融合正重塑光学器件设计范式
m0_75133639
光电智能电视二维材料电子半导体人工智能顶刊nature
Nature/Science最新研究表明,该交叉领域聚焦六大前沿方向:光子器件逆向设计、超构材料智能优化、光子神经网络加速器、非线性光学芯片开发、多任务协同优化及光谱智能预测。系统掌握该领域需构建四维知识体系:1、基础融合——从空间/集成光学系统切入,解析机器学习赋能光学的理论必然性,涵盖光学神经网络构建原理2、逆向设计革命——通过AnsysOptics实战,掌握FDTD算法与粒子群/拓扑优化技术
- AI模型训练新范式:基于同态加密的隐私保护方案
AIGC应用创新大全
人工智能同态加密区块链ai
AI模型训练新范式:基于同态加密的隐私保护方案技术解析关键词同态加密(HomomorphicEncryption)、隐私保护机器学习(PPML)、全同态加密(FHE)、安全多方计算(MPC)、加密数据训练摘要本报告系统解析基于同态加密的AI模型训练新范式,覆盖从理论基础到工程实践的全生命周期。首先通过第一性原理推导同态加密的数学本质,对比传统隐私保护技术的局限性;其次构建“加密-训练-解密”全流程
- 量子机器学习入门:从理论到实践
量子机器学习入门:从理论基石到实践路径元数据框架标题量子机器学习入门:从理论基石到实践路径——连接量子计算与人工智能的未来桥梁关键词量子计算;机器学习;量子算法;量子神经网络;Qiskit;PennyLane;量子变分算法摘要量子机器学习(QuantumMachineLearning,QML)是量子计算与机器学习的交叉领域,通过量子计算的叠加态、纠缠和并行性解决传统机器学习的计算瓶颈(如高维数据处
- 全球人工智能与机器学习大会PPT
a flying bird
论文解读和大咖技术号记录人工智能
大会演讲PPT合集https://ppt.infoq.cn/list/93PPT分享|ppt|人工智能|aicon|infoq|机器学习PPT分享,前段时间的AICon北京站2021全球人工智能与机器学习大会(https://aicon.infoq.cn/2021/beijing),汇集了很多业界大佬,工业界多个方向的从业人员分享了他们在实际业……https://xw.qq.com/cmsid/2
- 人工智能基础知识PPT课件
智慧化智能化数字化方案
方案解读馆人工智能入门人工智能学习人工智能课件人工智能PPT
人工智能基础知识定义与概念:人工智能是研究、开发用于模拟、延伸和扩展人类智能行为的综合性科学,其目的是让计算机系统具备执行人类智能任务的能力。涉及计算机科学、数学等多学科,研究对象是让系统具备智能,智能包括认知、适应和自主能力等维度。学派与方法学派:有符号主义、联结主义、行为主义等学派,分别从不同角度研究人工智能。方法:包括基于知识、学习和仿生的方法,如专家系统、机器学习、深度学习等。分类与发展分
- 数据挖掘:从理论到实践的深度探索
代码老y
数据挖掘人工智能
在当今数字化时代,数据已经成为企业决策的重要依据。数据挖掘作为一门从大量数据中提取有价值信息的技术,已经广泛应用于各个领域,如金融、医疗、零售、互联网等。本文将深入探讨数据挖掘的基本概念、主要技术和实际应用案例,帮助读者更好地理解数据挖掘的价值和应用。一、数据挖掘的基本概念(一)数据挖掘的定义数据挖掘(DataMining)是从大量数据中提取有用信息的过程。它结合了统计学、机器学习、数据库技术和人
- 开发智能化的企业并购风险评估模型
开发智能化的企业并购风险评估模型关键词:企业并购、风险评估、人工智能、机器学习、深度学习、数学建模摘要:本文详细探讨了开发智能化企业并购风险评估模型的背景、核心概念、算法原理、系统架构设计以及项目实战。通过结合机器学习和深度学习技术,提出了一种基于数据驱动的智能化风险评估方法,旨在帮助企业更准确地识别和预测并购过程中的潜在风险,提升决策的科学性和有效性。第1章:企业并购风险评估模型的背景与问题描述
- 机器学习手写字体识别系统:技术演进与应用实践
万能小贤哥
机器学习人工智能
引言:手写字体识别的技术定位与价值在信息处理领域,人工录入手写文本的低效性与机器识别的高效性形成鲜明对比。例如,医疗处方的人工处理需约5分钟/张,而采用手写字体识别技术可将时间缩短至10秒/张,显著提升处理效率。作为计算机视觉与人工智能的重要分支,手写字体识别技术通过将手写文本转换为可编辑电子文本,不仅大幅减少人工输入时间和错误,降低人工处理成本,还能在大量数据处理时保持高于人工录入的准确性,是人
- 机器学习算法:核心原理与前沿发展综述
fmvrj34202
机器学习算法人工智能
机器学习算法作为人工智能的核心驱动力,正在重塑我们解决问题的范式。本文将系统性地探讨机器学习算法的分类体系、数学基础、优化方法以及最新发展趋势,为从业者提供技术参考。一、算法分类体系根据学习范式,机器学习算法可分为三大类:监督学习:基于标注数据的建模方法线性回归:最小化平方误差的闭式解θ=(XᵀX)⁻¹Xᵀy支持向量机:通过核技巧实现非线性分类,优化目标为max(0,1-yᵢ(w·xᵢ+b))决策
- 「日拱一码」020 机器学习——数据处理
胖达不服输
「日拱一码」机器学习人工智能数据处理python
目录数据清洗缺失值处理删除缺失值:填充缺失值:重复值处理检测重复值处理重复值异常值处理Z-score方法IQR方法(四分位距)数据一致性检查数据转换规范化(归一化)Min-Max归一化MaxAbsScaler标准化离散化等宽离散化等频离散化数据清洗数据清洗是数据处理的第一步,目的是去除噪声数据、处理缺失值和异常值,使数据更加干净、可用缺失值处理删除缺失值:如果数据集中缺失值较少,可以直接删除包含缺
- 对于规范和实现,你会混淆吗?
yangshangchuan
HotSpot
昨晚和朋友聊天,喝了点咖啡,由于我经常喝茶,很长时间没喝咖啡了,所以失眠了,于是起床读JVM规范,读完后在朋友圈发了一条信息:
JVM Run-Time Data Areas:The Java Virtual Machine defines various run-time data areas that are used during execution of a program. So
- android 网络
百合不是茶
网络
android的网络编程和java的一样没什么好分析的都是一些死的照着写就可以了,所以记录下来 方便查找 , 服务器使用的是TomCat
服务器代码; servlet的使用需要在xml中注册
package servlet;
import java.io.IOException;
import java.util.Arr
- [读书笔记]读法拉第传
comsci
读书笔记
1831年的时候,一年可以赚到1000英镑的人..应该很少的...
要成为一个科学家,没有足够的资金支持,很多实验都无法完成
但是当钱赚够了以后....就不能够一直在商业和市场中徘徊......
- 随机数的产生
沐刃青蛟
随机数
c++中阐述随机数的方法有两种:
一是产生假随机数(不管操作多少次,所产生的数都不会改变)
这类随机数是使用了默认的种子值产生的,所以每次都是一样的。
//默认种子
for (int i = 0; i < 5; i++)
{
cout<<
- PHP检测函数所在的文件名
IT独行者
PHP函数
很简单的功能,用到PHP中的反射机制,具体使用的是ReflectionFunction类,可以获取指定函数所在PHP脚本中的具体位置。 创建引用脚本。
代码:
[php]
view plain
copy
// Filename: functions.php
<?php&nbs
- 银行各系统功能简介
文强chu
金融
银行各系统功能简介 业务系统 核心业务系统 业务功能包括:总账管理、卡系统管理、客户信息管理、额度控管、存款、贷款、资金业务、国际结算、支付结算、对外接口等 清分清算系统 以清算日期为准,将账务类交易、非账务类交易的手续费、代理费、网络服务费等相关费用,按费用类型计算应收、应付金额,经过清算人员确认后上送核心系统完成结算的过程 国际结算系
- Python学习1(pip django 安装以及第一个project)
小桔子
pythondjangopip
最近开始学习python,要安装个pip的工具。听说这个工具很强大,安装了它,在安装第三方工具的话so easy!然后也下载了,按照别人给的教程开始安装,奶奶的怎么也安装不上!
第一步:官方下载pip-1.5.6.tar.gz, https://pypi.python.org/pypi/pip easy!
第二部:解压这个压缩文件,会看到一个setup.p
- php 数组
aichenglong
PHP排序数组循环多维数组
1 php中的创建数组
$product = array('tires','oil','spark');//array()实际上是语言结构而不 是函数
2 如果需要创建一个升序的排列的数字保存在一个数组中,可以使用range()函数来自动创建数组
$numbers=range(1,10)//1 2 3 4 5 6 7 8 9 10
$numbers=range(1,10,
- 安装python2.7
AILIKES
python
安装python2.7
1、下载可从 http://www.python.org/进行下载#wget https://www.python.org/ftp/python/2.7.10/Python-2.7.10.tgz
2、复制解压
#mkdir -p /opt/usr/python
#cp /opt/soft/Python-2
- java异常的处理探讨
百合不是茶
JAVA异常
//java异常
/*
1,了解java 中的异常处理机制,有三种操作
a,声明异常
b,抛出异常
c,捕获异常
2,学会使用try-catch-finally来处理异常
3,学会如何声明异常和抛出异常
4,学会创建自己的异常
*/
//2,学会使用try-catch-finally来处理异常
- getElementsByName实例
bijian1013
element
实例1:
<!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Transitional//EN" "http://www.w3.org/TR/xhtml1/DTD/xhtml1-transitional.dtd">
<html xmlns="http://www.w3.org/1999/x
- 探索JUnit4扩展:Runner
bijian1013
java单元测试JUnit
参加敏捷培训时,教练提到Junit4的Runner和Rule,于是特上网查一下,发现很多都讲的太理论,或者是举的例子实在是太牵强。多搜索了几下,搜索到两篇我觉得写的非常好的文章。
文章地址:http://www.blogjava.net/jiangshachina/archive/20
- [MongoDB学习笔记二]MongoDB副本集
bit1129
mongodb
1. 副本集的特性
1)一台主服务器(Primary),多台从服务器(Secondary)
2)Primary挂了之后,从服务器自动完成从它们之中选举一台服务器作为主服务器,继续工作,这就解决了单点故障,因此,在这种情况下,MongoDB集群能够继续工作
3)挂了的主服务器恢复到集群中只能以Secondary服务器的角色加入进来
2
- 【Spark八十一】Hive in the spark assembly
bit1129
assembly
Spark SQL supports most commonly used features of HiveQL. However, different HiveQL statements are executed in different manners:
1. DDL statements (e.g. CREATE TABLE, DROP TABLE, etc.)
- Nginx问题定位之监控进程异常退出
ronin47
nginx在运行过程中是否稳定,是否有异常退出过?这里总结几项平时会用到的小技巧。
1. 在error.log中查看是否有signal项,如果有,看看signal是多少。
比如,这是一个异常退出的情况:
$grep signal error.log
2012/12/24 16:39:56 [alert] 13661#0: worker process 13666 exited on s
- No grammar constraints (DTD or XML schema).....两种解决方法
byalias
xml
方法一:常用方法 关闭XML验证
工具栏:windows => preferences => xml => xml files => validation => Indicate when no grammar is specified:选择Ignore即可。
方法二:(个人推荐)
添加 内容如下
<?xml version=
- Netty源码学习-DefaultChannelPipeline
bylijinnan
netty
package com.ljn.channel;
/**
* ChannelPipeline采用的是Intercepting Filter 模式
* 但由于用到两个双向链表和内部类,这个模式看起来不是那么明显,需要仔细查看调用过程才发现
*
* 下面对ChannelPipeline作一个模拟,只模拟关键代码:
*/
public class Pipeline {
- MYSQL数据库常用备份及恢复语句
chicony
mysql
备份MySQL数据库的命令,可以加选不同的参数选项来实现不同格式的要求。
mysqldump -h主机 -u用户名 -p密码 数据库名 > 文件
备份MySQL数据库为带删除表的格式,能够让该备份覆盖已有数据库而不需要手动删除原有数据库。
mysqldump -–add-drop-table -uusername -ppassword databasename > ba
- 小白谈谈云计算--基于Google三大论文
CrazyMizzz
Google云计算GFS
之前在没有接触到云计算之前,只是对云计算有一点点模糊的概念,觉得这是一个很高大上的东西,似乎离我们大一的还很远。后来有机会上了一节云计算的普及课程吧,并且在之前的一周里拜读了谷歌三大论文。不敢说理解,至少囫囵吞枣啃下了一大堆看不明白的理论。现在就简单聊聊我对于云计算的了解。
我先说说GFS
&n
- hadoop 平衡空间设置方法
daizj
hadoopbalancer
在hdfs-site.xml中增加设置balance的带宽,默认只有1M:
<property>
<name>dfs.balance.bandwidthPerSec</name>
<value>10485760</value>
<description&g
- Eclipse程序员要掌握的常用快捷键
dcj3sjt126com
编程
判断一个人的编程水平,就看他用键盘多,还是鼠标多。用键盘一是为了输入代码(当然了,也包括注释),再有就是熟练使用快捷键。 曾有人在豆瓣评
《卓有成效的程序员》:“人有多大懒,才有多大闲”。之前我整理了一个
程序员图书列表,目的也就是通过读书,让程序员变懒。 程序员作为特殊的群体,有的人可以这么懒,懒到事情都交给机器去做,而有的人又可以那么勤奋,每天都孜孜不倦得
- Android学习之路
dcj3sjt126com
Android学习
转自:http://blog.csdn.net/ryantang03/article/details/6901459
以前有J2EE基础,接触JAVA也有两三年的时间了,上手Android并不困难,思维上稍微转变一下就可以很快适应。以前做的都是WEB项目,现今体验移动终端项目,让我越来越觉得移动互联网应用是未来的主宰。
下面说说我学习Android的感受,我学Android首先是看MARS的视
- java 遍历Map的四种方法
eksliang
javaHashMapjava 遍历Map的四种方法
转载请出自出处:
http://eksliang.iteye.com/blog/2059996
package com.ickes;
import java.util.HashMap;
import java.util.Iterator;
import java.util.Map;
import java.util.Map.Entry;
/**
* 遍历Map的四种方式
- 【精典】数据库相关相关
gengzg
数据库
package C3P0;
import java.sql.Connection;
import java.sql.SQLException;
import java.beans.PropertyVetoException;
import com.mchange.v2.c3p0.ComboPooledDataSource;
public class DBPool{
- 自动补全
huyana_town
自动补全
<!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Transitional//EN" "http://www.w3.org/TR/xhtml1/DTD/xhtml1-transitional.dtd"><html xmlns="http://www.w3.org/1999/xhtml&quo
- jquery在线预览PDF文件,打开PDF文件
天梯梦
jquery
最主要的是使用到了一个jquery的插件jquery.media.js,使用这个插件就很容易实现了。
核心代码
<!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Transitional//EN" "http://www.w3.org/TR/xhtml1/DTD/xhtml1-transitional.
- ViewPager刷新单个页面的方法
lovelease
androidviewpagertag刷新
使用ViewPager做滑动切换图片的效果时,如果图片是从网络下载的,那么再子线程中下载完图片时我们会使用handler通知UI线程,然后UI线程就可以调用mViewPager.getAdapter().notifyDataSetChanged()进行页面的刷新,但是viewpager不同于listview,你会发现单纯的调用notifyDataSetChanged()并不能刷新页面
- 利用按位取反(~)从复合枚举值里清除枚举值
草料场
enum
以 C# 中的 System.Drawing.FontStyle 为例。
如果需要同时有多种效果,
如:“粗体”和“下划线”的效果,可以用按位或(|)
FontStyle style = FontStyle.Bold | FontStyle.Underline;
如果需要去除 style 里的某一种效果,
- Linux系统新手学习的11点建议
刘星宇
编程工作linux脚本
随着Linux应用的扩展许多朋友开始接触Linux,根据学习Windwos的经验往往有一些茫然的感觉:不知从何处开始学起。这里介绍学习Linux的一些建议。
一、从基础开始:常常有些朋友在Linux论坛问一些问题,不过,其中大多数的问题都是很基础的。例如:为什么我使用一个命令的时候,系统告诉我找不到该目录,我要如何限制使用者的权限等问题,这些问题其实都不是很难的,只要了解了 Linu
- hibernate dao层应用之HibernateDaoSupport二次封装
wangzhezichuan
DAOHibernate
/**
* <p>方法描述:sql语句查询 返回List<Class> </p>
* <p>方法备注: Class 只能是自定义类 </p>
* @param calzz
* @param sql
* @return
* <p>创建人:王川</p>
* <p>创建时间:Jul
![]() 是指在train的过程中output的y与实际的y之间的距离Function(类似cross entropy),这个距离越小表示output的结果越好。
是指在train的过程中output的y与实际的y之间的距离Function(类似cross entropy),这个距离越小表示output的结果越好。![]() )则是所有样本数据的距离之和,以此作为Loss Function。
)则是所有样本数据的距离之和,以此作为Loss Function。![]() )对于参数w的微分转换成另外一种形式。
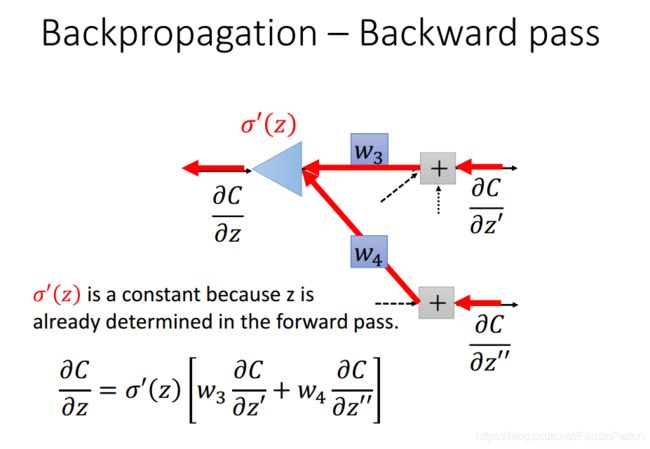
)对于参数w的微分转换成另外一种形式。![]() 进一步转换,并将转换后的微分分为Forward pass和Backward pass。
进一步转换,并将转换后的微分分为Forward pass和Backward pass。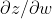 的方法
的方法![]() 其实就是输入的x
其实就是输入的x![]() ,这部分才是体现出反向传播的精髓。
,这部分才是体现出反向传播的精髓。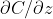
![]()
![]() ,下面就根据chain rule计算
,下面就根据chain rule计算![]()
![]() 与求下一层neural network的输入z有关.
与求下一层neural network的输入z有关.![]() 的直观的流程图,体现了“反向”
的直观的流程图,体现了“反向”![]()