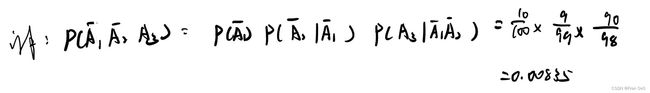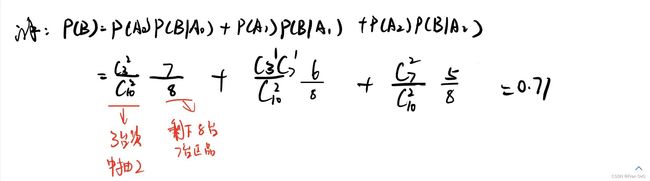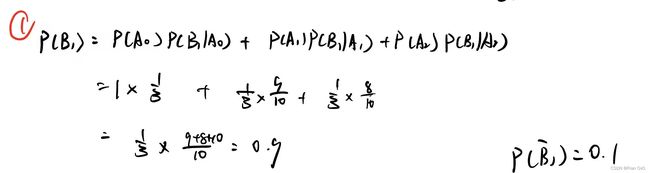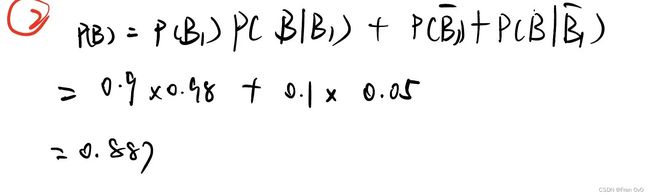分类模型（2）——朴素贝叶斯

        朴素贝叶斯（Naive Bayes）是经典的机器学习算法之一，是基于概率论的分类算法。

        在机器学习分类算法中，朴素贝叶斯和其他绝大多数的分类算法都不同。比如决策树，KNN，逻辑回归，支持向量机等，他们都是判别方法，也就是直接学习出特征输出Y和特征X之间的关系，要么是决策函数，要么是条件分布。但是朴素贝叶斯却是生成方法。

目录

一、概率论

条件概率

 乘法公式eg1：

全概率公式

 全概率eg1:

 全概率eg2：

贝叶斯公式

 贝叶斯eg1：

 贝叶斯eg2：

二、机器学习朴素贝叶斯

1，算法的原理

 2，好瓜坏瓜数据集实验

---

一、概率论

回忆一波亘古的知识……

先验概率：即基于统计的概率，是基于以往历史经验和分析得到的结果，不需要依赖当前发生的条件。

后验概率：则是从条件概率而来，由因推果，是基于当下发生了事件之后计算的概率，依赖于当前发生的条件。

条件概率

记事件A发生的概率为P(A)，事件B发生的概率为P(B)，则在B事件发生的前提下，A事件发生的概率即为条件概率，记为P(A|B)。

                                                        

乘法公式：

 乘法公式eg1：

共有产品100件，次品率为10%（合格率为90%），随机抽，不放回，第三次才取到合格品的概率：

假设设取第一，二，三次为合格品的事件为

全概率公式

表示若事件构成一个完备事件组（互不相容），则对任意一个事件B都有公式成立：                             

                                                         

 全概率eg1:

10台机器，3台次品（7台正品）已售2台，再取一台是正品的概率

假设：事件是第三次为正品，事件为前两台都是次品，事件:一次品一正品，事件:都是正品

 全概率eg2：

10件产品，次品可能数量为0，1，2件，正品被检验成正品的概率为0.98，被检验成次品的概率为0.02。

次品被检验成正品的概率为0.05，被检验成次品的概率为0.95

求产品通过检验的可能性：

假设:通过验证

事件为次品数量为0，1，2件

事件为抽的是正品

则可以得到   , 

次品数量为0的情况下抽中正品的概率为 

次品数量为1的情况下抽中正品的概率为 （抽了9件正品）

次品数量为2的情况下抽中正品的概率为 （抽了8件正品）

抽中正品的概率为：

 

 那么通过检验的概率就可以为抽中正品过了和抽中次品过了的全概率

贝叶斯公式

贝叶斯公式便是基于条件概率，通过P(B|A)来求P(A|B)，如下：

                                                        
 

将全概率公式带入贝叶斯公式中，得到：

                                                                  

这就是一个由结果推原因的过程

                               

 贝叶斯eg1：

四条生产线进行抽查，其中第一生产线抽中的概率为15%，不合格率为0.05，第二生产线抽中的概率为20%，不合格率为0.04，第三生产线抽中的概率为30%，不合格率为0.03，第四生产线抽中的概率为35%，不合格率为0.02。

现在抽一批最终产品，结果抽到了个次品，求整出这个次品概率最大的生产线：

假设事件为抽中第一，二，三，四生产线，B事件为产品不合格

可以写成全概率：

这时候就可以利用乘法公式：

 贝叶斯eg2：

某个地区有一种病，发病率为0.0004  ，患者去医院被判确诊的概率为99%，误判的概率为1%

健康人去医院检测无病的概率为99.9%，误判确诊的概率为0.1%

 求该医院检测确诊且正确的概率：

假设事件为患者，为健康者 ,事件B为确诊的

患者，健康

患者去医院被确诊

健康者去医院被确诊的

计算出确诊的全概率：

 则确诊且正确的概率为：

二、机器学习朴素贝叶斯

1，算法的原理

特征条件假设：假设每个特征之间没有联系，给定训练数据集，其中每个样本都包括维特征，即，类标记集合含有种类别，即。

对于给定的新样本，判断其属于哪个标记的类别，根据贝叶斯定理，可以得到属于类别的概率：

                                                        

后验概率最大的类别记为预测类别：

朴素贝叶斯算法对条件概率分布作出了独立性的假设，通俗地讲就是说假设各个维度的特征互相独立，在这个假设的前提上，条件概率可以转化为：

                                        

代入贝叶斯公式：

                                ​​​​​​​        ​​​​​​​        

于是，朴素贝叶斯分类器可表示为：

                                  

因为对所有的，上式中的分母的值都是一样的，所以可以忽略分母部分，朴素贝叶斯分类器最终表示为：

        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​·        

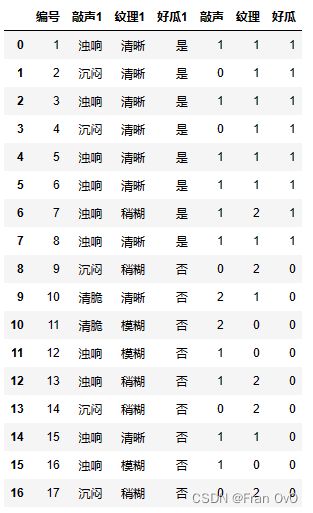
 2，好瓜坏瓜数据集实验

 1，贝叶斯计算

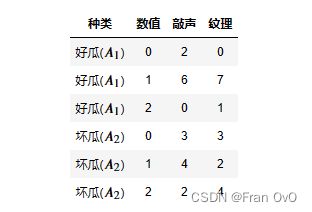
统计：好瓜和坏瓜中，敲声为0/1/2（沉闷/浊响/清脆）的频次，以及纹理为0/1/2（模糊/清晰/稍糊）的频次。

假设对某个瓜进行了测量，测得"敲声为1，纹理为2"，视此为事件B。

可得： ，

1）求：在好瓜A1的前提下，敲声为1的概率是多少？纹理为2的概率是多少？“敲声为1且纹理为2”的概率是多少？

假设：事件C1为敲声为1，事件C2为纹理为2

    ,     

则

2）求：在坏瓜的前提下，敲声为1的概率是多少？纹理为2的概率是多少？“敲声为1且纹理为2”的概率是多少？

假设：事件C1为敲声为1，事件C2为纹理为2

    ,     

则

3）求测得“敲声为1，纹理为2”的前提下，它是好瓜的概率是多少？

2，sklearn代码训练

import pandas as pd
filename = '/data/bigfiles/watermelon.csv'
watermelon = pd.read_csv(filename)
watermelon
X, y = watermelon[['敲声','纹理']], watermelon['好瓜']

from sklearn.naive_bayes import BernoulliNB
model = BernoulliNB()
model.fit(X,y)
s = model.score(X, y)
s

利用 GaussianNB进行分类可以提高准确性

from sklearn.naive_bayes import GaussianNB
model_Gas = GaussianNB()
model_Gas.fit(X,y)
s = model_Gas.score(X, y)
s