数理统计——朴素贝叶斯分类

前言

1. 熟悉条件概率、联合概率、独立性概率
2. 熟悉全概率公式与贝叶斯公式
3. 清楚朴素贝叶斯算法原理
4. 能使用该算法实现分类任务

一、重要概念

朴素贝叶斯算法：
核心思维：是基于概率的算法，之所以称为朴素，是因为其假设特征之间是独立的，该算法设计比较简单，实际上使用的是全概率公式和贝叶斯公式。朴素贝叶斯在文本场景中效果非常好，例如垃圾邮件过滤，新闻分类，情感分析。

1. 正向概率：站在上帝视角，即了解事情的全貌再做判断。例如预先知道袋子里有n个球，白球有m个，黑球有b个，所以能知道知道伸手进去拿到黑球的概率是多少。也叫先验概率，是指通过经验来判断事情发生的概率。
2. 负向概率：相对于正向概率而言。从在实际场景出发，在不了解所有客观事实的基础上，先估计一个值，然后根据实际结果进行不断修正。也叫后验概率，是指发生结果之后，推测原因的概率。比如某人患有“贝叶死病”，患病的原因可能有A,B,C,推测患有“贝叶死”是因为原因A的概率就是后验概率，它是属于条件概率的一种。
3. 条件概率：是指事件A在另外一个事件B已经发生的条件下A发生的概率，表示为P(A|B），读作在B发生的条件下A发生的概率。
4. 似然函数：用来衡量模型的参数，是关于统计函数的参数。
5. 贝叶斯原理：就是求解后验概率。贝叶斯公式：其核心思维是将求解p(A|B)的概率转换成求解p(B|A)的概率，因为有时求解p(A|B)的难度较大，但是求解p(B|A)的难度较小。

通过一个例子来说明：
还有嫁和不嫁的例子。
下面是通用的贝叶斯公式：

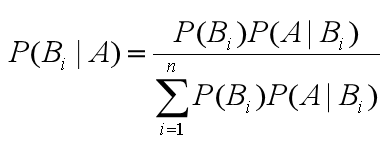
6、朴素贝叶斯：是一种极为简单但较为强大的预测建模算法，之所以称为朴素，是因为它假设每个变量是独立的。

朴素贝叶斯模型由两种类型的概率组成：

• 每个类别的概率P（Bi）
• 每个属性的条件概率P(A|Bi)

7、什么是类别概率：有7个棋子，3个是白色，4个是黑色，那么3/7和4/7的白色和黑色概率就是类别概率。
8、什么是条件概率：把棋子放进A,B盒子里，A盒子里放2个白旗、2个黑旗，B盒子放1个白旗、2个黑旗，那么在盒子A中抓到白色棋子的概率就是1/2，这个就是条件概率，也就是在某个条件下的概率。
在朴素贝叶斯中，我们要求的就是属性的条件概率，也就是假设取出来的是白色的棋子，它属于A盒子的概率是2/3。
9、区分贝叶斯原理、贝叶斯分类、朴素贝叶斯
10、全概率公式

二.朴素贝叶斯分类器工作流程

先验概率：以经验进行判断；
后验概率：以结果进行判断；
条件概率：在某种条件下，发生结果的概率。

对于离散变量可以直接求概率，连续变量需要看正态分布，然后计算期望和标准差 ，来计算概率。

三、如何使用朴素贝叶斯分类对文档进行分类

朴素贝叶斯适用场景：

• 文本分类
• 情感分析
• 垃圾邮件识别

sklearn机器学习包： 提供了3个朴素贝叶斯分类算法：

1. 高斯朴素贝叶斯：连续变量,且符合正态分布的情况。比如身高、长度

高斯朴素贝叶斯
from sklearn.naive_bayes import GaussianNB
import numpy as np 
import pandas as pd 
np.random.seed(0)
x=np.random.randint(0,10,size=(6,2))
y=np.array([0,0,0,1,1,1])
data=pd.DataFrame(np.concatenate([x,y.reshape(-1,1)],axis=1),columns=["x1","x2","y"])
display(data)

gnb=GaussianNB()
gnb.fit(x,y)
#每个类别的先验概率
print("概率：",gnb.class_prior_)
#每个类别样本的数量
print("样本数量：",gnb.class_count_)
#每个类别的标签
print("标签：",gnb.classes_)
#每个特征在每个类别下的均值
print("均值：",gnb.theta_)
#每个特征在每个类别下的方差
print("方差：",gnb.sigma_)

#测试集
x_test=np.array([[6,3]])
print("预测结果：",gnb.predict(x_test))
print("预测结果概率：",gnb.predict_proba(x_test))

输出：
	x1	x2	y
0	5	0	0
1	3	3	0
2	7	9	0
3	3	5	1
4	2	4	1
5	7	6	1
概率： [0.5 0.5]
样本数量： [3. 3.]
标签： [0 1]
均值： [[5. 4.]
 [4. 5.]]
方差： [[ 2.66666667 14.00000001]
 [ 4.66666667  0.66666667]]
预测结果： [0]
预测结果概率： [[0.87684687 0.12315313]]

3. 伯努利朴素贝叶斯：离散变量，特征变量是布尔变量，符合0/1分布，在文档分类中体现为单词是否出现。以文件为粒度，如果在文件中出现即为1，否则为0。

 #使用伯努利朴素贝叶斯\
from sklearn.naive_bayes import BernoulliNB
np.random.seed(0)
x=np.random.randint(-5,5,size=(6,2))
y=np.array([0,0,0,1,1,1])
data=pd.DataFrame(np.concatenate([x,y.reshape(-1,1)],axis=1),columns=["x1","x2","y"]) 
display(data)
bnb=BernoulliNB()
bnb.fit(x,y)
print("数值1出现次数：",bnb.feature_count_)
print("类别占比p(y):",np.exp(bnb.class_log_prior_))
print("特征概率：",np.exp(bnb.feature_log_prob_))

输出：
	x1	x2	y
0	0	-5	0
1	-2	-2	0
2	2	4	0
3	-2	0	1
4	-3	-1	1
5	2	1	1
数值1出现次数： [[1. 1.]
 [1. 1.]]
类别占比p(y): [0.5 0.5]
特征概率： [[0.4 0.4]
 [0.4 0.4]]

5. 多项式朴素贝叶斯：适用于离散变量，比如文档分类中单词出现频数，或者单词的TF-IDF值。以单词为粒度，会计算在某个文件中的具体次数。

from sklearn.naive_bayes import MultinomialNB

np.random.seed(0)
X = np.random.randint(0, 4, size=(6, 2))
y = np.array([0, 0, 0, 1, 1, 1])
data = pd.DataFrame(np.concatenate([X, y.reshape(-1, 1)], axis=1), columns=["x1", "x2", "y"]) 
display(data)

mnb = MultinomialNB() 
mnb.fit(X, y)
# 每个类别的样本数量。
print(mnb.class_count_)
# 每个特征在每个类别下发生(出现)的次数。 
print(mnb.feature_count_)
# 每个类别下，每个特征所占的比例(概率)，即P(x}y)。注意，该值为概率 
# 取对数之后的结果，如果需要查看原有的概率，需要使用指数还原。 
print(np.exp(mnb.feature_log_prob_))
输出：
	x1	x2	y
0	0	3	0
1	1	0	0
2	3	3	0
3	3	3	1
4	1	3	1
5	1	2	1
[3. 3.]
[[4. 6.]
 [5. 8.]]
[[0.41666667 0.58333333]
 [0.4        0.6       ]]

对于鸢尾花数据集进行分类，那种算法更好？

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split 
x,y=load_iris(return_X_y=True)
x_train,x_test,y_train,y_test=train_test_split(x,y,test_size=0.25,random_state=0)
models=[("多项式朴素贝叶斯：",MultinomialNB()),("高斯朴素贝叶斯:",GaussianNB()),("伯努利朴素贝叶斯:",BernoulliNB())]
for name,m in models:
    m.fit(x_train,y_train)
    print(name,m.score(x_test,y_test))

输出：
多项式朴素贝叶斯： 0.5789473684210527
高斯朴素贝叶斯: 1.0
伯努利朴素贝叶斯: 0.23684210526315788

什么是TF-IDF值？

• 是一个统计方法，用来评估某一个词语对于一个文件集或文档库中的其中一份文件的重要程度。TF-IDF 实际上是两个词组 Term Frequency 和 Inverse Document Frequency 的乘积，两者缩写为 TF 和 IDF，分别代表了词频和逆向文档频率。
• 词频 TF 计算了一个单词在文档中出现的次数，它认为一个单词的重要性和它在文档中出现的次数呈正比。
• 逆向文档频率 IDF，是指一个单词在文档中的区分度。它认为一个单词出现在的文档数越少，就越能通过这个单词把该文档和其他文档区分开。IDF 越大就代表该单词的区分度越大。

TF-IDF值如何计算？


TF-IDF=TF*IDF
举个例子:假设一个文件夹里一共有 10 篇文档，其中一篇文档有 1000 个单词，“this”这个单词出现 20 次，“bayes”出现了 5 次。“this”在所有文档中均出现过，而“bayes”只在 2 篇文档中出现过。我们来计算一下这两个词语的 TF-IDF 值。
针对“this”，计算 TF-IDF 值：

词频TF=20/1000=0.02
逆向文档频率 IDF=log10/10+1=-0.0414
所以 TF-IDF=0.02*(-0.0414)=-8.28e-4。

针对“bayes”，计算 TF-IDF 值：

TF-IDF=0.005*0.5229=2.61e-3。

很明显“bayes”的 TF-IDF 值要大于“this”的 TF-IDF 值。这就说明用“bayes”这个单词做区分比单词“this”要好。

在sklearn中如何计算 TF-IDF值？
直接使用TfidfVectorizer类，有两个构造参数：stop_word和token_pattern。

创建好TfidfVectorizer向量类时，可以使用fit_transform帮我们计算，返回给我们文本矩阵，该矩阵表示每个单词在每个文档中的TF-IDF值。

fit_transform拟合后，可以获得更多TF-IDF属性，比如词汇对应关系（字典类型）和向量IDF值，以及stop_words。

想要计算文档里都有哪些单词，这些单词在不同文档中的TF-IDF的值是多少：

#创建TfidfVectorizer类
from sklearn.feature_extraction.text import TfidfVectorizer
tfidf_vec=TfidfVectorizer()

#创建4个文档的列表
documents=["this is the bayes document","this is the second second moment","and the third one","is this the document"]
tfidf_matrix=tfidf_vec.fit_transform(documents)

#输出所有不重复的词：
print("不重复的词：",tfidf_vec.get_feature_names())

输出：不重复的词： ['and', 'bayes', 'document', 'is', 'moment', 'one', 'second', 'the', 'third', 'this']

#输出每个单词对应的ID值：
print("每个单词的ID：",tfidf_vec.vocabulary_)
输出：每个单词的ID： {'this': 9, 'is': 3, 'the': 7, 'bayes': 1, 'document': 2, 'second': 6, 'moment': 4, 'and': 0, 'third': 8, 'one': 5}

#输出每个单词在文档中的TF-IDF值
print("每个单词的tfidf的值：",tfidf_matrix.toarray())
输出：
每个单词的tfidf的值： [[0.         0.60759891 0.47903796 0.38782252 0.         0.
 -         0.31707032 0.         0.38782252]
 [0.         0.         0.         0.25870773 0.40531566 0.
  0.81063132 0.21151052 0.         0.25870773]
 [0.55280532 0.         0.         0.         0.         0.55280532
 -         0.28847675 0.55280532 0.        ]
 [0.         0.         0.60313701 0.48829139 0.         0.
 -         0.39921021 0.         0.48829139]]

如何对文档进行分类

1、准备阶段：基于分词的数据准备，包括分词、单词权重计算、去掉停用词；

• 对文档进行分词，中英文文档所使用的分词工具不同，英文文档使用最多的是NTLK包，中文中最常用的就是jieba;
• 加载停用词表，需要自己读取停用词表文件，从网上找到中文常用的停用词表放在stop_words.txt，然后利用 Python 的文件读取函数读取文件，保存在 stop_words 数组中。
• 模块 3：计算单词的权重：这里我们用到 sklearn 里的 TfidfVectorizer 类，上面我们介绍过它使用的方法。直接创建 TfidfVectorizer 类，然后使用 fit_transform 方法进行拟合，得到 TF-IDF 特征空间 features，你可以理解为选出来的分词就是特征。我们计算这些特征在文档上的特征向量，得到特征空间 features。

2、分类阶段：应用朴素贝叶斯分类进行分类，首先通过训练集得到朴素贝叶斯分类器，然后将分类器应用于测试集，并与实际结果做对比，最终得到测试集的分类准确率。

• 模块 4：生成朴素贝叶斯分类器:我们将特征训练集的特征空间train_features，以及训练集对应的分类 train_labels 传递给贝叶斯分类器 clf，它会自动生成一个符合特征空间和对应分类的分类器。这里采用的是多项式贝叶斯分类器，其中 alpha 为平滑参数。是为了避免零概率的问题。当 alpha=1 时，使用的是 Laplace 平滑。当 0
• 模块 5：使用生成的分类器做预测:首先我们需要得到测试集的特征矩阵。
  方法是用训练集的分词创建一个 TfidfVectorizer 类，使用同样的stop_words 和 max_df，然后用这个 TfidfVectorizer 类对测试集的内容进行fit_transform 拟合，得到测试集的特征矩阵 test_features。
  模块 6：计算准确率:计算准确率实际上是对分类模型的评估。我们可以调用 sklearn 中的 metrics 包，在 metrics 中提供了 accuracy_score 函数，方便我们对实际结果和预测的结果做对比，给出模型的准确率。
  总结：
  

​