波动方程的行波解(一)| 一维波动方程的通解和初值问题的达朗贝尔(d' Alembert)公式 | 偏微分方程(九)
某些二阶线性偏微分方程,可分解为两个一阶线性偏微分方程,有可能积分求出通解。例如,二阶方程
∂ 2 u ∂ x ∂ y + ∂ u ∂ x = 0 \frac{\partial^2u}{\partial x\partial y}+\frac{\partial u}{\partial x}=0 ∂x∂y∂2u+∂x∂u=0
等价于两个一阶线性偏微分方程
∂ v ∂ x = 0 和 ∂ u ∂ y + u = v \frac{\partial v}{\partial x}=0 \quad 和 \frac{\partial u}{\partial y}+u=v ∂x∂v=0和∂y∂u+u=v
第一个方程对x积分,得 v ( x , y ) = f ( y ) v(x,y)=f(y) v(x,y)=f(y), f ( y ) f(y) f(y)为任意C函数。第二个方程对y积分,解得 u ( x , y ) = e − y g ( y ) + h ( y ) u(x,y)=e^{-y}g(y)+h(y) u(x,y)=e−yg(y)+h(y), g ( y ) g(y) g(y)是任意 C 1 C^1 C1函数, h ( y ) = e − y ∫ f ( y ) e y d y h(y)=e^{-y}\int f(y)e^ydy h(y)=e−y∫f(y)eydy也是任意 C 1 C^1 C1函数。
接下来用此分解降阶的方法求出一维波动方程的通解(行波解),并通过若干例子介绍由通解确定特解的方法,并从物理上对解的行波特点作简要分析。
1.4.1 一维波动方程的通解和初值问题的达朗贝尔(d’ Alembert)公式
一维波动方程
∂ 2 u ∂ t 2 = a 2 ∂ 2 u ∂ x 2 (1) \frac{\partial^2 u}{\partial t^2}=a^2\frac{\partial^2u}{\partial x^2} \tag{1} ∂t2∂2u=a2∂x2∂2u(1)
在 a > 0 a>0 a>0为常数时可分解为
( ∂ ∂ t + a ∂ ∂ x ) ( ∂ ∂ t − a ∂ ∂ x ) u = 0 (\frac{\partial}{\partial t}+a\frac{\partial}{\partial x})(\frac{\partial}{\partial t}-a\frac{\partial}{\partial x})u=0 (∂t∂+a∂x∂)(∂t∂−a∂x∂)u=0
等价于两个一阶线性偏微分方程的方程组
{ ∂ v ∂ t + a ∂ v ∂ x = 0 ∂ u ∂ t − a ∂ u ∂ x = v \begin{cases} \frac{\partial v}{\partial t}+a\frac{\partial v}{\partial x}=0 \\ \frac{\partial u}{\partial t}-a\frac{\partial u}{\partial x}=v \end{cases} {∂t∂v+a∂x∂v=0∂t∂u−a∂x∂u=v
这两个方程各有一族独立的特征线,分别是
x − a t = c 1 , x + a t = c 2 x-at=c_1, \quad x+at=c_2 x−at=c1,x+at=c2
引入新的自变量
ξ = x − a t , η = x + a t \xi=x-at,\quad \eta=x+at ξ=x−at,η=x+at
利用链式法则, u = u ( t , x ) u=u(t,x) u=u(t,x)的方程(1)变为 u = u ( ξ , η ) u=u(\xi,\eta) u=u(ξ,η)的新方程
∂ 2 u ∂ η ∂ ξ = 0 \frac{\partial^2u}{\partial \eta \partial \xi}=0 ∂η∂ξ∂2u=0
相继对 η , ξ \eta,\xi η,ξ积分,代回源自变量,得一维波动方程(1)的通解
u = f ( ξ ) + g ( η ) = f ( x − a t ) + g ( x + a t ) (2) u=f(\xi)+g(\eta)=f(x-at)+g(x+at) \tag{2} u=f(ξ)+g(η)=f(x−at)+g(x+at)(2)
其中, f , g f,g f,g是任意一元 C 2 C^2 C2函数。
可见,一维波动方程的解是由速度同为 a a a的两列反向行进的波组成,称为行波解。其中, f ( x − a t ) f(x-at) f(x−at)为右行波, g ( x + a t ) g(x+at) g(x+at)为左行波,波形 f ( ξ ) , g ( η ) f(\xi),g(\eta) f(ξ),g(η)则需由定解条件确定。
例1:无限长弦的自由振动
{ ∂ 2 u ∂ t 2 = a 2 ∂ 2 u ∂ x 2 , t > 0 , − ∞ < x < + ∞ u ∣ t = 0 = φ ( x ) , ∂ u ∂ t ∣ t = 0 = ψ ( x ) (3) \begin{cases} \frac{\partial^2 u}{\partial t^2}=a^2\frac{\partial^2u}{\partial x^2},\quad t>0,-\infty
解:讲初始条件代入通解(2),得
u ∣ t = 0 = f ( x ) + g ( x ) = φ ( x ) ∂ u ∂ t ∣ t = 0 = − a f ′ ( x ) + a g ′ ( x ) = ψ ( x ) u|_{t=0}=f(x)+g(x)=\varphi(x) \\ \frac{\partial u}{\partial t}|_{t=0}=-af'(x)+ag'(x)=\psi(x) u∣t=0=f(x)+g(x)=φ(x)∂t∂u∣t=0=−af′(x)+ag′(x)=ψ(x)
积分第二式,得
− f ( x ) + g ( x ) = 1 a ∫ 0 x ψ ( ξ ) d ξ + c -f(x)+g(x)=\frac{1}{a}\int_0^x\psi(\xi)d\xi+c −f(x)+g(x)=a1∫0xψ(ξ)dξ+c
解 f ( x ) , g ( x ) f(x),g(x) f(x),g(x)的联立方程组,得
f ( x ) = 1 2 [ φ ( x ) − 1 a ∫ 0 x ψ ( ξ ) d ξ − c ] g ( x ) = 1 2 [ φ ( x ) + 1 a ∫ 0 x ψ ( ξ ) d ξ + c ] f(x)=\frac{1}{2}[\varphi(x)-\frac{1}{a}\int_0^x\psi(\xi)d\xi-c] \\ g(x)=\frac{1}{2}[\varphi(x)+\frac{1}{a}\int_0^x\psi(\xi)d\xi+c] f(x)=21[φ(x)−a1∫0xψ(ξ)dξ−c]g(x)=21[φ(x)+a1∫0xψ(ξ)dξ+c]
从而,初值问题(3)式的解必有形式
u ( t , x ) = 1 2 [ φ ( x − a t ) + φ ( x + a t ) ] + 1 2 a ∫ x − a t x + a t ψ ( ξ ) d ξ u(t,x)=\frac{1}{2}[\varphi(x-at)+\varphi(x+at)]+\frac{1}{2a}\int_{x-at}^{x+at}\psi(\xi)d\xi u(t,x)=21[φ(x−at)+φ(x+at)]+2a1∫x−atx+atψ(ξ)dξ
称为达朗贝尔公式。
不难直接验证,当初始条件 φ ( x ) ∈ C 2 ( R ) , ψ ( x ) ∈ C 1 ( R ) \varphi(x)\in C^2(R),\psi(x)\in C^1(R) φ(x)∈C2(R),ψ(x)∈C1(R)时达朗贝尔公式给出的u确是初值问题(3)的古典解。因此,达朗贝尔公式是初值问题(3)式的唯一解。
又设(3)式中的初始条件有微小变化, u ∣ t = 0 = φ ( x ) + h 1 ( x ) , ∂ u ∂ ∣ t = 0 = ψ ( x ) + h 2 ( x ) u|_{t=0}=\varphi(x)+h_1(x), \frac{\partial u}{\partial}|_{t=0}=\psi(x)+h_2(x) u∣t=0=φ(x)+h1(x),∂∂u∣t=0=ψ(x)+h2(x),其中, ∣ h j ( x ) ∣ ≤ δ ( j = 1 , 2 ) |h_j(x)|\leq \delta(j=1,2) ∣hj(x)∣≤δ(j=1,2)。记在此初始条件下得到的达朗贝尔解为 u ^ ( t , x ) \hat u(t,x) u^(t,x),则
∣ u ^ ( t , x ) − u ( t , x ) ∣ = ∣ 1 2 ( h 1 ( x − a t ) + h 1 ( x + a t ) ) + 1 2 a ∫ x − a t x + a t h 2 ( ξ ) d ξ ∣ ≤ ( 1 + t ) δ |\hat u(t,x)-u(t,x)|=|\frac{1}{2}(h_1(x-at)+h_1(x+at))+\frac{1}{2a}\int_{x-at}^{x+at}h_2(\xi)d\xi|\leq (1+t)\delta ∣u^(t,x)−u(t,x)∣=∣21(h1(x−at)+h1(x+at))+2a1∫x−atx+ath2(ξ)dξ∣≤(1+t)δ
故在任意有限时间范围内,只要初始条件的误差 δ \delta δ足够小,解的误差可控制在一定,达朗贝尔公式给出的是稳定解。由此可见,一维波动方程的初值问题是适定的。
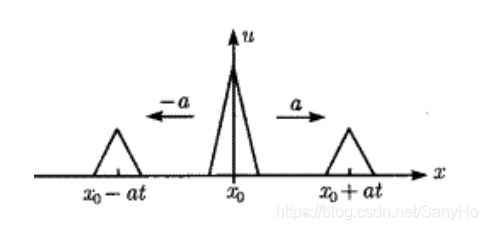
达朗贝尔公式清楚反映了初始扰动在弦上的传播过程。初位移 φ ( x ) \varphi(x) φ(x)以 1 2 φ ( x ) \frac{1}{2}\varphi(x) 21φ(x)的波形,以速度 a a a向弦的两边传播。如下图
而且x点在t时刻由初位移引起的位移 1 2 [ φ ( x − a t ) + φ ( x + a t ) ] \frac{1}{2}[\varphi(x-at)+\varphi(x+at)] 21[φ(x−at)+φ(x+at)]仅取决于x轴上 x − a t x-at x−at和 x + a t x+at x+at两点的初位移。而初速度的影响稍见复杂,是关于x轴对称的两个波形 1 2 a ∫ 0 x ψ ( ξ ) d ξ \frac{1}{2a}\int_0^x\psi(\xi)d\xi 2a1∫0xψ(ξ)dξ和 − 1 2 a ∫ 0 x ψ ( ξ ) d ξ -\frac{1}{2a}\int_0^x\psi(\xi)d\xi −2a1∫0xψ(ξ)dξ分别以速度 a a a向左、右传播,x点他时刻由初速度引起的位移 1 2 a ∫ x − a t x + a t ψ ( ξ ) d ξ \frac{1}{2a}\int_{x-at}^{x+at}\psi(\xi)d\xi 2a1∫x−atx+atψ(ξ)dξ是一种累积效应,取决于初速度在 [ x − a t , x + a t ] [x-at,x+at] [x−at,x+at]整个区间内的值。称x轴上区间 [ x − a t , x + a t ] [x-at,x+at] [x−at,x+at]为点 ( x , t ) (x,t) (x,t)的依赖区间,可由经过 ( x , t ) (x,t) (x,t)的两条特征线确定。
反过来看,初始时刻 t = 0 t=0 t=0, x 0 x_0 x0点的初位移 φ ( x 0 ) \varphi(x_0) φ(x0)经过时间t,仅沿过 x 0 x_0 x0点的两条特征线传播到 x 0 − a t x_0-at x0−at和 x 0 + a t x_0+at x0+at两点,而 x 0 x_0 x0点的初速度 ψ ( x 0 ) \psi(x_0) ψ(x0)则影响到区间 [ x 0 − a t , x 0 + a t ] [x_0-at,x_0+at] [x0−at,x0+at]中的所有点,是一种“弥漫作用”。
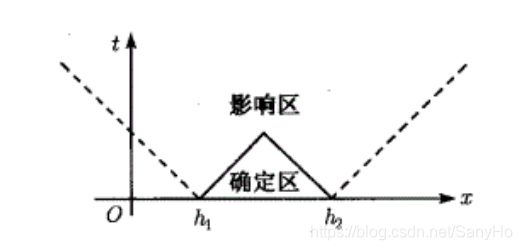
若初始扰动发生在区间 [ h 1 , h 2 ] [h_1,h_2] [h1,h2]上,则可唯一确定过左、右端点的右、左行特征线所围的特征三角形区域上的 u ( t , x ) u(t,x) u(t,x),称此三角形为 [ h 1 , h 2 ] [h_1,h_2] [h1,h2]上初始扰动的确定区域。而过左、右两端的左、右行特征线所围的无界特征形内各点的 u ( t , x ) u(t,x) u(t,x)都受到 [ h 1 , h 2 ] [h_1,h_2] [h1,h2]上初始扰动的影响,称此梯形为初始扰动的影响区域,如下图
例2:特征边值问题(Goursat问题)
{ ∂ 2 u ∂ t 2 = a 2 ∂ 2 u ∂ x 2 u ∣ x − a t = 0 = φ ( x ) , u ∣ x + a t = 0 = ψ ( x ) , φ ( 0 ) = ψ ( 0 ) \begin{cases} \frac{\partial^2 u}{\partial t^2}=a^2\frac{\partial^2 u}{\partial x^2} \\ u|_{x-at=0}=\varphi(x),\quad u|_{x+at=0}=\psi(x), \quad \varphi(0)=\psi(0) \end{cases} {∂t2∂2u=a2∂x2∂2uu∣x−at=0=φ(x),u∣x+at=0=ψ(x),φ(0)=ψ(0)
解:将定解条件代入通解 u = f ( x − a t ) + g ( x + a t ) u=f(x-at)+g(x+at) u=f(x−at)+g(x+at),由
u ∣ x − a t = 0 = f ( 0 ) + g ( 2 x ) = φ ( x ) , u ∣ x + a t = 0 = f ( 2 x ) + g ( 0 ) = ψ ( x ) u|_{x-at=0}=f(0)+g(2x)=\varphi(x), \\ u|_{x+at=0}=f(2x)+g(0)=\psi(x) u∣x−at=0=f(0)+g(2x)=φ(x),u∣x+at=0=f(2x)+g(0)=ψ(x)
解得
f ( ξ ) = ψ ( ξ 2 ) − g ( 0 ) g ( ξ ) = φ ( ξ 2 ) − f ( 0 ) f(\xi)=\psi(\frac{\xi}{2})-g(0) \\ g(\xi)=\varphi(\frac{\xi}{2})-f(0) f(ξ)=ψ(2ξ)−g(0)g(ξ)=φ(2ξ)−f(0)
有
f ( 0 ) + g ( 0 ) = 1 2 [ φ ( 0 ) + ψ ( 0 ) ] f(0)+g(0)=\frac{1}{2}[\varphi(0)+\psi(0)] f(0)+g(0)=21[φ(0)+ψ(0)]
故
u = φ ( x + a t 2 ) + ψ ( x − a t 2 ) − φ ( 0 ) u=\varphi(\frac{x+at}{2})+\psi(\frac{x-at}{2})-\varphi(0) u=φ(2x+at)+ψ(2x−at)−φ(0)
由于两条不同族的特征线上给出边界条件,对任意 φ ( x ) , ψ ( x ) \varphi(x),\psi(x) φ(x),ψ(x),只要 φ ( 0 ) = ψ ( 0 ) \varphi(0)=\psi(0) φ(0)=ψ(0),解都存在、唯一。